6 Квантовая физика. Физика атома 2 Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
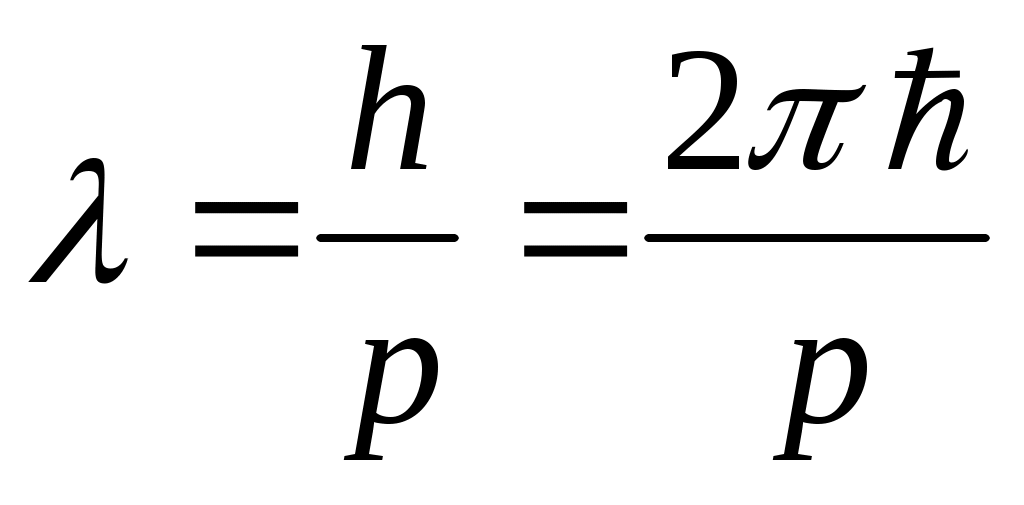 – формула де Бройля. – формула де Бройля.
Принцип неопределенности Гейзенберга: произведение неопределенностей двух канонически сопряженных величин не может быть по порядку величины меньше постоянной Планка 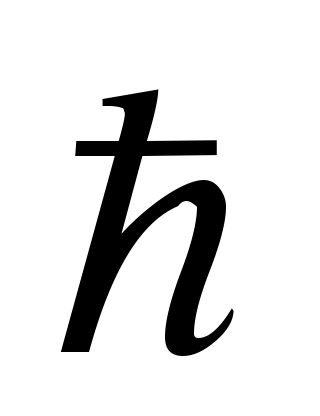 . .
Соотношения неопределённостей Гейзенберга:
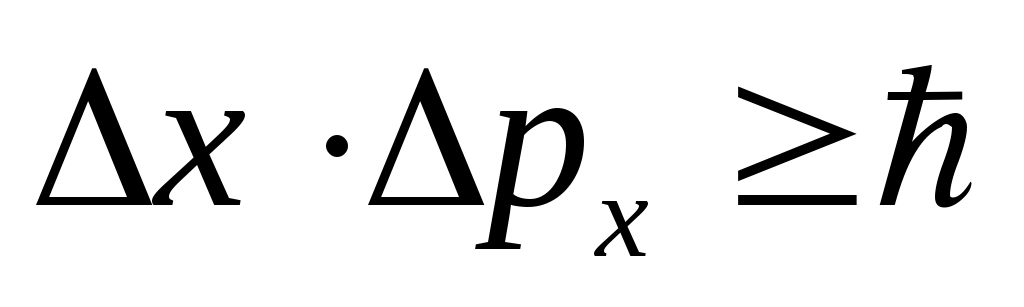 , , 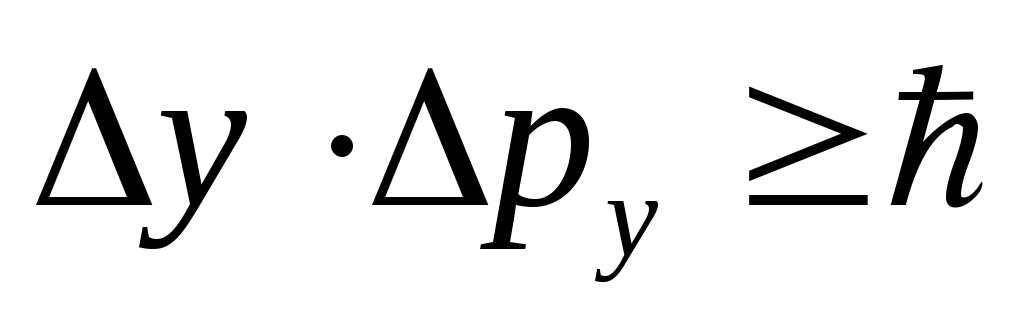 , , 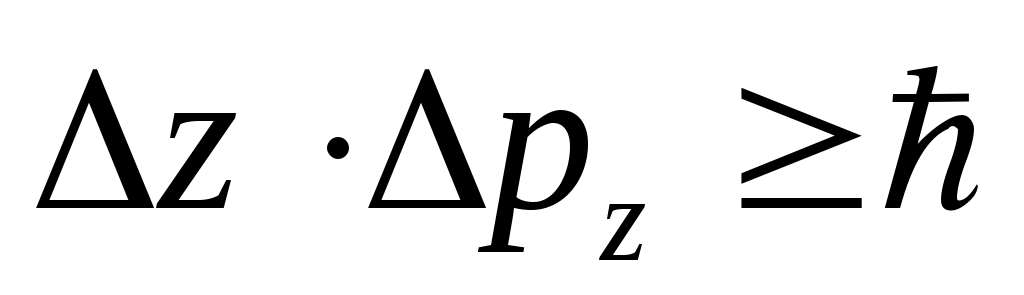 , , 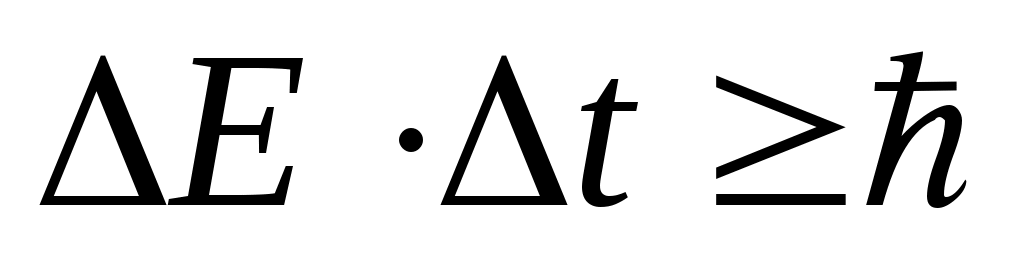 . .
Ф6.2.1-1
Длина волны де Бройля выражается по следующей формуле: 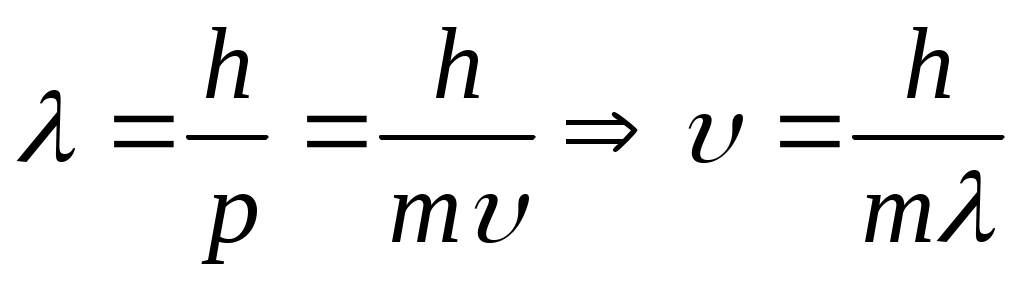 , где h – постоянная Планка ( , где h – постоянная Планка (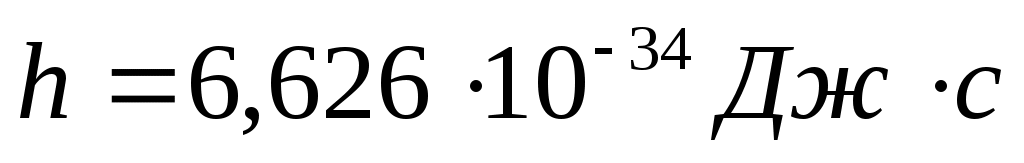 ), m – масса частицы, υ – скорость частицы. ), m – масса частицы, υ – скорость частицы.
Если длины волн де Бройля равны, то зависимость скорости выглядит так 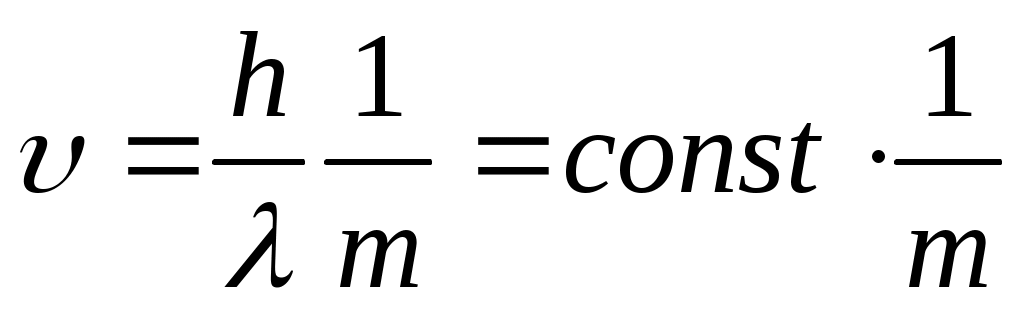 (обратно-пропорциональная зависимость), значит, чем больше масса, тем меньше скорость. Из предложенных частиц большей массой обладает α – частица. (обратно-пропорциональная зависимость), значит, чем больше масса, тем меньше скорость. Из предложенных частиц большей массой обладает α – частица.
Ответ: 3
Ф6.2.1-2
Длина волны де Бройля частицы уменьшилась вдвое. Скорость этой частицы …
|
1: увеличилась в 4 раза
2: уменьшилась в 4 раза
3: не изменилась
4: уменьшилась вдвое
5: увеличилась вдвое*
|
Длина волны де Бройля выражается по следующей формуле: 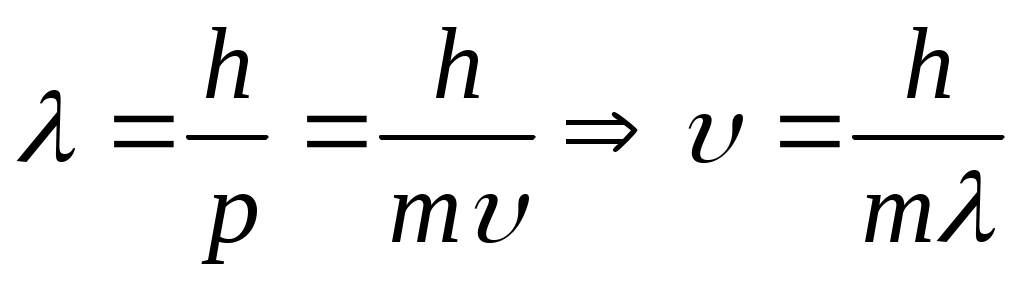 , где h – постоянная Планка ( , где h – постоянная Планка (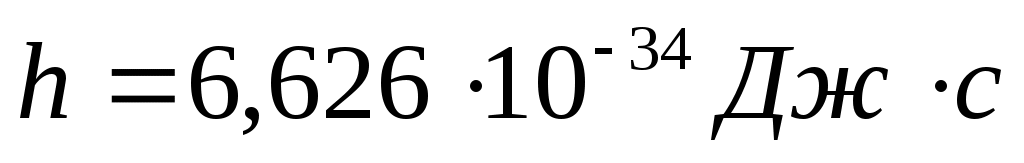 ), m – масса частицы, υ – скорость частицы. ), m – масса частицы, υ – скорость частицы.
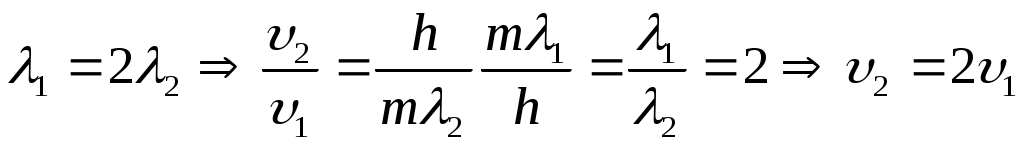 . .
Ответ: 5
Ф6.2.1-3
Если протон и нейтрон двигаются с одинаковыми скоростями, то отношения их длин волн де Бройля λp/λn равно …
|
1: 2
2: 1/2
3: 1*
4: 4
|
Длина волны де Бройля выражается по следующей формуле: 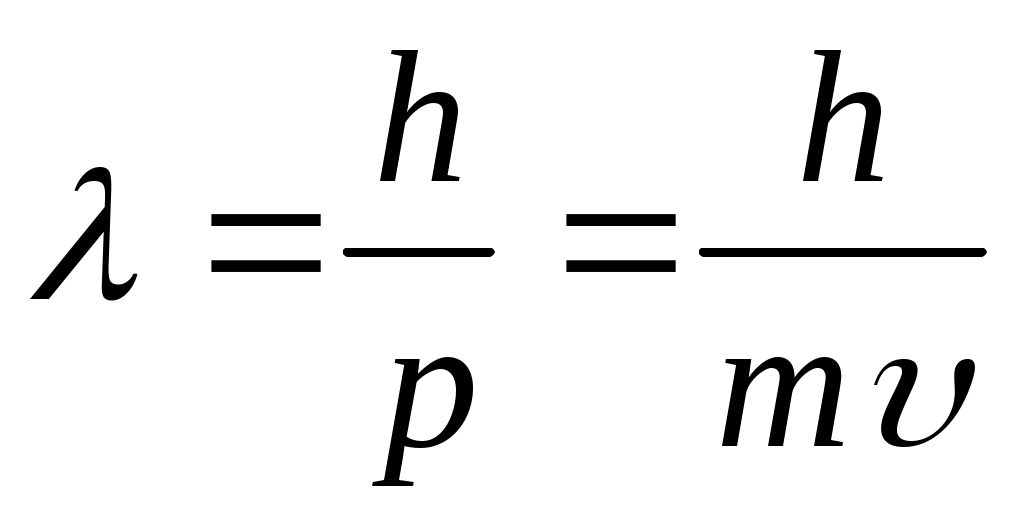 , где h – постоянная Планка ( , где h – постоянная Планка (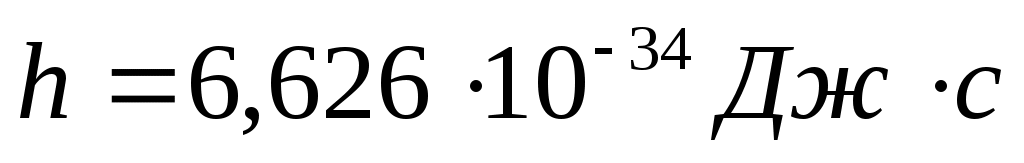 ), m – масса частицы, υ – скорость частицы. Масса протона незначительно отличается от массы нейтрона, т.е. ), m – масса частицы, υ – скорость частицы. Масса протона незначительно отличается от массы нейтрона, т.е. 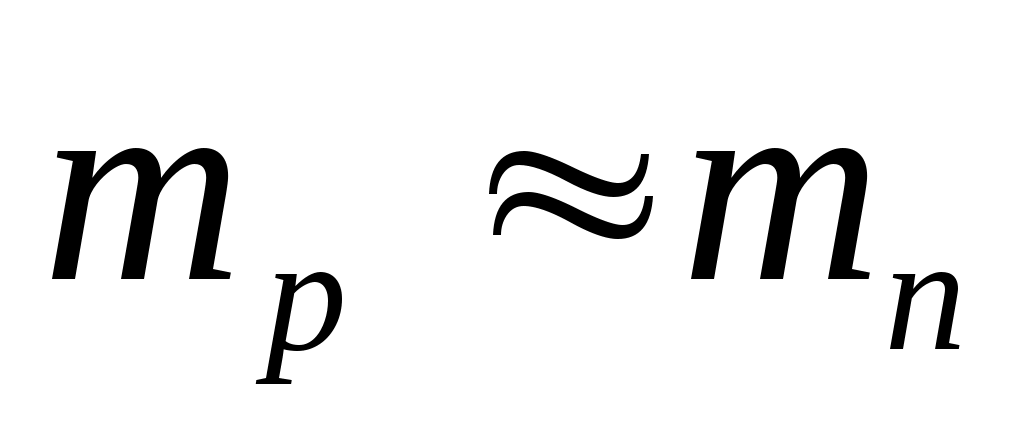 , скорости равны , скорости равны 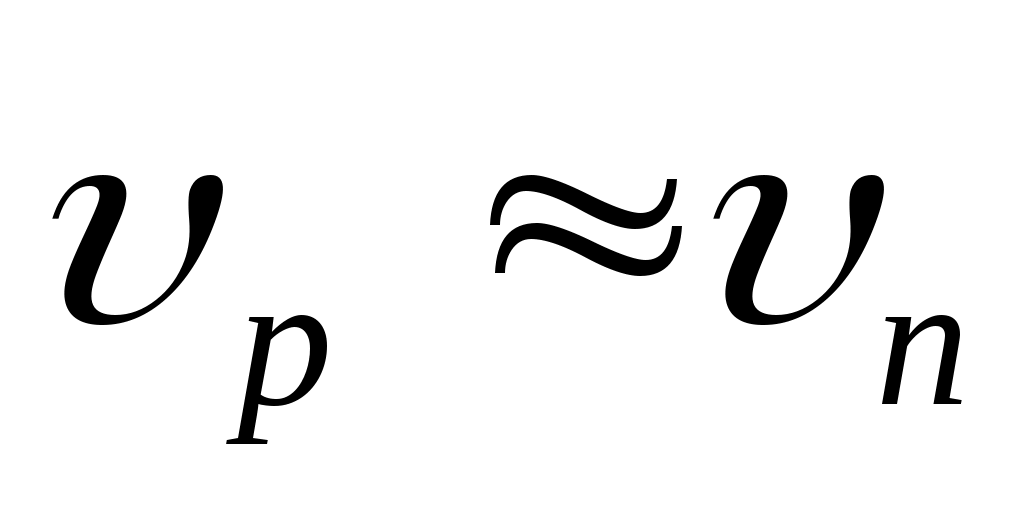 . Поэтому . Поэтому 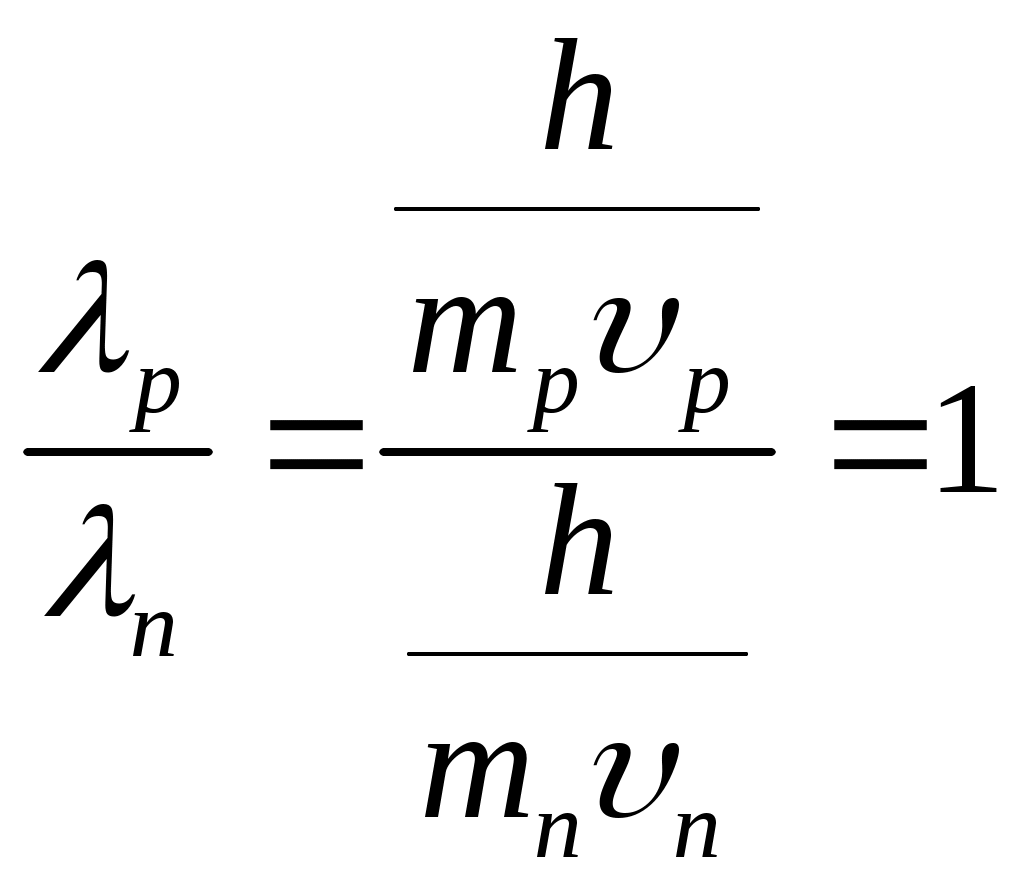 . .
Ответ: 3
Ф6.2.1-4
Если протон и α-частица двигаются с одинаковыми скоростями, то отношения их длин волн де Бройля 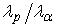 равно … равно …
|
1: 4*
2: 1/2
3: 2
4: 1
|
Длина волны де Бройля выражается по следующей формуле: 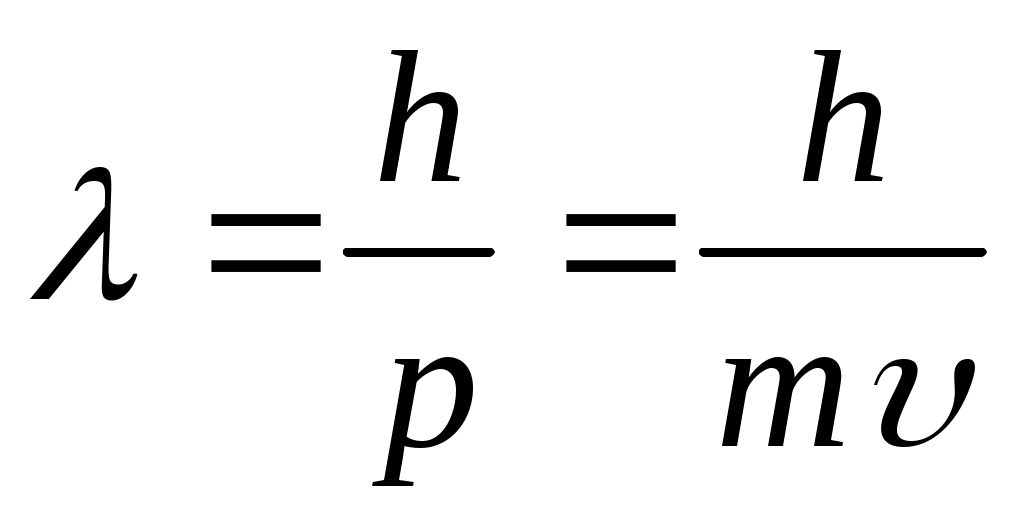 , где h – постоянная Планка ( , где h – постоянная Планка (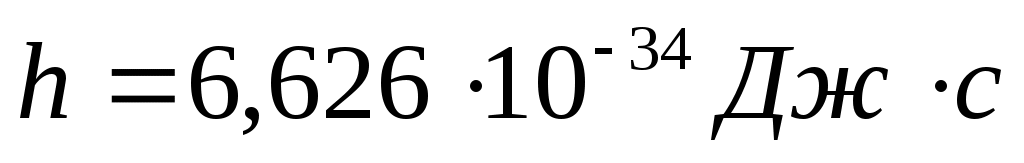 ), m – масса частицы, υ – скорость частицы. Масса протона ), m – масса частицы, υ – скорость частицы. Масса протона 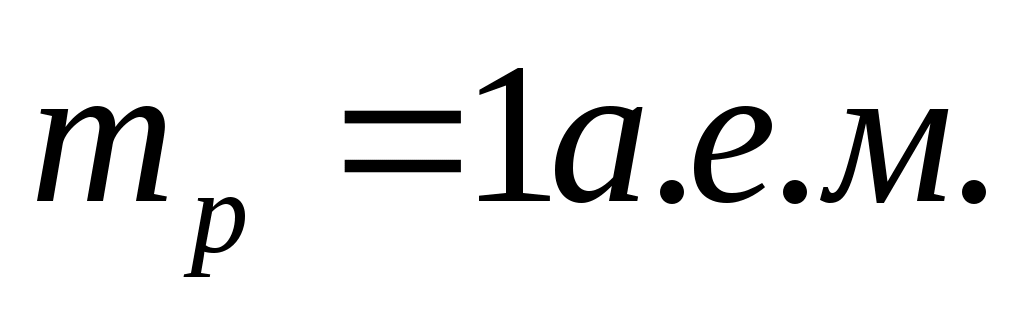 , масса нейтрона , масса нейтрона 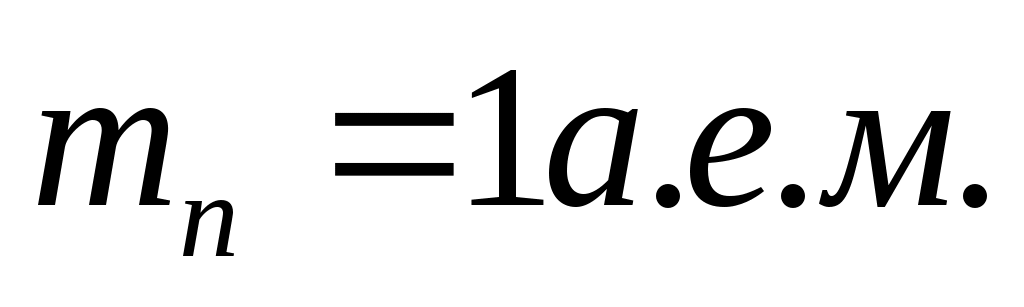 , масса α-частицы , масса α-частицы 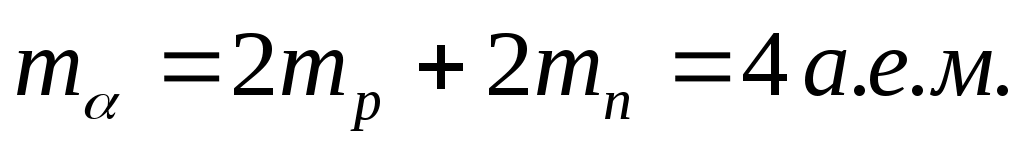 скорости равны скорости равны 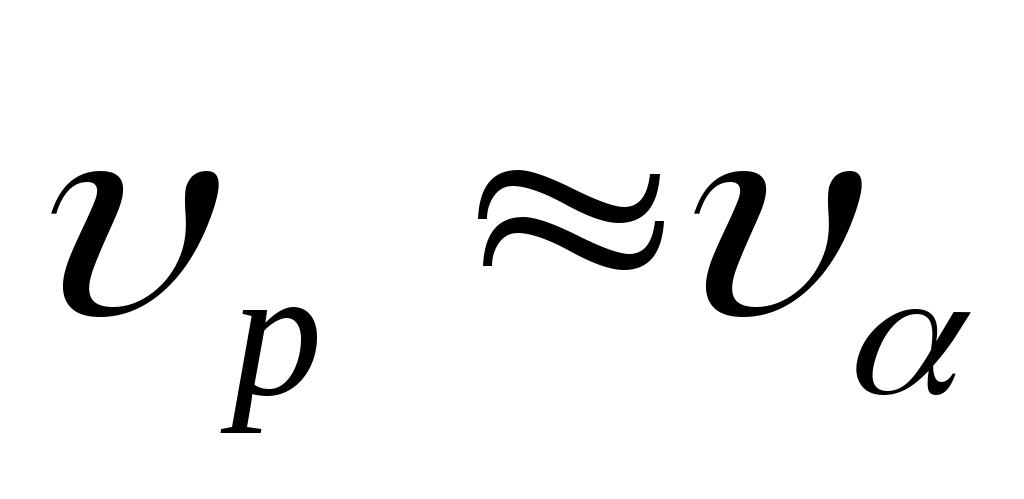 . Поэтому . Поэтому 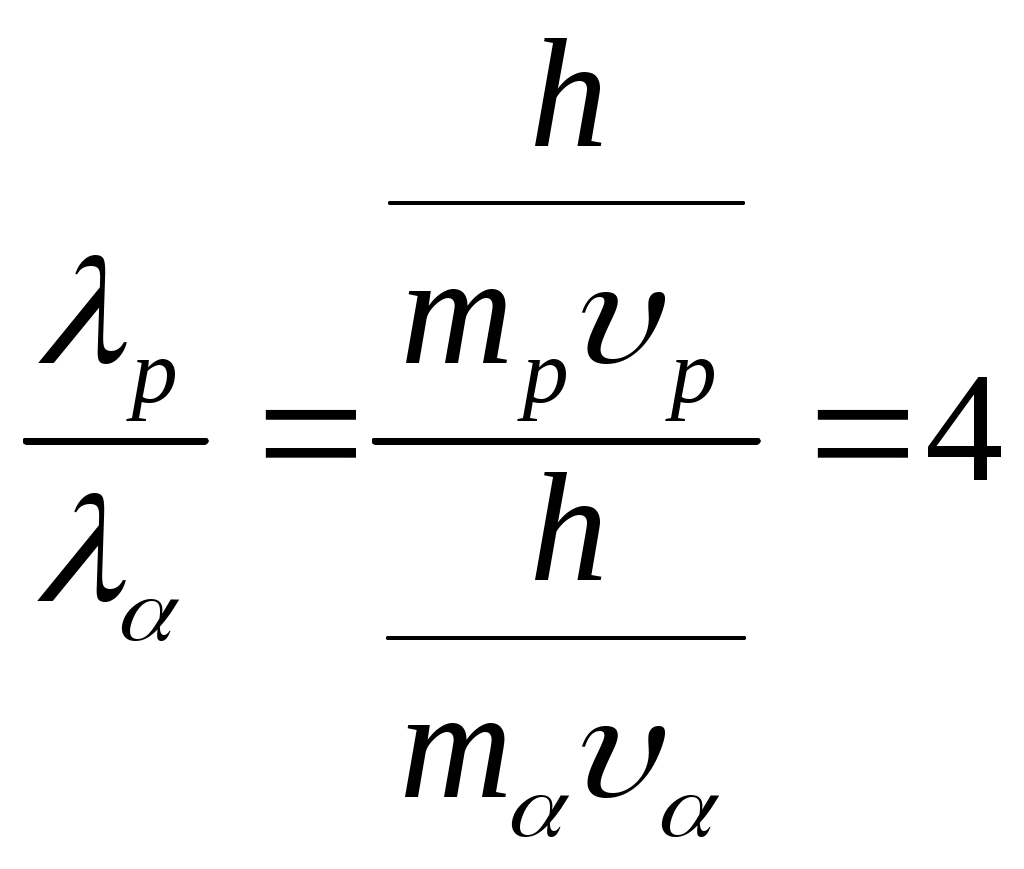 . .
Ответ: 1
Ф6.2.1-5
Если α-частица и нейтрон двигаются с одинаковыми скоростями, то отношения их длин волн де Бройля 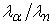 равно … равно …
|
1: ¼*
2: 1/2
3: 2
4: 4
|
Длина волны де Бройля выражается по следующей формуле: 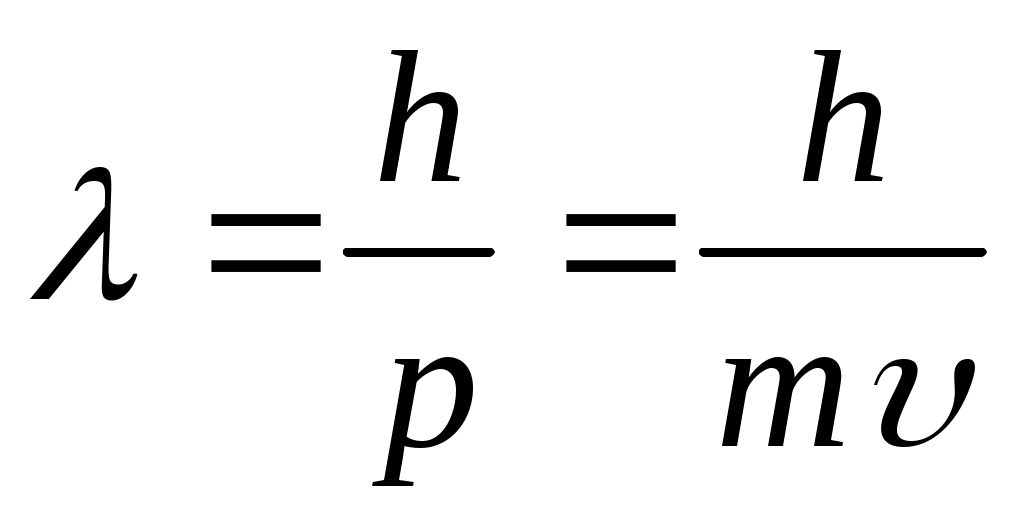 , где h – постоянная Планка ( , где h – постоянная Планка (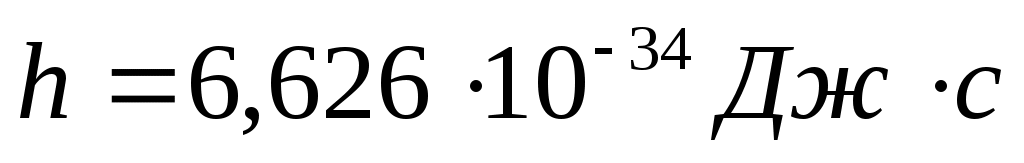 ), m – масса частицы, υ – скорость частицы. Масса нейтрона ), m – масса частицы, υ – скорость частицы. Масса нейтрона 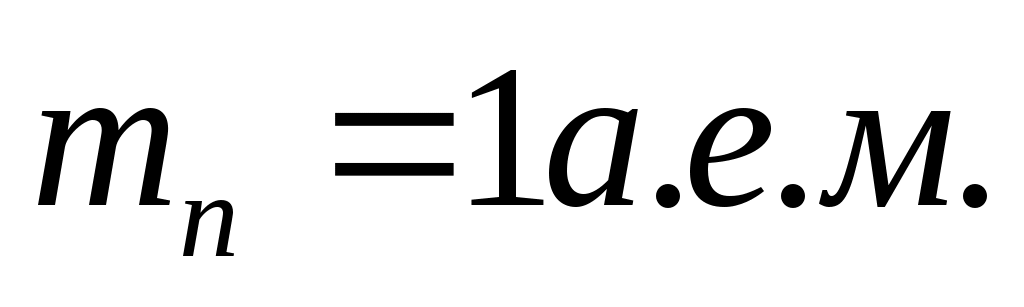 , масса протона , масса протона 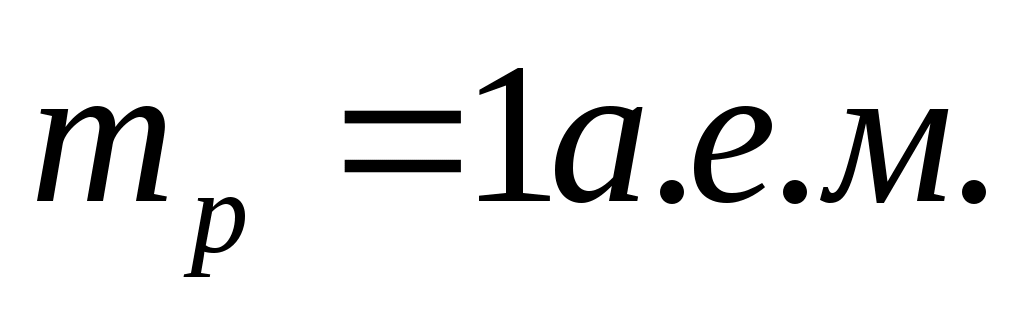 , масса α-частицы , масса α-частицы 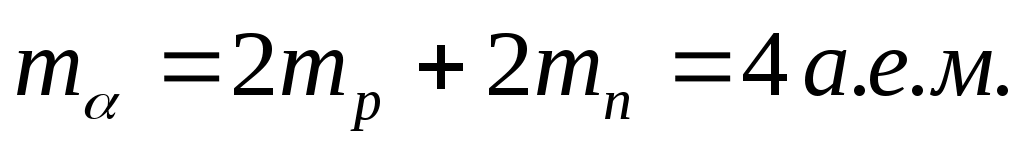 скорости равны скорости равны 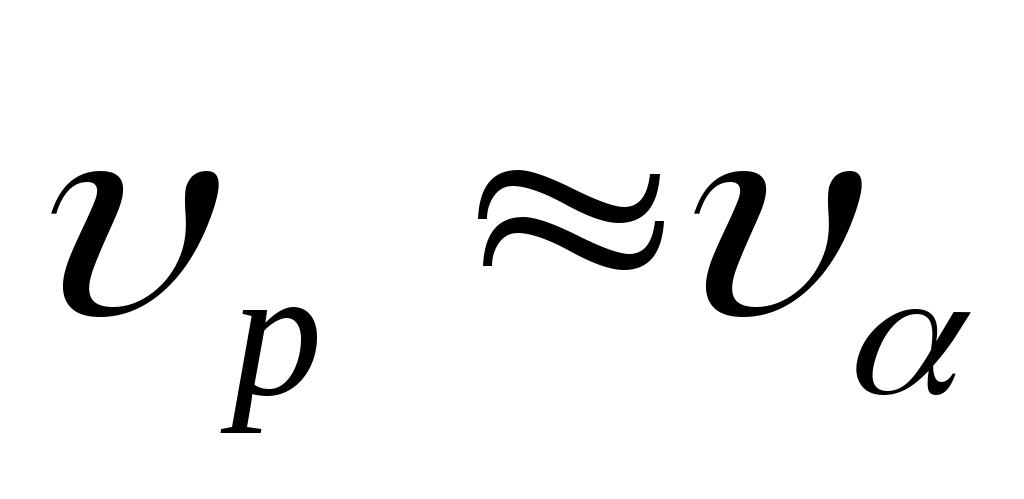 . Поэтому . Поэтому 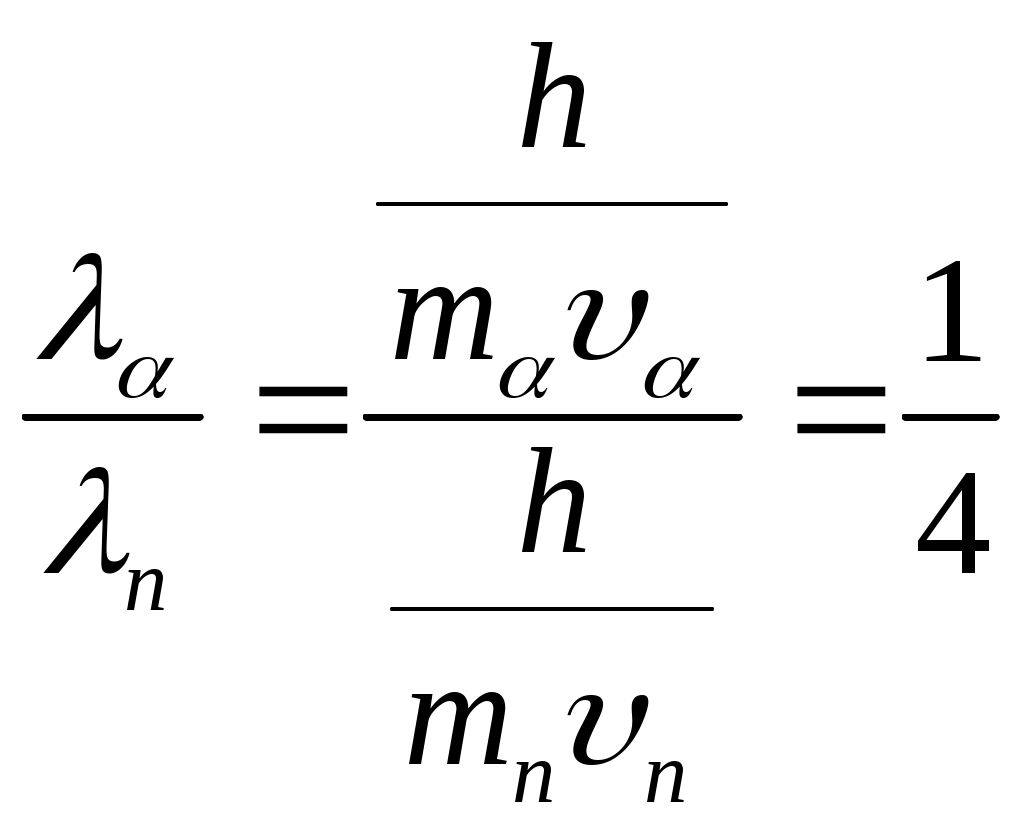 . .
Ответ: 1
Ф6.2.1-6
Если α-частица и протон двигаются с одинаковыми скоростями, то отношения их длин волн де Бройля 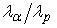 равно … равно …
|
1:1/4*
2:1/2
3:2
4:4
|
Длина волны де Бройля выражается по следующей формуле: 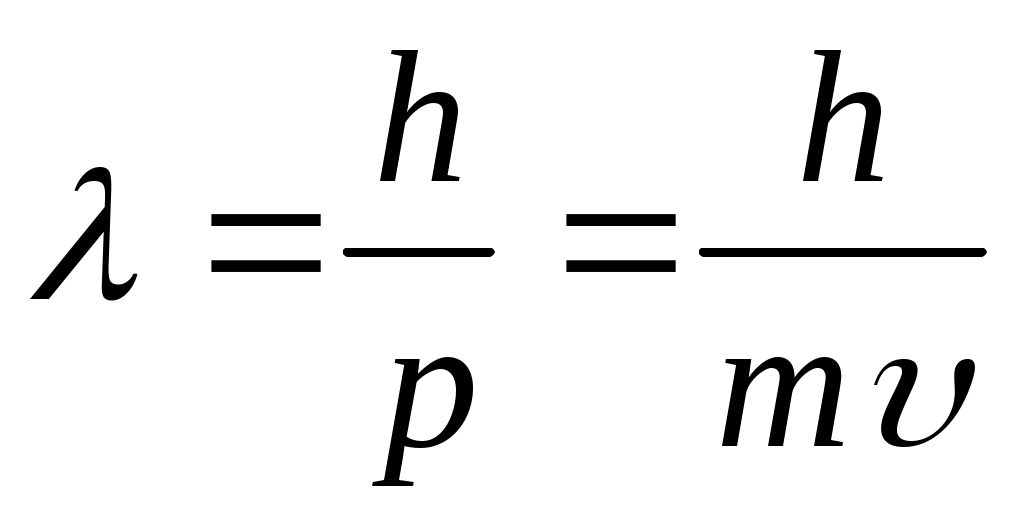 , где h – постоянная Планка ( , где h – постоянная Планка (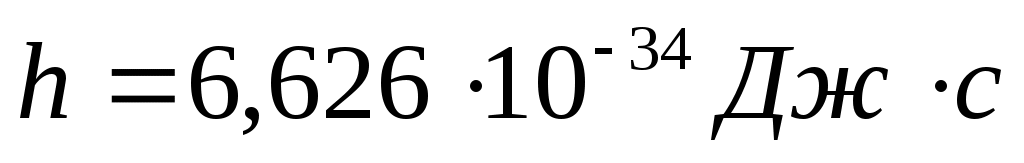 ), m – масса частицы, υ – скорость частицы. Масса протона ), m – масса частицы, υ – скорость частицы. Масса протона 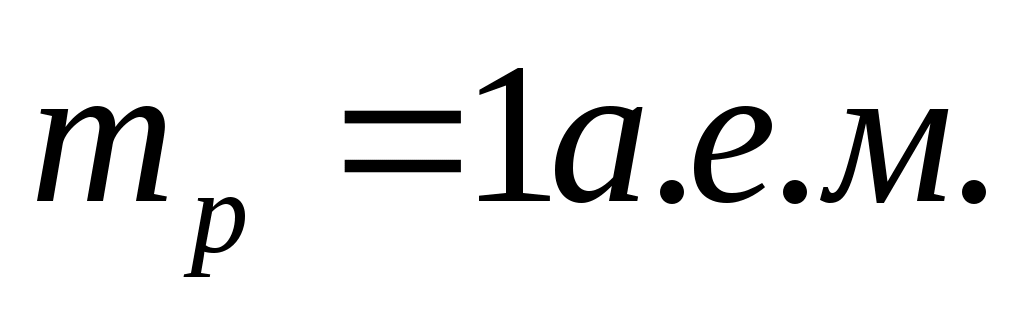 , масса нейтрона , масса нейтрона 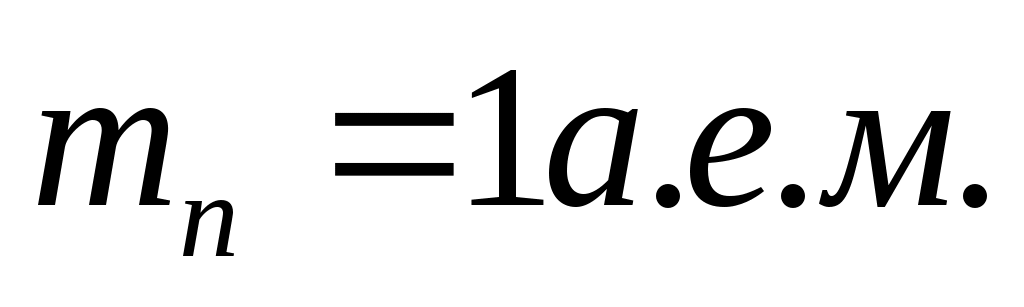 , масса α-частицы , масса α-частицы 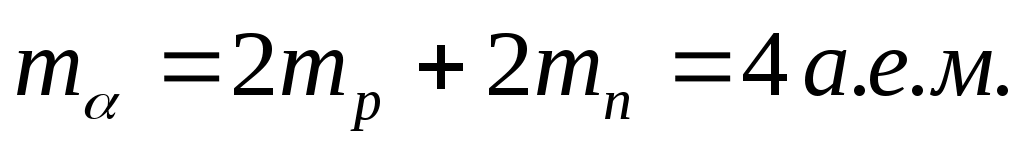 скорости равны скорости равны 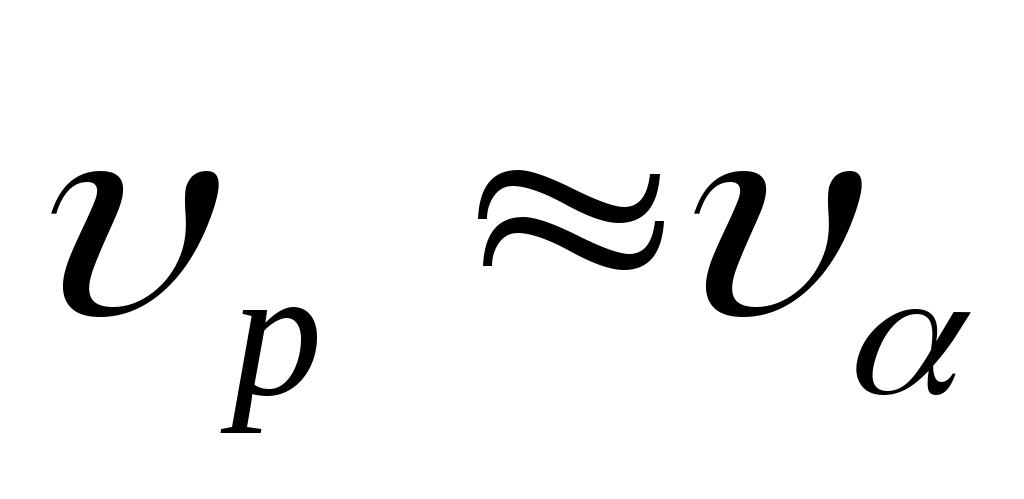 . Поэтому . Поэтому 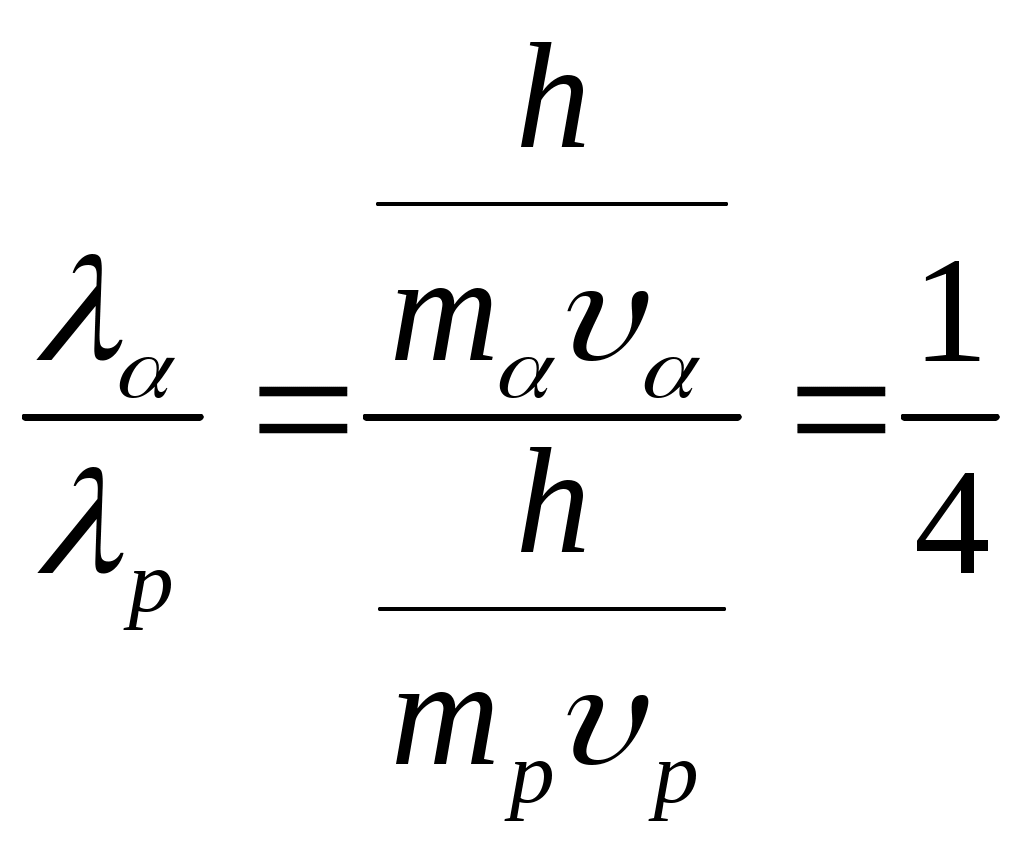 . .
Ответ: 1
Ф6.2.1-7
Если нейтрон и α-частица двигаются с одинаковыми скоростями, то отношения их длин волн де Бройля 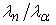 равно … равно …
|
1: 4*
2: 1/2
3: 2
4: 1/4
|
Длина волны де Бройля выражается по следующей формуле: 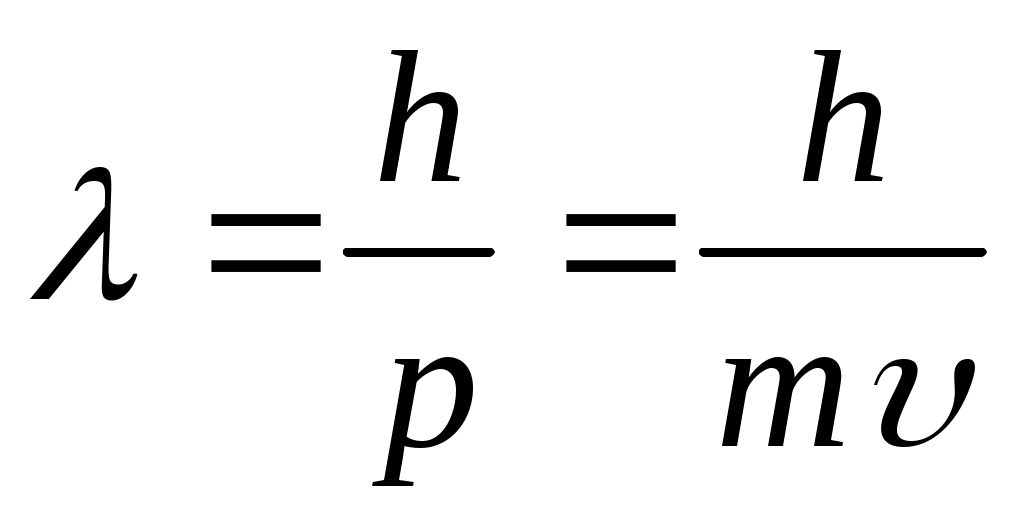 , где h – постоянная Планка ( , где h – постоянная Планка (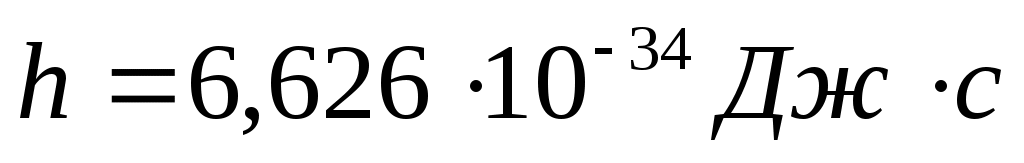 ), m – масса частицы, υ – скорость частицы. Масса нейтрона ), m – масса частицы, υ – скорость частицы. Масса нейтрона 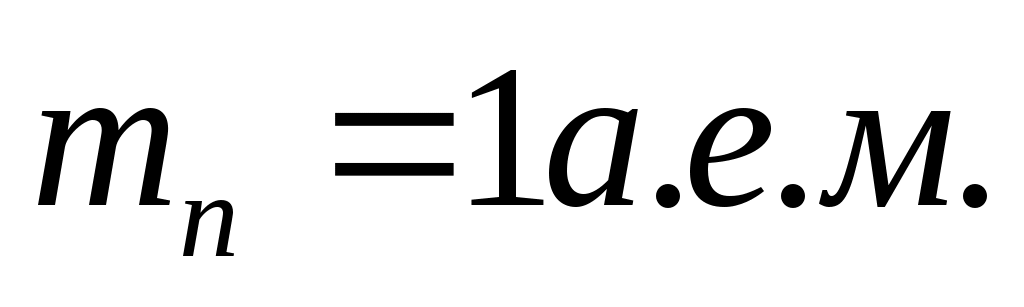 , масса протона , масса протона 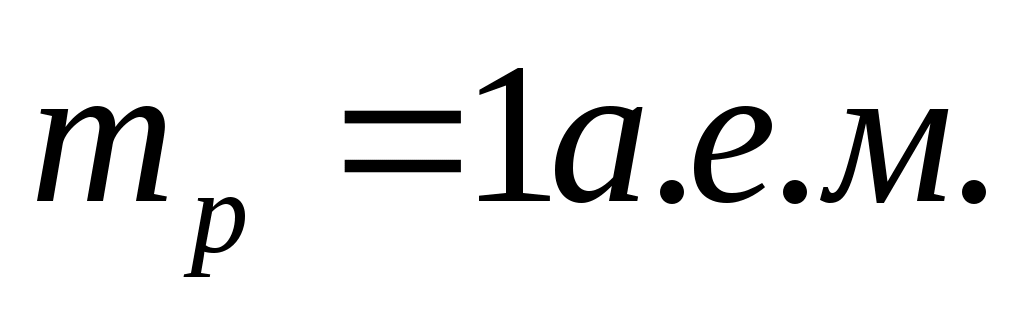 , масса α-частицы , масса α-частицы 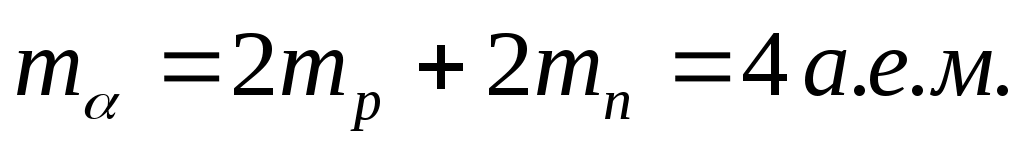 скорости равны скорости равны 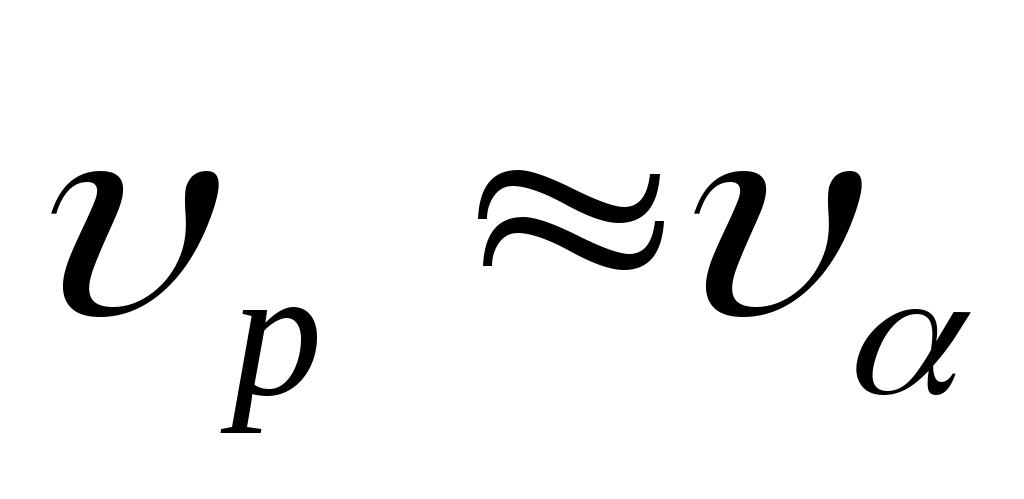 . Поэтому . Поэтому 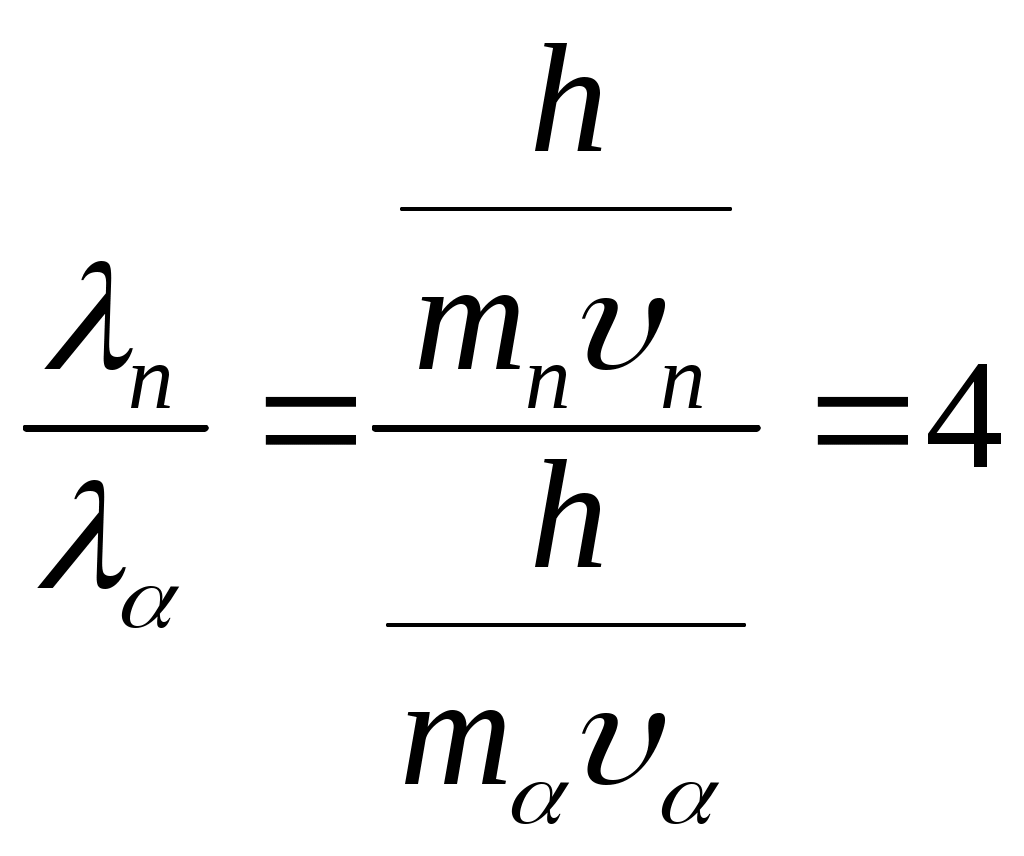 . .
Ответ: 1
Ф6.2.1-8
Де Бройль обобщил соотношение 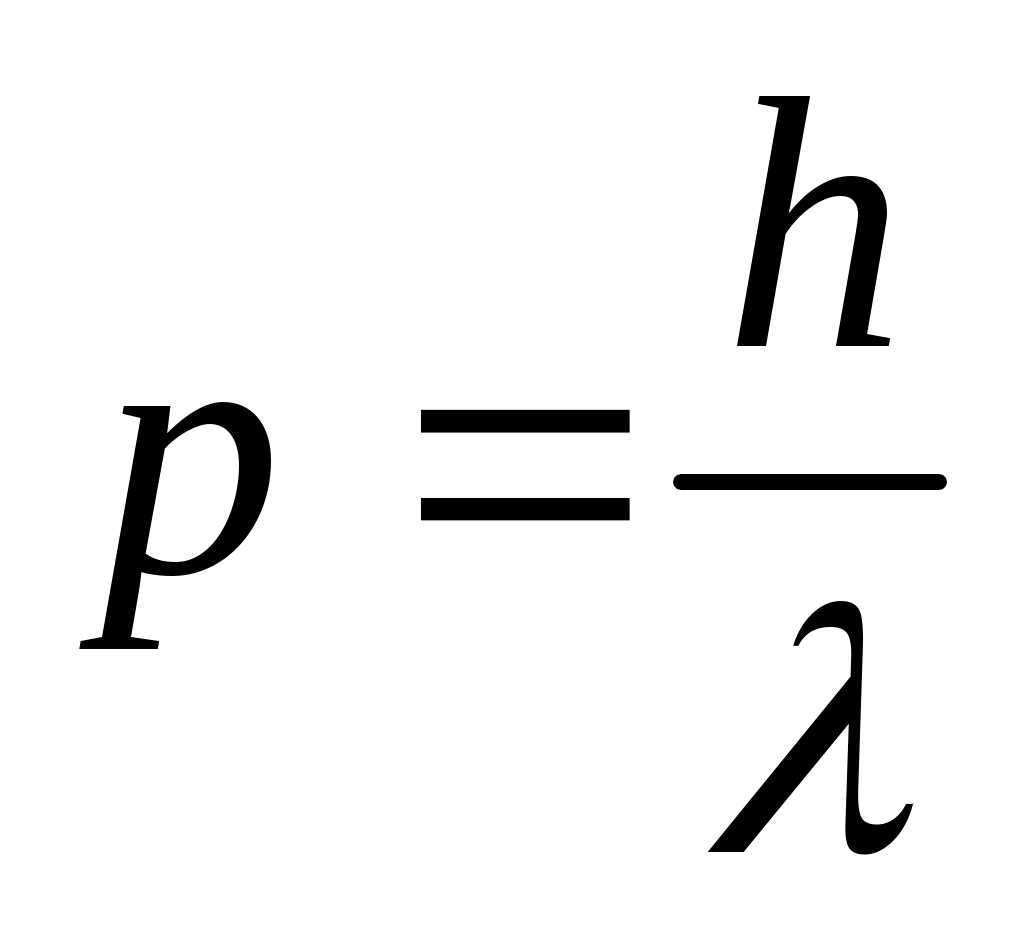 для фотона на любые волновые процессы, связанные с частицами, импульс которых равен р. Тогда, если скорость частиц одинакова, то наименьшей длиной волны обладают … для фотона на любые волновые процессы, связанные с частицами, импульс которых равен р. Тогда, если скорость частиц одинакова, то наименьшей длиной волны обладают …
|
1: нейтроны
2: электроны
3: α-частицы*
4: протоны
|
Длина волны де Бройля выражается по следующей формуле: 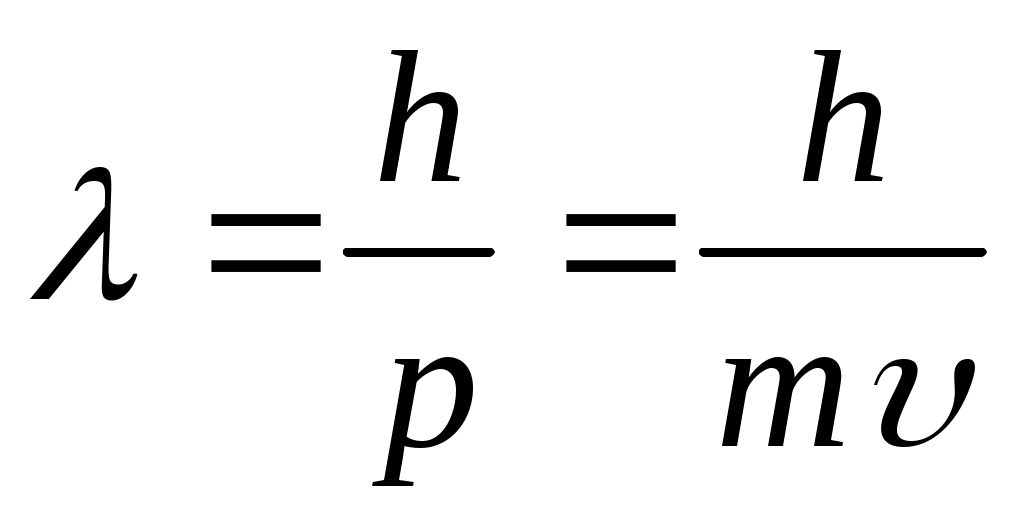 , где h – постоянная Планка ( , где h – постоянная Планка (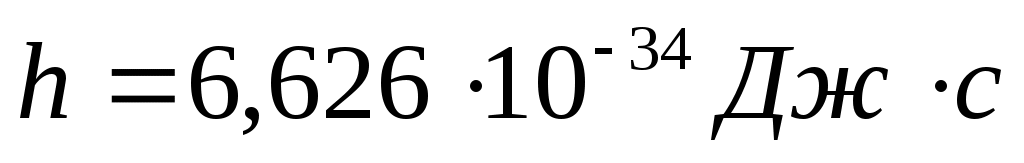 ), m – масса частицы, υ – скорость частицы. Длина волны де Бройля обратно пропорциональна скорости и массе частицы, то есть, если скорости частиц одинаковы, то частица с большей массой имеет меньшую длину волны де Бройля и наоборот. Из представленных частиц большей массой обладает α-частица. ), m – масса частицы, υ – скорость частицы. Длина волны де Бройля обратно пропорциональна скорости и массе частицы, то есть, если скорости частиц одинаковы, то частица с большей массой имеет меньшую длину волны де Бройля и наоборот. Из представленных частиц большей массой обладает α-частица.
Ответ: 3
Ф6.2.1-9
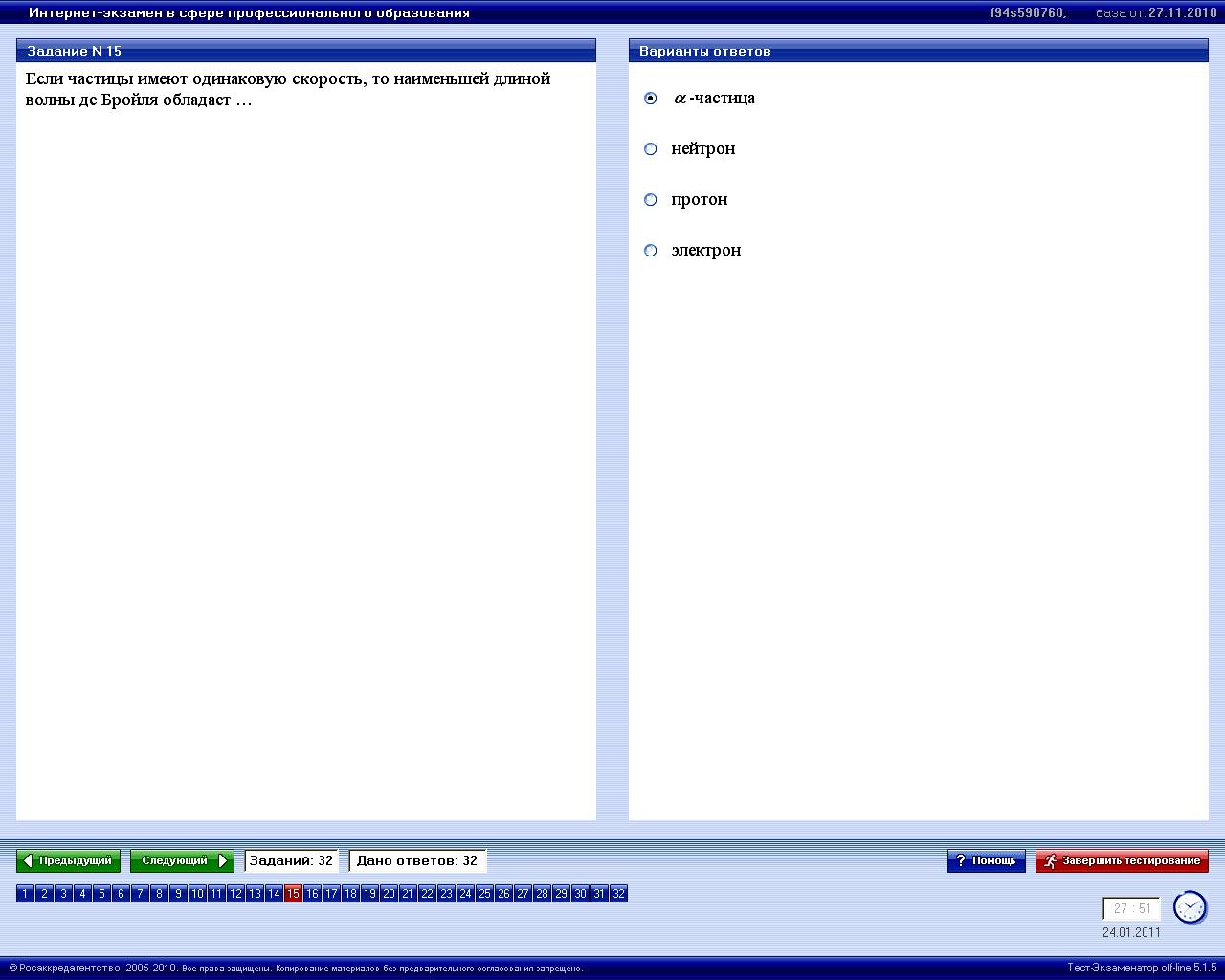
Правильный ответ 1.
Ф6.2.1-10
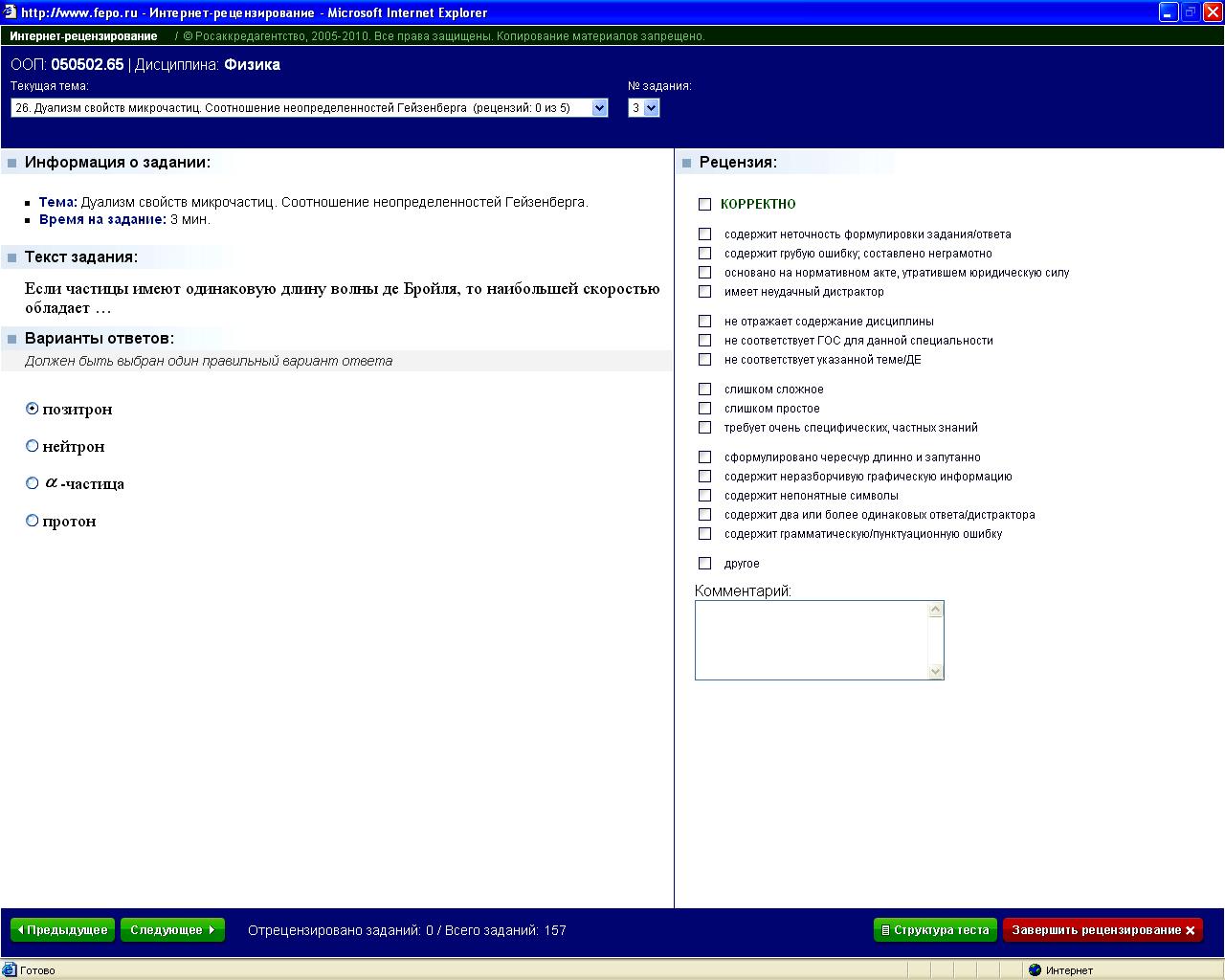
|
1*
|
позитрон
|
2
|
нейтрон
|
3
|
α-частица
|
4
|
протон
|
Ф6.2.1-11
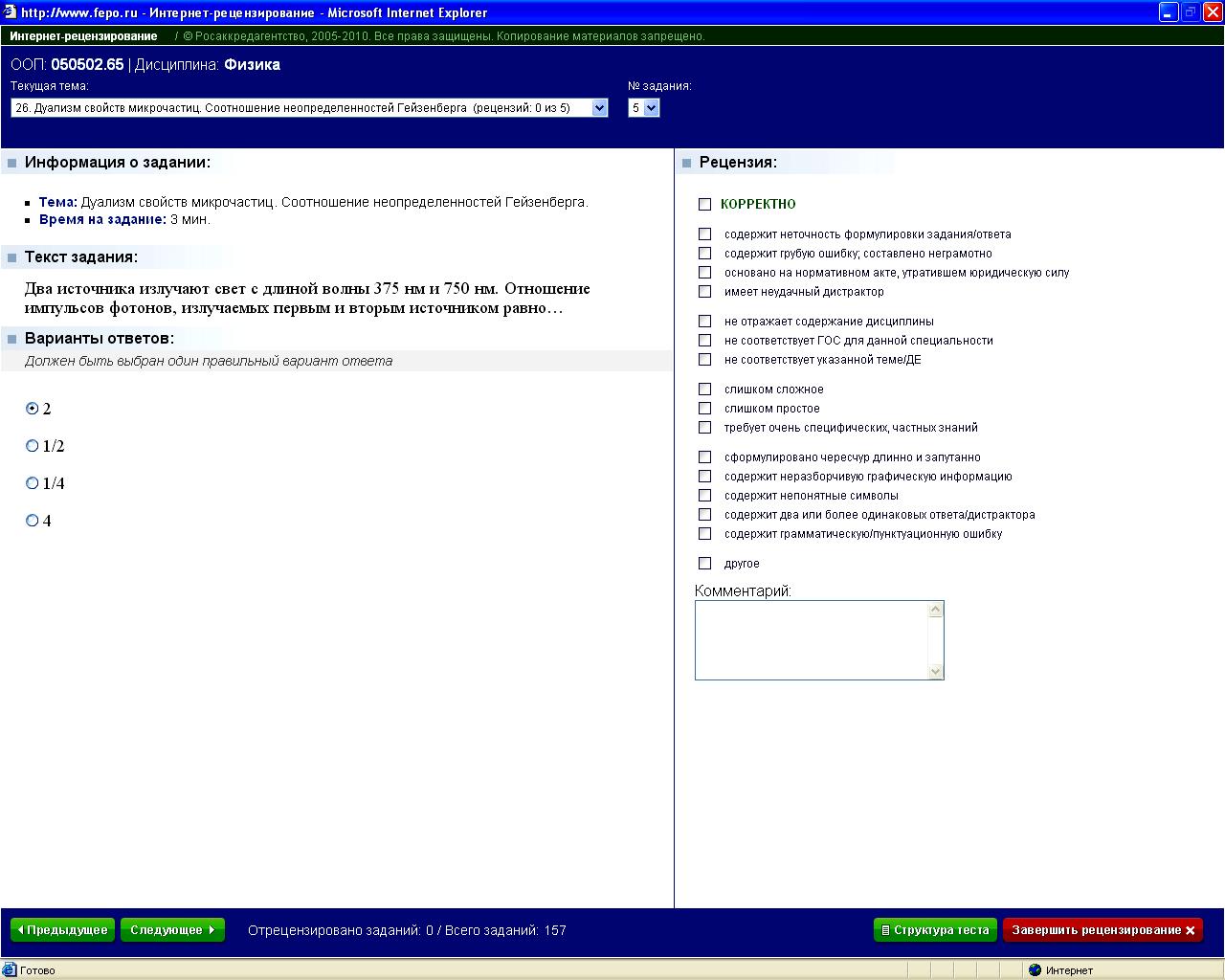
|
1*
|
2
|
2
|
1/2
|
3
|
1/4
|
4
|
4
|
Ф6.2.2-1
Согласно принципу неопределённости и с учётом величины постоянной Планка 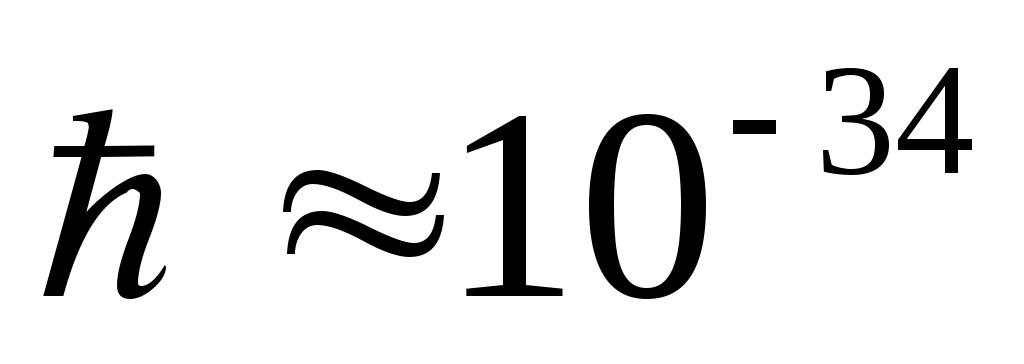 Дж.с, облако свободного электрона массой 9.10-31 кг, первоначально локализованное в области атома с диаметром 10-10 м, за тысячную долю секунды расплывётся до размера порядка … Дж.с, облако свободного электрона массой 9.10-31 кг, первоначально локализованное в области атома с диаметром 10-10 м, за тысячную долю секунды расплывётся до размера порядка …
|
1: 1 м
2: 1 мм
3: 1 км*
4: 1 мкм
|
Принципу неопределенности Гейзенберга удовлетворяет соотношение: 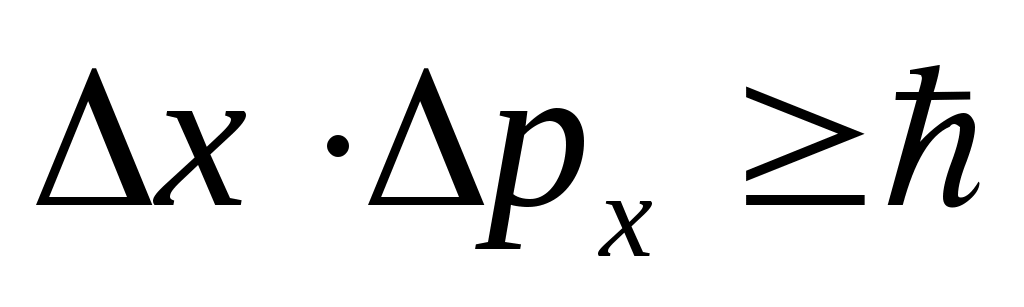 . Преобразуем его: . Преобразуем его:
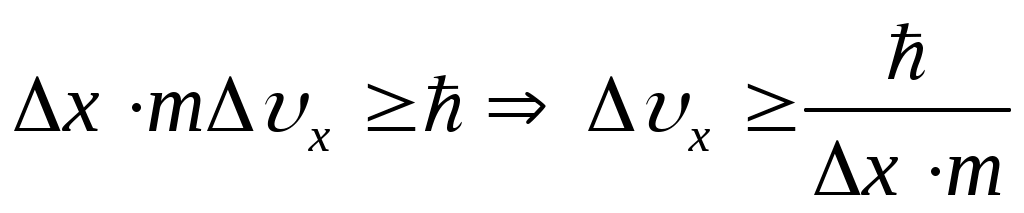 . Определяемый размер . Определяемый размер 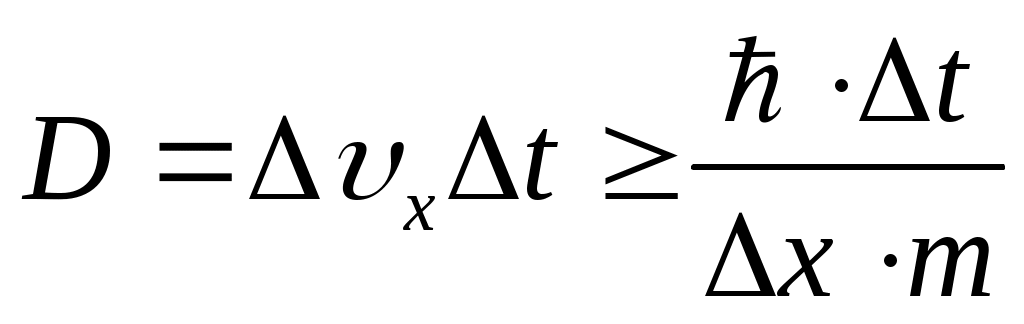 . Подставим исходные данные: . Подставим исходные данные:
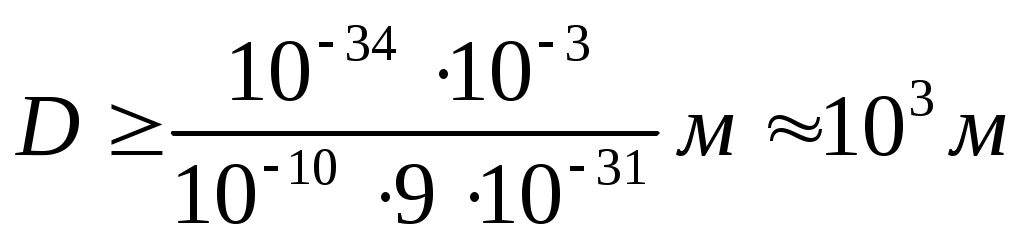 . .
Ответ: 3
Ф6.2.2-2
Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии 10-3 с. Учитывая, что постоянная Планка 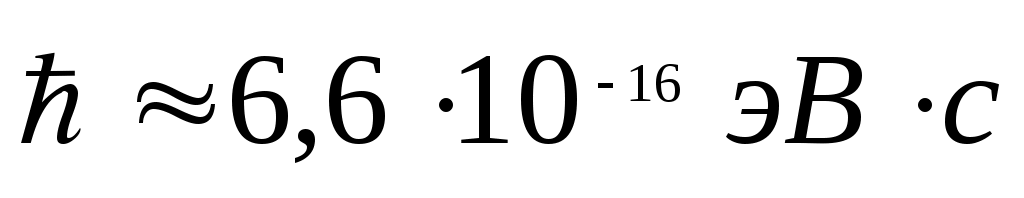 , ширина метастабильного уровня (в эВ) будет не менее … , ширина метастабильного уровня (в эВ) будет не менее …
|
1: 1,5.10-13
2: 6,6.10-13*
3: 1,5.10-19
4: 6,6.10-19
|
Связь ширины уровня и времени жизни определяется формулой (соотношение неопределенности Гейзенберга):
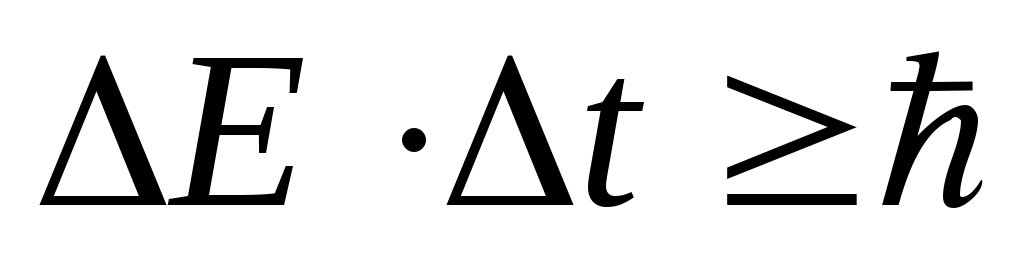 . Отсюда . Отсюда 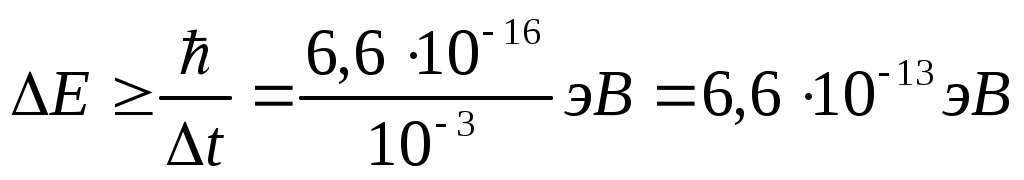 . .
Ответ: 2
Ф6.2.2-3
Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии 10-3 с. Учитывая, что постоянная Планка 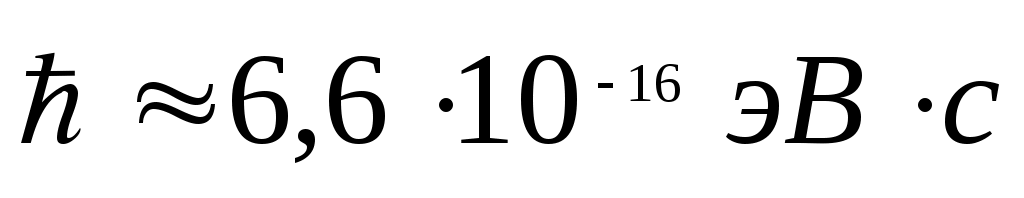 , ширина метастабильного уровня (в эВ) будет не менее … , ширина метастабильного уровня (в эВ) будет не менее …
|
1: 6,6.10-13*
2: 6,6.10-19
3: 1,5.10-19
4: 1,5.10-13
|
Связь ширины уровня и времени жизни определяется формулой (соотношение неопределенности Гейзенберга):
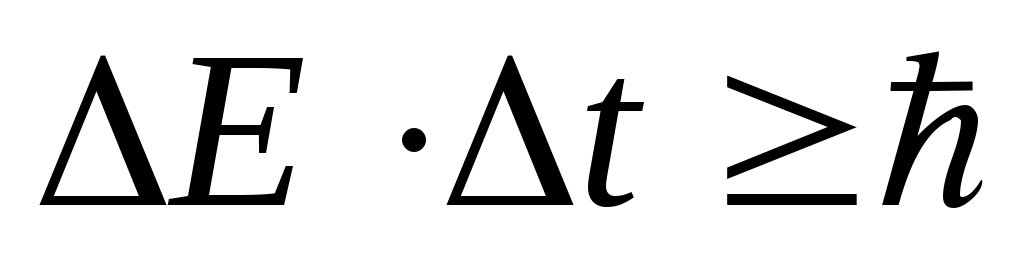 . Отсюда . Отсюда 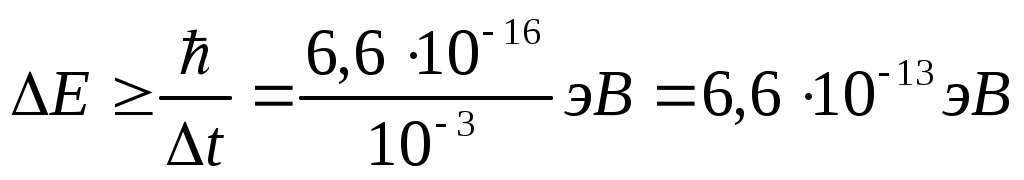 . .
Ответ: 1
Ф6.2.2-4
Положение пылинки массой m=1 мкг определено с неопределенностью 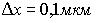 . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка 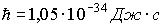 , неопределенность скорости , неопределенность скорости 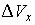 (в м/с) будет не менее… (в м/с) будет не менее…
|
1: 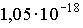 * *
2: 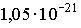
3: 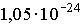
4: 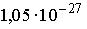
|
Принципу неопределенности Гейзенберга удовлетворяет соотношение: 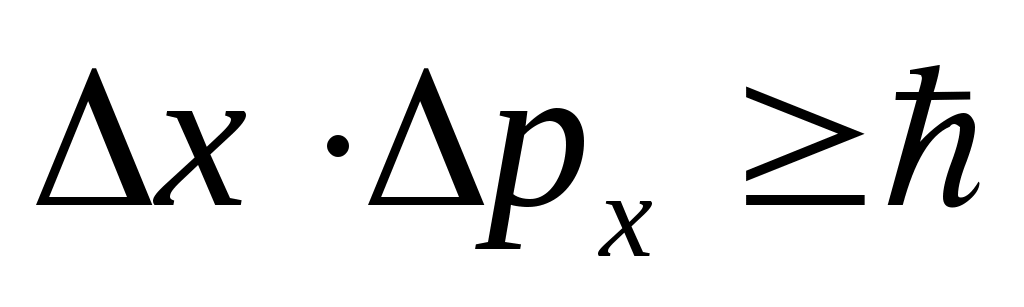 . Преобразуем его: . Преобразуем его:
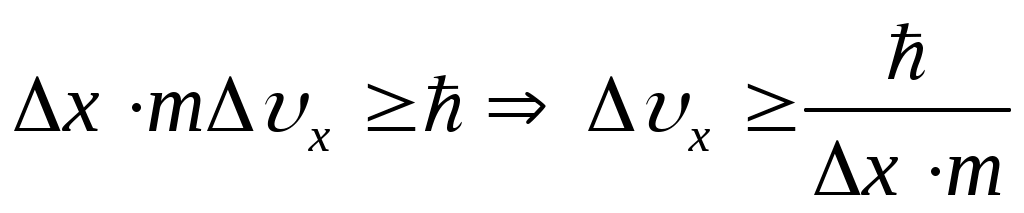 . Подставим исходные данные: . Подставим исходные данные: 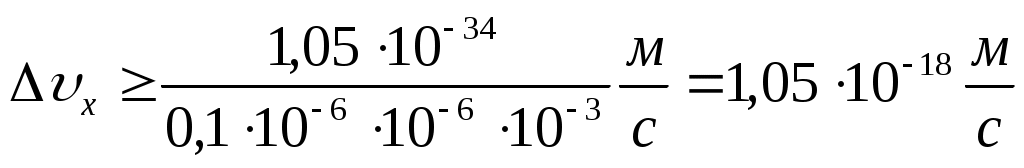 . .
Ответ: 1
Ф6.2.2-5
Электрон локализован в пространстве в пределах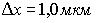 . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка 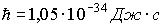 , а масса электрона , а масса электрона 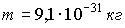 , неопределенность скорости , неопределенность скорости 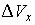 (в м/с) составляет не менее… (в м/с) составляет не менее…
|
1: 115*
2: 0,115
3: 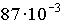
4: 8,7
|
Принципу неопределенности Гейзенберга удовлетворяет соотношение: 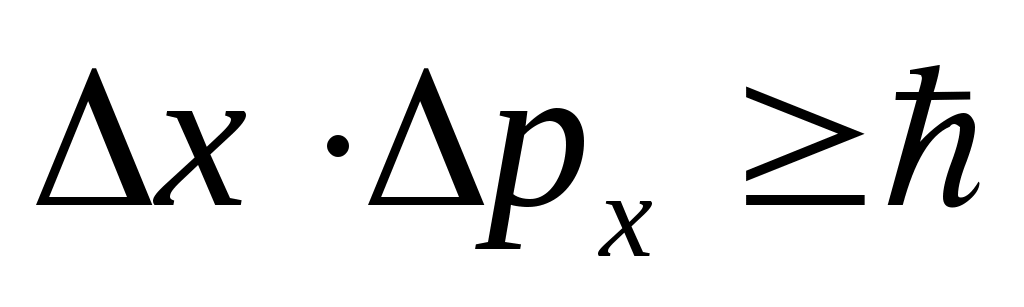 . Преобразуем его: . Преобразуем его:
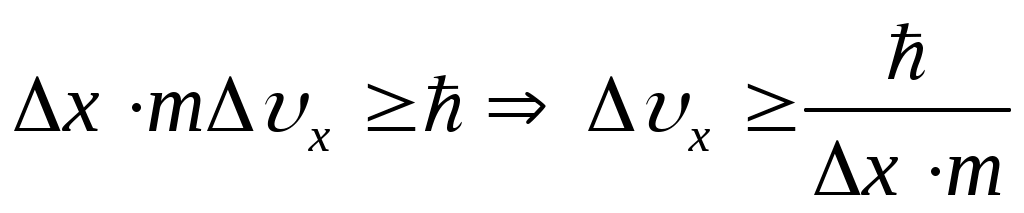 . Подставим исходные данные: . Подставим исходные данные: 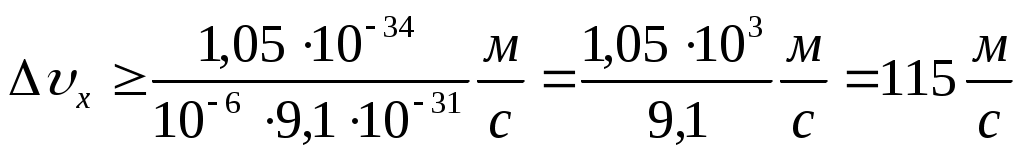 . .
Ответ: 1
Ф6.2.2-6
Протон локализован в пространстве в пределах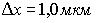 . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка 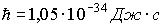 , а масса протона , а масса протона 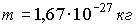 , неопределенность скорости , неопределенность скорости 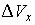 (в м/с) составляет не менее… (в м/с) составляет не менее…
|
1: 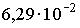 * *
2: 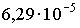
3: 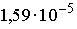
4: 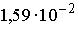
|
Принципу неопределенности Гейзенберга удовлетворяет соотношение: 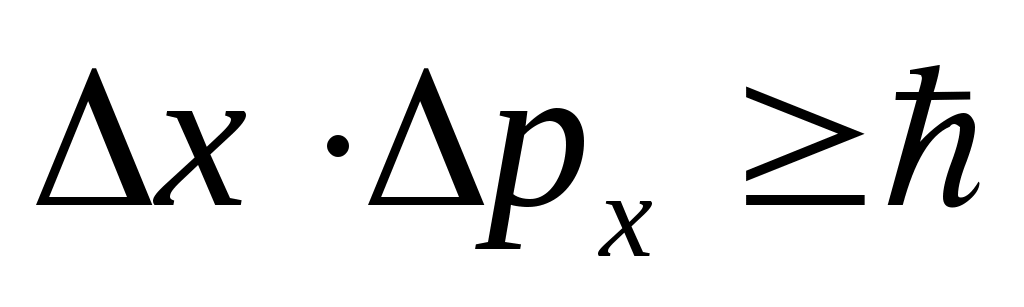 . Преобразуем его: . Преобразуем его:
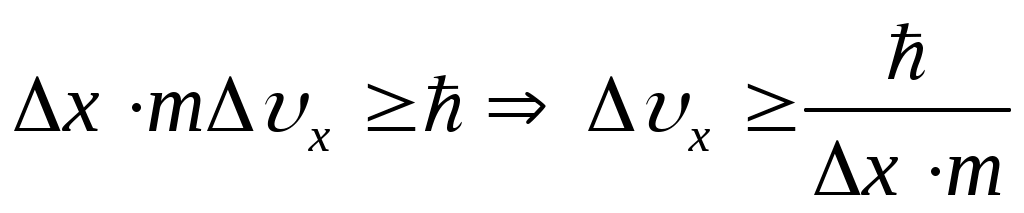 . Подставим исходные данные: . Подставим исходные данные: 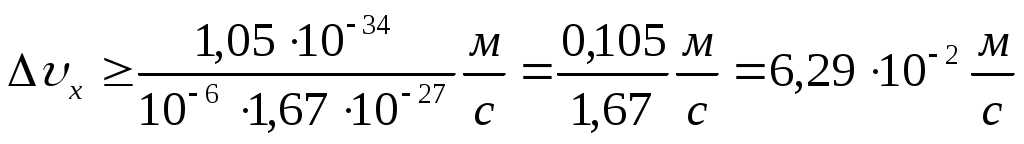 . .
Ответ: 1
Ф6.2.2-7
Время жизни атома в возбужденном состоянии τ = 10 нс. Учитывая, что постоянная Планка 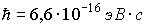 , ширина энергетического уровня (в эВ) составляет не менее… , ширина энергетического уровня (в эВ) составляет не менее…
|
1: 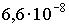 * *
2: 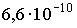
3: 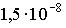
4: 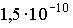
|
Связь ширины энергетического уровня и времени жизни определяется соотношением неопределенности Гейзенберга:
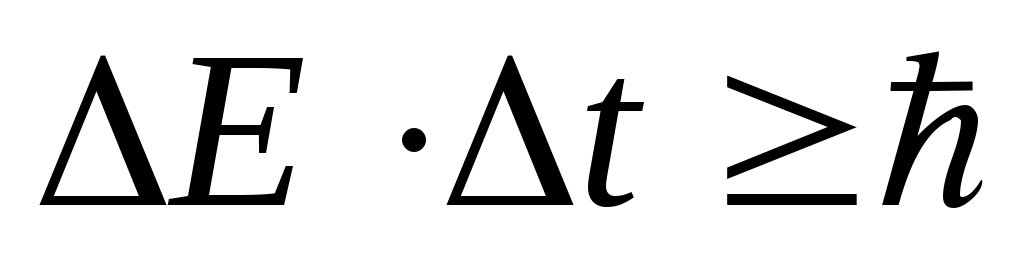 . Отсюда . Отсюда 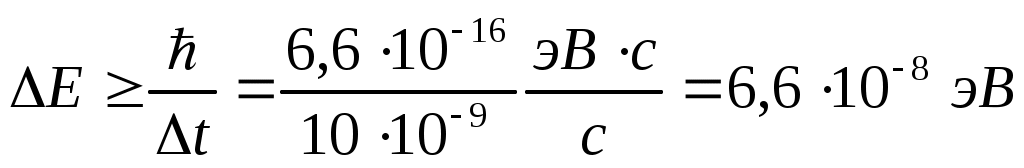 . .
Ответ: 1
Ф6.2.2-8
Положение атома углерода в кристаллической решетке алмаза определено с погрешностью 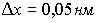 . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка 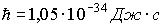 , а масса атома углерода , а масса атома углерода 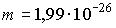 кг, неопределенность скорости кг, неопределенность скорости 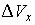 его теплового движения (в м/с) составляет не менее… его теплового движения (в м/с) составляет не менее…
|
1: 106*
2: 1,06
3: 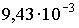
4: 0,943
|
Принципу неопределенности Гейзенберга удовлетворяет соотношение: 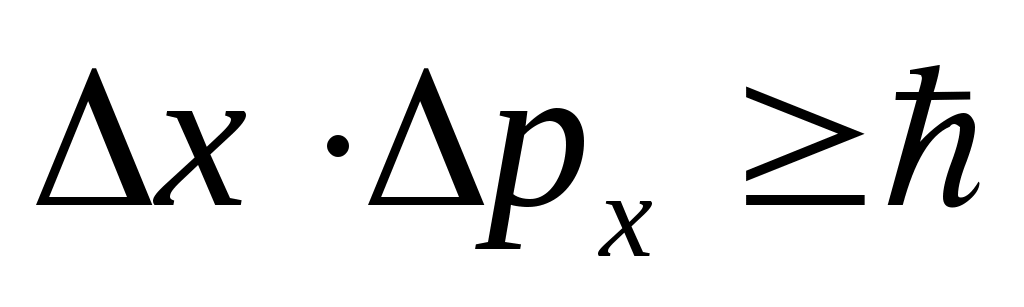 . Преобразуем его: . Преобразуем его:
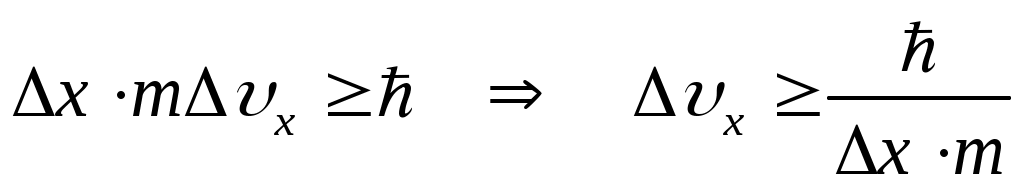 . Подставим исходные данные: . Подставим исходные данные: 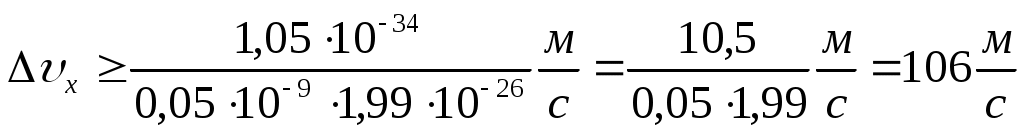 . .
Ответ: 1 |
 Скачать 451.5 Kb.
Скачать 451.5 Kb.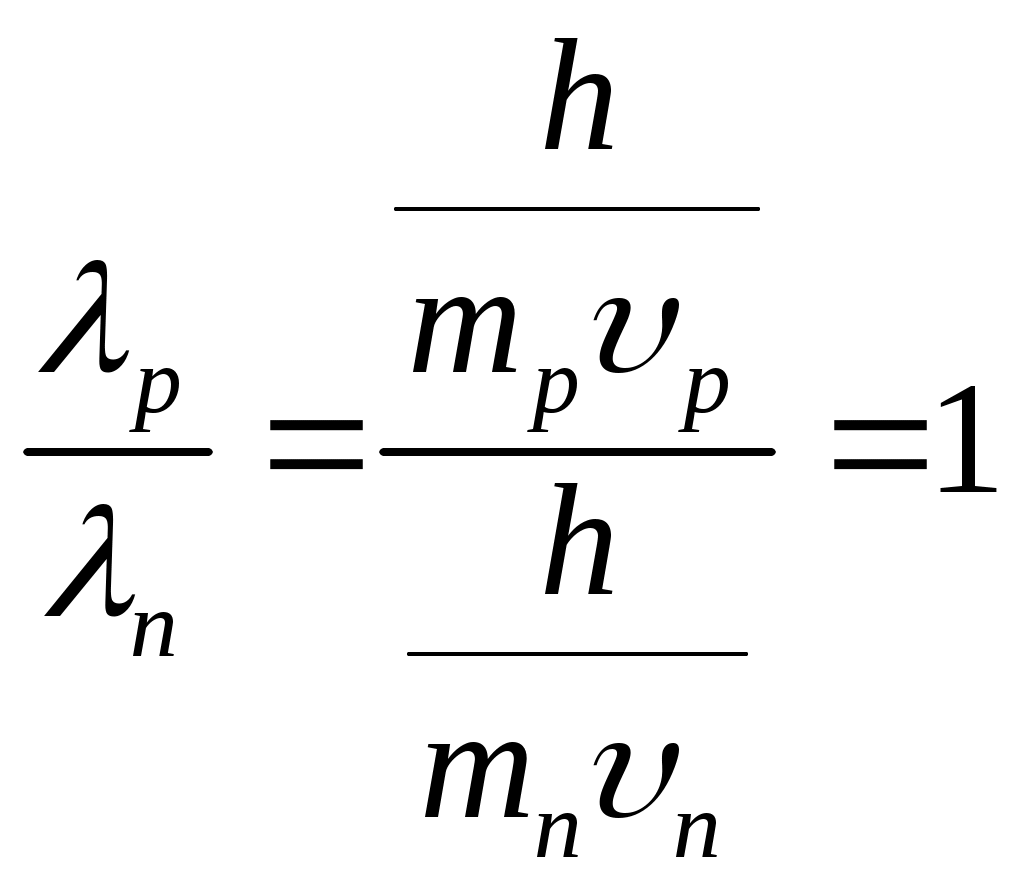 .
.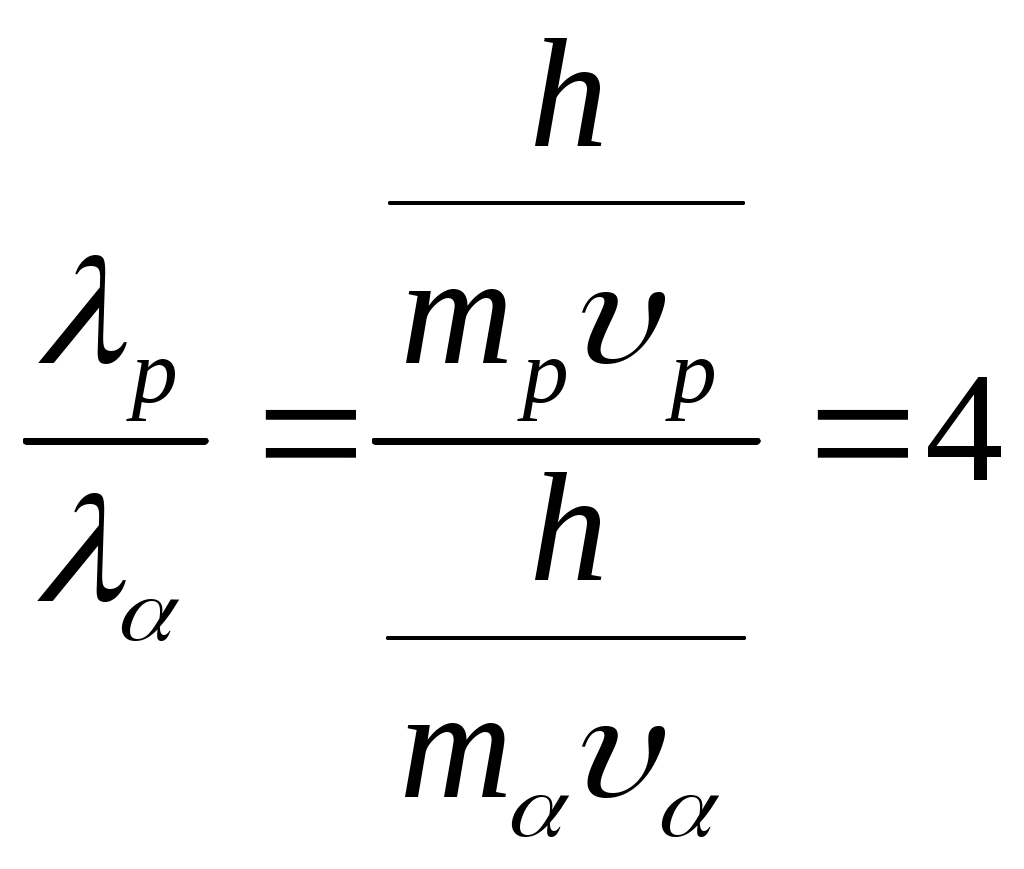 .
.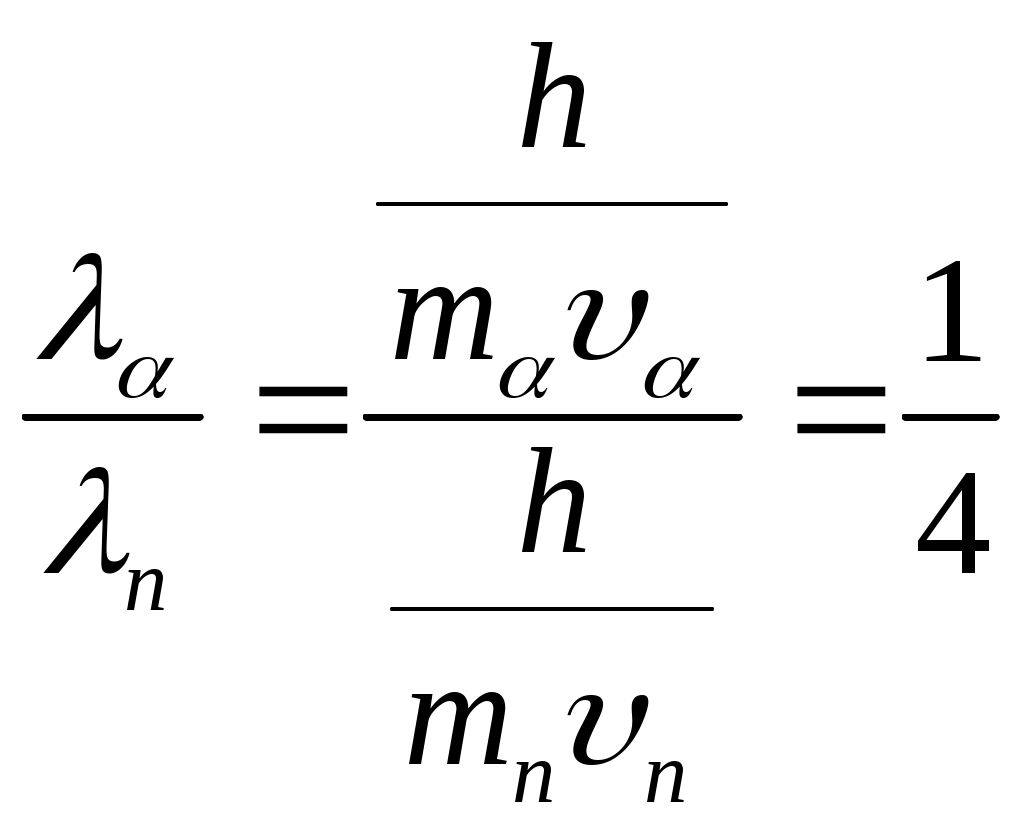 .
.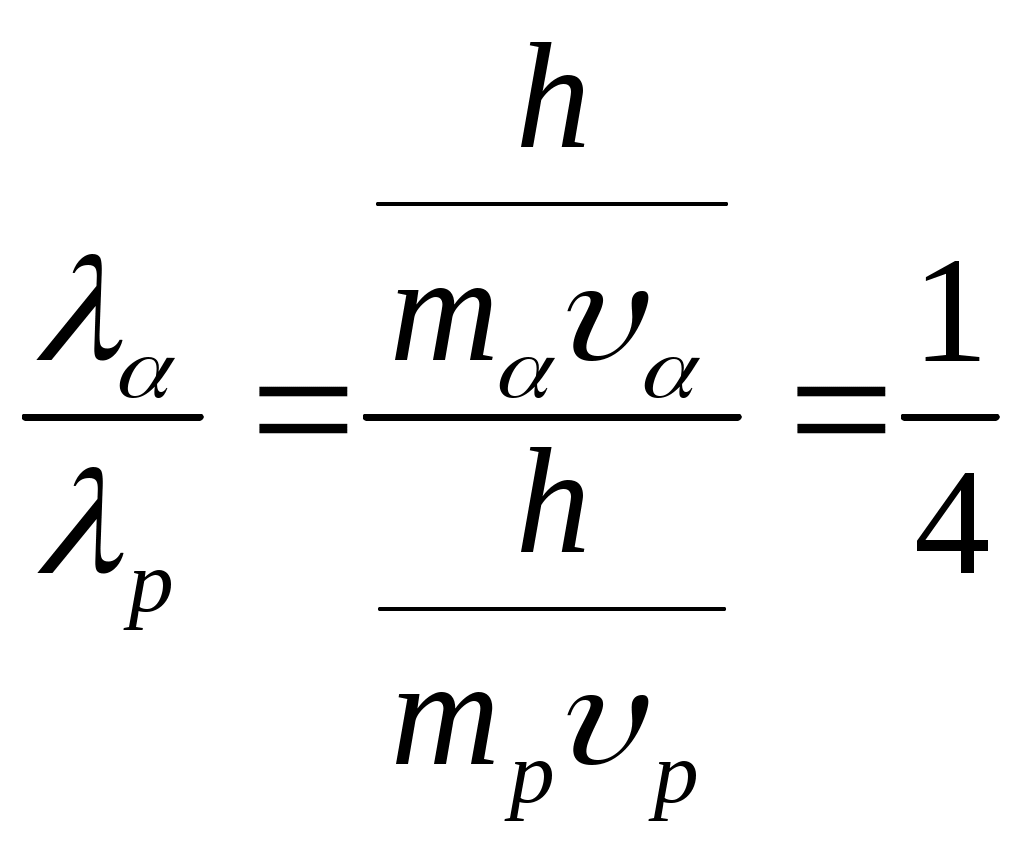 .
.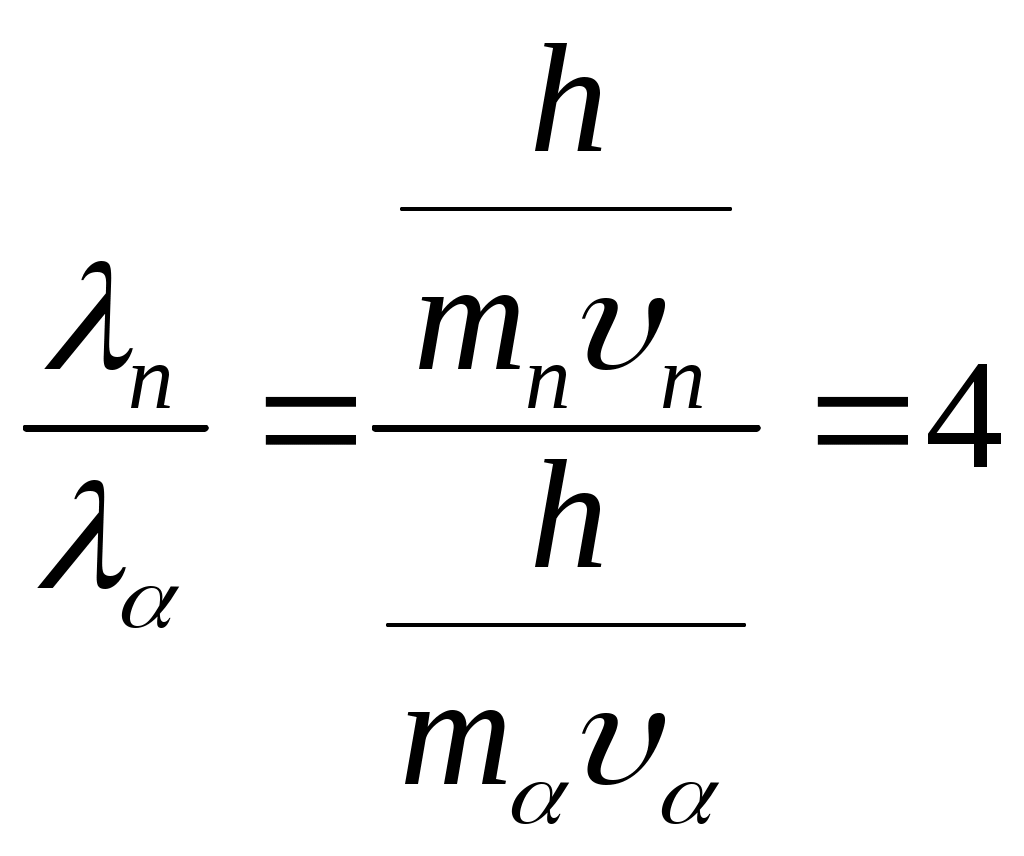 .
.
