Қатты денелердің жылулық қасиеттері.. 10 лекция. 8 Блім. атты денелерді жылулы асиеттері. Кристалдык торды тербелісі. ДюлонгПти заы. Фонон
 Скачать 303.35 Kb. Скачать 303.35 Kb.
|
|
8 Бөлім. Қатты денелердің жылулық қасиеттері. Кристалдык тордың тербелісі. 8.1. Дюлонг-Пти заңы. Фонон. Кристалл белгілі массасы бар қандай да бір ретпен орналасқан атомдар жүйесінен тұрады; атомдар арасында тартылу және тебілу күштері бар, олар атомдардың өзара белгілі тепе-тең арақашықтықтарында бір-бірін теңестіріп тұрады. Атомның тепе-теңдік күйінен ауытқуы кезінде айналмалы күш пайда болады, ол ығысуга қарама-қарсы, шамасы жағынан атомның типіне, оның айналасына жане кристалдағы ығысу бағытына тауелді болады. Тербелістің классикалық теориясы бойынша, мұндай N атомнан туратын «серпімді- байланысқан массалар» жүйесінде өзіндік жиілігі ꙍi, бар қарапайым тербелістер орын алады, мұндагы i-1;2;….; N-4; N-3 жиілігі ωі, болатын тербеліс бір-біріне тәуелсіз болып табылады; атомдардың қозгалысы осы қарапайым тербелістердің суперпозициясы ретінде берілуі мүмкін. Кристалдар мен молекулалардың жылулық қасиеттерінің кванттык жане классикалық теориясында кристалл өзін осы өзіндік жеке жиілігі ꙍi, бар тәуелсіз осцилляторлар жиынтығы секілді көрсетеді. Классикалық теория бойынша Т температурада орта есеппен әрбір осцияллятор кT энергияға ие болады; барлық оспилляторлар 3N-3≈3N, сәйкесінше кристалл U=3NkT энергияға болады. Кристалдың молярлық жылусыйымдылығы C V = (შU/შT )V =NA 3k=3R тең болады. Бұл атақты Дюлонг жане Пти заңы, яғни кез-келген кристалдық заттың молярлық жылусыйымдылығы бірдей жане ол 3R -ге тең. Ол салыстырмалы түрде тек қана жоғары 700-2000 К аралығында жақсы орындалады. Төменгі температураларда ол мүлдем орындалмайды. Кристалдың жылулық қасиеттерінің анағұрлым толығырақ сипаттамасын Эйнштейн мен Дебайдың жасaған кристалдардың жылусыйымдылығының кванттық теориясы береді. Оның негізінде тербеліс энергиясының квантталуы туралы тұжырым, яғни жылулық сэулеленудің кванттық теориясындағы электромагнитік тербеліс энергиясының квантталуы жатыр. Кванттық теория бойынша әрбір қарапайым тербеліс энергиясы жалғыз осциллятор энергиясы сияқты заң негізінде квантталады. ħꙍ энергиясын осциллятордың тербеліс энергиясының квантты (порциясы) ден санайды, ал кванттық өзін фонон деп атайды жне оны өз кезегінде бөлшектің Е=ħꙍ энергиясы жане 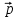 =ħ =ħ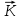 импульстік қасиетіне ие бөлшек ретінде қарастыру қабылданған. Қарапайым тербелістердің өзара тауелсіздігі оларды сипаттау ушін бөлшек-Бозондар ретінде фонондарды қарастыратын Бозе-газ теориясын қолдануға мүмкіндік береді. Келесі тарауларда кристалл тербелісінің кванттық теориясы тэжтрибеде бакыланатын көлтетен зандылыктарды, атап айтканда, жылусыйымдылық рпенен жылуөткізгіштіктің температураға тәуелділігін дұрыс түсіндіруге мүмкіндік беретіні көрсетіледі. Сондай-ақ фонондық деп аталатын бұл теория сәулелердің және зат бөлшектерінің шашырауымен, энергияның жане зарядтың берілуімен байланысты басқа да көптеген құбылыстарды түсіндіруге мүмкіндік береді. Көптеген есептер үшін әртүрлі тәжірибелі әдістер арқылы зерттеуге мүмкіндік беретін фонондардың сипаттамасын білу маңызды. импульстік қасиетіне ие бөлшек ретінде қарастыру қабылданған. Қарапайым тербелістердің өзара тауелсіздігі оларды сипаттау ушін бөлшек-Бозондар ретінде фонондарды қарастыратын Бозе-газ теориясын қолдануға мүмкіндік береді. Келесі тарауларда кристалл тербелісінің кванттық теориясы тэжтрибеде бакыланатын көлтетен зандылыктарды, атап айтканда, жылусыйымдылық рпенен жылуөткізгіштіктің температураға тәуелділігін дұрыс түсіндіруге мүмкіндік беретіні көрсетіледі. Сондай-ақ фонондық деп аталатын бұл теория сәулелердің және зат бөлшектерінің шашырауымен, энергияның жане зарядтың берілуімен байланысты басқа да көптеген құбылыстарды түсіндіруге мүмкіндік береді. Көптеген есептер үшін әртүрлі тәжірибелі әдістер арқылы зерттеуге мүмкіндік беретін фонондардың сипаттамасын білу маңызды.8.2. Фонондарды тәжірибелік зерттеудің әдістері Жеке фононның энергиясы мен импульсін анықтауға мүмкіндік беретін фонондарды зерттеу әдістеріне тоқталайық. Бұл әдістер фононның кристалға түсетін бөлшектермен өзара әсерлесуіне негізделген: нейтрондармен, электрондармен, фонондармен немесе фотондармен (рентгендік, оптикалық немесе инфрақызыл диапазондағы электромагниттік сәулеленумен). Мұндай тәжірибелерде тәуелсіз кристалға түсетін және кристалдан шашыраған бөлшектердің энергиясы жане импульсі өлшенеді, содан кейін энергияның және импульстің сақталу заңы бойынша тәуелсіз фононның энергиясы және импульсі анықталады. Фотонның деформацияланған кристалдық тормен өзара әсерлесуі. Сыну керсеткіші n-ге тең фотон кристалмен Е=ħꙍ энергиямен әсерлессін. Егер кристалда энергиясы Е=ħΩ және импульсі 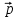 =ħ =ħ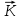 фонон болса, онда фононмен байланысқан серпімді толқын кристалдың бр аймағының сығылуына жэне басқасының созылуына, яғни кристалдың әр түрлі нүктелерінің сыну көрсеткіштерінің n өзгеруіне алып келеді. Түскен фотондар дифрагирленетін дифракциялық тор тордыңдын (35-сурет) баламасы пайда болады. 35-суретте негізгі шашырамаған фотондар шоғынан баска екі дифракциялық минимум пайда болатындығы көрінеді. Фотон қозғалысының бағытының өзгерісі кристалдың тербтербелісн 35-суретте көрсетілген кристалдың сыну көрсеткішінің n модуляциясын туындататын жұтылуға немесе фотонның туындауына негізделген. фонон болса, онда фононмен байланысқан серпімді толқын кристалдың бр аймағының сығылуына жэне басқасының созылуына, яғни кристалдың әр түрлі нүктелерінің сыну көрсеткіштерінің n өзгеруіне алып келеді. Түскен фотондар дифрагирленетін дифракциялық тор тордыңдын (35-сурет) баламасы пайда болады. 35-суретте негізгі шашырамаған фотондар шоғынан баска екі дифракциялық минимум пайда болатындығы көрінеді. Фотон қозғалысының бағытының өзгерісі кристалдың тербтербелісн 35-суретте көрсетілген кристалдың сыну көрсеткішінің n модуляциясын туындататын жұтылуға немесе фотонның туындауына негізделген.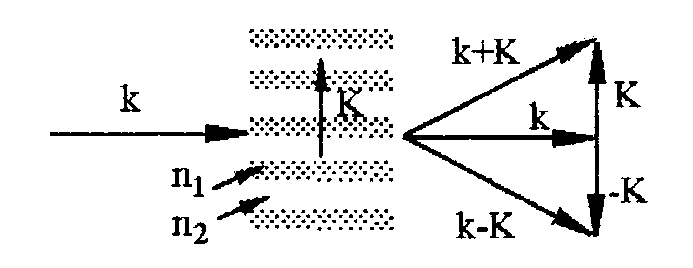 35-сурет. Фотонгың периодты дефармацияланған кристалдық тормен әсерлесу Фотон мен фононның өзара әсерлесуін векторлар кемегімен кескіндеу ыңғайлы (3.2 сурет) Е=hω энергиясы жане 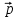 =ħ =ħ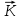 импульсі бар фотон энергиясы Е=ħΩ жане импульсі импульсі бар фотон энергиясы Е=ħΩ жане импульсі 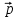 =ħ =ħ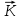 фононның туындауы нәтинәтижесінде және ЕꞋ=ħωꞋ және фононның туындауы нәтинәтижесінде және ЕꞋ=ħωꞋ және 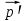 =ħ =ħ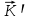 мәндеріне иe болады. Бұл шамалар энергияның және импульстің сақталу заңын сипаттайтын мына қатынаспен байланысқан. мәндеріне иe болады. Бұл шамалар энергияның және импульстің сақталу заңын сипаттайтын мына қатынаспен байланысқан.ħꙍꞋ=ħꙍ+ħΩ және h 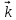 Ꞌ=ħkꞋ+ Ꞌ=ħkꞋ+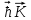 (8.1) (8.1)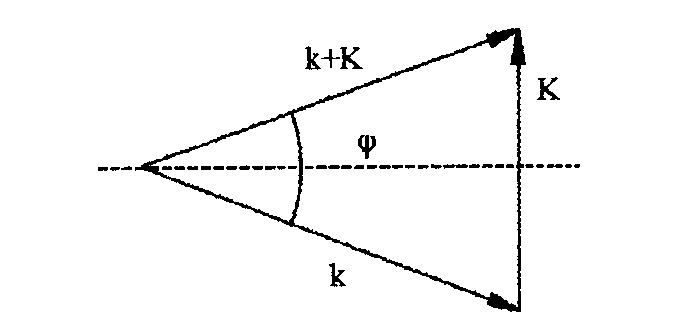 36-сурет. Өзара әсерлескен кездегі фотондар мен фотондардың векторының қатынасы Aйта кететін жағдай, фонондар v мен фотондардың с жылдамдықтарының өте үлкен айырмашылығының әсерінен бірдей мәнге жауап беретін к=К жиліктері мен энергияларының да айырмашылықтары өте үлкен. Шындығында ꙍ=сk; Ω=vK. c>>v болса, онда ꙍ>> Ω. Онда (8.1)-те сәйкес ꙍ≈ꙍꞋ және k≈kꞋ, яғни фононмен әсерлесу кезінде фотонның импульсі мен жиілiгi елеусіз езгереді 36-суретке сәйкес K≈2ksin( 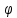 /2) ( 8.2) /2) ( 8.2)Комптон формуласына ұқсас 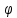 бұрышты жұтылған (туындаған) фононның энергиясы мен фотонның жилігін байланыстыратын формуланы алуга болады. бұрышты жұтылған (туындаған) фононның энергиясы мен фотонның жилігін байланыстыратын формуланы алуга болады.Ω=vK≈(2nꙍꞋ/c)sin( 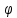 /2) (8.3) /2) (8.3) v/c шамасының аз болуы фотондардың фонондарға шашырауы кезіндегі Ω/ꙍ қатынасының да аз болуына алып келеді. Фотонның сальстырмалы ығысу жиілігі ∆ꙍ/ꙍ де осыған жақын болады және оны тәжірибе жүзінде тіркеу қиын. Фонондардағы жарықтың шашырауы. Фонондардағы жарықтың шашырауын бақылау үшін жоғары монохроматты сәуленің жіңішке ұшқыны пайдаланылады. Белгілі 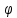 бұрышында шашыраған жарық спектрін тіркейді; осылайша бұрышында шашыраған жарық спектрін тіркейді; осылайша 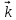 Ꞌ жане Ꞌ жане 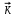 векторларының бағыттары анықталады. Шашыраған сәуле спектрінде жилігі ꙍ бас интенсивті сызықтарына басқа фононның жұтылуы мен туындау процестеріне сәйкес келетін жилігі ±Ω -га ығысқан сызықтар болады. Осылайша тәуелсіз векторларының бағыттары анықталады. Шашыраған сәуле спектрінде жилігі ꙍ бас интенсивті сызықтарына басқа фононның жұтылуы мен туындау процестеріне сәйкес келетін жилігі ±Ω -га ығысқан сызықтар болады. Осылайша тәуелсіз 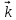 Ꞌ Ꞌ 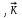 ,ꙍ және ꙍ'-ті, содан кейін ,ꙍ және ꙍ'-ті, содан кейін 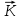 жэне Ω және олардың арасындағы байланысты анықтауға болады. Жарық толқыны үшін жэне Ω және олардың арасындағы байланысты анықтауға болады. Жарық толқыны үшін 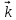 Ꞌ және Ꞌ және 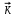 аз болғандықтан, осындай әдіспен аз аз болғандықтан, осындай әдіспен аз 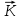 (ұзынтолқынды фонондар) фонондарды зерттеуге болады. (ұзынтолқынды фонондар) фонондарды зерттеуге болады. Фонондардағы рентген сәулелерінің шашырауы. Бұл әдіспен ренттен сәулелері үшін |к| Бриллюн зонасы қатарындай болғандықтан үлкен толқын ұзындықты векторлы фонондарды зерттеуге болады. Тәжірибе сұлбасы жарық шашырауындағы сиякты. Жіңішке монохроматты рентген сәулесінің шоғы пайдаланылады; белгілі бұрышта шашыраған сәуле спектрі тіркеледі; осылайша 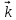 'жане 'жане 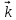 векторларының бағыттары анықталады. Шашыраған сәуле спектрінде жиілігі ꙍ бас интенсивті сызыққа жақын жерде әлсіз сызықтар пайда болады, олар жилігі бойынша бас сызыққа шамалас ±Ω-ға аз ғана ығысқан. Олар фотондардың пайда болу жане туындау процестеріне сәйкес келеді. Сызықтардың жиілік бойынша ығысуы аз болғандықтан, мұндай әдіс бойынша шашыраған фотонның өзгерісін анықтау өте қиын; Ω -нын анықталу дәдәлдігі өте төмен болып табылады. векторларының бағыттары анықталады. Шашыраған сәуле спектрінде жиілігі ꙍ бас интенсивті сызыққа жақын жерде әлсіз сызықтар пайда болады, олар жилігі бойынша бас сызыққа шамалас ±Ω-ға аз ғана ығысқан. Олар фотондардың пайда болу жане туындау процестеріне сәйкес келеді. Сызықтардың жиілік бойынша ығысуы аз болғандықтан, мұндай әдіс бойынша шашыраған фотонның өзгерісін анықтау өте қиын; Ω -нын анықталу дәдәлдігі өте төмен болып табылады. Фонондардағы нейтрондардың шашырауы қазіргі таңдағы фонондарды зерттеудегі ең ақпаратты әдіс болып табылады.Бұл жағдайда толкындық вектордың өзгерісі, сондай ақ нейтрондардың энергиялары да анағұрлым тіркеледі. Нейтрондардың шашырауы кезінде энергияның жан жәнее импульстің сақталу заңын сипаттайтын қатынас дұрыс. 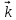 Ꞌ = Ꞌ =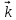 + +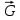 + +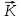 және ( ħkꞋ)2 /2Mn= және ( ħkꞋ)2 /2Mn=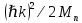 ±ħΩ (8.4) ±ħΩ (8.4)Бұл қатынастағы Мn -нейтрон массасы, 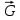 - кері тор векторы. - кері тор векторы.Тәжірибе сұлбасы 37-суретте көрсетілген. Ядролық реактордан Р шығатын жылулық нейтрондар шоғы анағұрлым жаңартылған монокристал монохроматорға М түседі. Одан Вульф-Брэгг заңына сәйкес интенсивті түрде белгілі толқын ұзындықты нейтрондар шашырайды. Осындай жолмен нейтрондар шоғының монохроматталуына жане 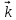 векторының бағытын алуға қол жеткізіледі. Бұл ұшқын зерттеліп отырған үлгі– монокристалға К туседі. Одан шашыраған нейтрондар ұшқыны Вульф-Брегr заңына сәйкес белгілі толқын ұзындықты С есептегішке шағылдыратын монокристал-анализоторга түседі. Анализаторды қолдану векторының бағытын алуға қол жеткізіледі. Бұл ұшқын зерттеліп отырған үлгі– монокристалға К туседі. Одан шашыраған нейтрондар ұшқыны Вульф-Брегr заңына сәйкес белгілі толқын ұзындықты С есептегішке шағылдыратын монокристал-анализоторга түседі. Анализаторды қолдану 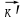 (және олардың энергиялары бойынша) модулді шашыраған нейтрондар спектрін алуға және осылайша шашыраған нейтрондар энергиясын өлшеуге мүмкндік береді. Содан кейін (3.4) қатынасы арқылы тәуелсіз фонон энергиясын Ω, фонон импульсін (және олардың энергиялары бойынша) модулді шашыраған нейтрондар спектрін алуға және осылайша шашыраған нейтрондар энергиясын өлшеуге мүмкндік береді. Содан кейін (3.4) қатынасы арқылы тәуелсіз фонон энергиясын Ω, фонон импульсін 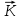 жэне Ω-ның жэне Ω-ның 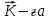 тәуелділігін анықтауға болады, бұл фононның дисперсиялық тәуелділігі деп аталады. тәуелділігін анықтауға болады, бұл фононның дисперсиялық тәуелділігі деп аталады.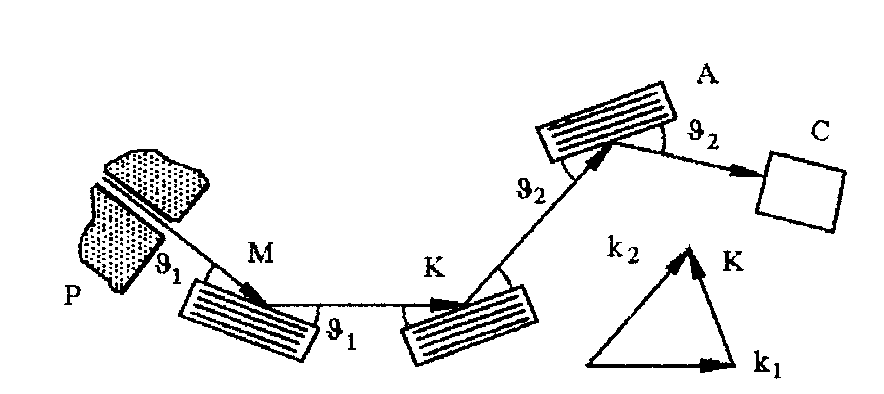 37-сурет. Фононның нейтрондармен өзара әсерлесуі кезіндегі энергиялары мен импулсьтарын тәжірибе жүзінде анықтау Бұл әдіс өте ақпаратты болғанымен уақыттың көп мөлшерін және күшті ядролык реакторларды қолдануды қажет етеді, сондыктан мұндай тәжірибелер қуатты ядролық реакторларға ( жоғары ағынды ) ие бiрнеше iрi ғылыми орталықтарда жүргізіледі. 8.3. Кристалдық тордағы атомдардың тербелісі Фонондардың дисперсиялы тәуелділігі деп аталатын фонон жиiлiгiнiң толқындық векторға тәуелдігін тұрғызудың қарапайым теориялық жағдайын қарастырайық. Жалпы жағдайда бұл мәселе өте қиын және тәртіп бойынша сандык әдістермен есептеледі. Бiратомды ұяшык. Оңай болу үшін кубтык кристалдын бiр атомды базистен тұратын а периодты примитивті карапайым ұяшықты қарастырайық. Бұл кристалда [100] бағытын және осы бағыт бойымен таралатын жазық қума толқынды (көлденең толқын жағдайы да осылайша қарастырылады) қарастырайық (38 – сурет). 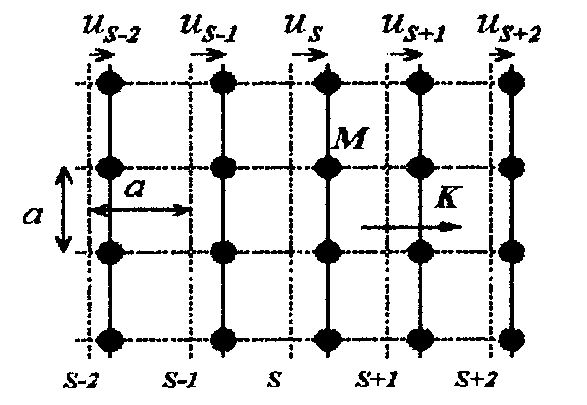 38-сурет.[100] бағыты бойымен таралатын қума жазық, толқындағы біратомдық, кубтық тордың атомдарының тербелісі Бұл жағдайда s номерлi бiр жазықтықта орналаскан ( 100 ) атомдар осы жазыктыққа нормаль бойымен ([100] бойымен ), осы жазыктыққа бiрдей фазамен us шамасына ығысатын болады, яғни атомдардың барлық жазықтығы бір тұтас тербелетін болады. Бұл жазықтықтағы s номерлi таңдап алынған атомға басқа Fsp , күшпен s+р нөмерлi жазықтық әсер ететін болады. Аз ғана us ығысу жағдайында бұл күш олардың тепе теңдiк жағдайында әсерлесуші жажазықтықтардың us+p-us ығысу айырымына пропорционал деп болжауға болады. Қорытынды Fs, күшi Fsp күштердің қосындысы болып табылады: Fs = 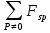 =P =P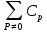 (us+p -us) (8.5) (us+p -us) (8.5)s нөмірлі жазықтықта орналасқан М массалы атом үшін Ньютонның екінші заңын жазамыз: M 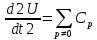 (us+p - us) (8.6) (us+p - us) (8.6)Жазық қума толқын үшін us функциясын табайық 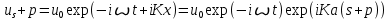 (8.7) (8.7)(3.7) теңдеуін (3.6) теңдеуіне қойып және жалпы көбейтінділерді қысқарта отырып үшін мына теңдеуді аламыз: 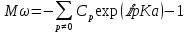 (8.8) (8.8)Қарастырылып отырған тордың симметриясын CP =C-P және cos(a)=(exp(ia)+exp(-ia))/2 қатынасын есепке ала отырып мына теңдеуді аламыз; 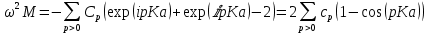 (8.9) (8.9)Көбінесе берілген атомға тек қана жақын орналасқан жазықтықпен байланысын қарастырумен шектеледі.Онда p=±1, және ꙍ2 үшін теңдеу жеңілдетіледі; ꙍ2=(2/M)C1(1-cos(pKa))=(4C1/M)(sin(Ka/2))2 (8.10) ɷ(К) тәуелділік графигі 39 – суретiнде кескінделген. Көрiнiп тұрғандай бiрiншi Бриллюэн зонасының шекарасына сәйкес келетін К = π/ а нүктесінде К бойынша (К) туындысы нөлге тең, бұл фононныңтоптық жылдамдығының нөлге тең екендiгiне сәйкес келедi. 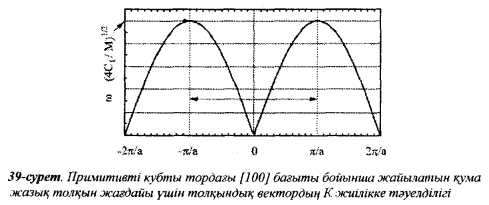 39-сурет. Примитивті кубты тордағы [100] бағыты бойынша жайылатын қума жазық толқын жағдайы үшін толқындық вектордың К-жиілікке тәуелділігі Таңдап алынған атомның бірнеше атомдық жазықтықтармен әсерлесуін ескере отырып, дәл осындай (К) тәуелділігі үшін ерекшелік (8.9) дан да шыгады. (8.7) қатынасына сәйкес К = π/ а жағдайында көршi атомдар қарама – қарсы фазада қозғалады, бұл атом орналасқан жерлерінде ұшқынды тұрғын толқынға сәйкес келеді. Бұл кездегi тұрғын толқынның пайда болуы әрбір атомныңшағылшағылғақынына және шағылған толқынның интерференциялық күшеюімен байланысты. Шын мәнінде, а қашықтықта орналасқан, атомдардан шағылған Толкындардын күшею шарты (39 – сурет) мынадай түрге енеді. ∆ опт =2a=λn=2π/K (n=1), мұндағы К=π/a. Фонондар үш өлшемді торда атомдық жазықтықтан рентген сәулесіне ұксас шағылуға қабілетті; бұл жағдайда интерференциянын күшею шарты Вульф – Брегт теңдеуiнiң түрiне енеді. Бұл фононнын толкындык векторынын Бриллюэн зонасының шекарасына түсу шартына ұқсас. Егер К шамасына керi тордың векторына тек 2πn/ а шамасын қосып немесе алатын болсак (8.7) теңдеуiндегi толқындағы атомдардың тербелісінің сипаттамасында атомдардың қозғалыс заңы бiрдей болып табылады. Сондықтан бiздiң қарапайым жағдайда атомдардын қозғалысын сипаттау үшін К <п /а шартын қанагаттандыратын К мәнiн қолдану жеткілікті. Үшөлшемді жағдайда бұл шартты бiрiншi Бриллюэн зонасынын iшiнде жататын К мәні қанағаттандырады. Ұяшықтағы екі атомдық базистен тұратын атомдардың қозғалысы. Кубтық кристалды қарастыруды оңайлату үшiн екi атомды базистен және а периоды бар примитивті элементар ұяшыкты карастырайык (40 – сурет). Атомдар M 1 және М2 массаға ие болсын. 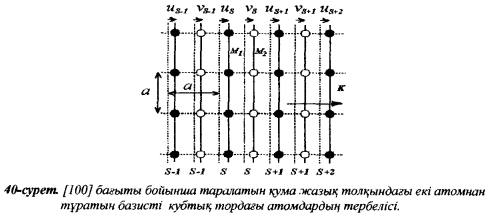 40-сурет. [100] баеыты бойынша таралатын қума жазық, толқындағы екі атомнан туратын базисті кубтық, тордағы атомдардың тербелісі. Бұл кристалда осы бағыт бойымен таралатын [100] бағытын және жазық қума (көлденең толқын жағдайы да осылай қарастырылады) толқынды қарастырайық. Бұл жағдайда 40 суретте қарамен көрсетілген s номерлi (100) бiр жазықтықта орналаскан М1, массалы атом осы жазыктыққаа нормал бойымен бiр фазада us шамасына ығысады, яғни атомдардың бүкіл жазықтығы тұтас ретінде тербелетін болады. Сәйкесінше (40 – сурет) s номерлi бiр жазықтықта орналасқан М2 массалы ашық түстi атомдар осы жазықтыққа [100] нормаль бойымен бірдей фазада Vs шамасына ығысатын болады, яғниатомдардың бүкiл жазықтығы тұтас ретiнде тербелетiн болады. Қосымша өте маңызды жеңілдету ендірейік: s номерлi жазықтықта таңдап алынған бір атомға екi жақын орналаскан жазықтықтағы атомдар ғана әсер етеді деп есептейiк. us және vs аз ығысулар жағдайында жақын орналасқан жазықтықтагы атомдар тарапынан әсер етуші күш us+1 – vs және vs – us , ( ашык түстi атомдар үшін ) және олардың тепе - теңдік жағдайы үшiн жакын орналаскан жазықтықтардың us-vs-1 және vs – us (қара түстi атомдар үшiн) ығысулар айырымына пропорционал. S номерлi жазықтықтағы «қара » және « ашық » атом үшiн Ньютонның екінші заңын (40 сурет) жазамыз. M1 d2 us /dt2=C((vs-1-us)+(vs-us)); M2d2vs/dt2=C((us+1-vs)+(us-vs)); (8.11) us және vs функциясын жазық қума толқын түрінде іздейміз: us=u0exp(-iωt)exp(iKas); vs=v0exp(-iωt)exp(iKas) ( 8.12) (8.12) теңдеуін (8.11)-ге қоя отырып u және v салыстырламы біртекті екі сызықты теңдеулер жүйесін аламыз: -ω2M1u=Cv(1-exp(-iKa))-2Cu -ω2M2u=Cu(1+exp(-iKa))-2Cv (8.13) Егер оның анықтамасын нөлге тең болатын болса, нөлдік теңдеу пайда болады. 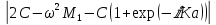 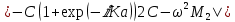 (3.14) теңдеуін мына түрде жазуға болады: 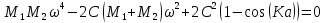 K туындысы кезінде (8.15) теңдеуінің шешімінің 41-суретте келтірілген. 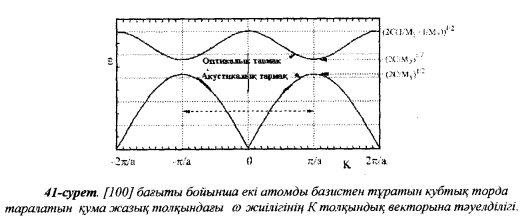 41-сурет. [100] бағыты бойынша екі атомды базистен тұратын кубтық; торда таралатын қума жазық толқындағы а> жиілігінің К толқыноық векторына тәуелділігі. Бұл теңдеудің аса маңызды шешiмi мына жағдайларда болады: 1) К аз мәнінде және 2) K= 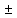 π/ a мәнiнiң айналасында. π/ a мәнiнiң айналасында.Аз K жағдайында cos(Ka) <1- (½) K²a² мәнi мынадай болады. Онда (8.15) Теңдеуi екi түбiрге ие болады: ω ²≈ 2C / (1 / M1+ 1 / M2); ω²≈ CK 2a 2 / 2 (M1 + M2)(8.16) Бiрiншi түбір фононның дисперсиялык тәуелдiлiгiнiң (K) оптикалық тармағына сәйкес келеді, ал екінші түбір фононнын дисперсиялык тәуелдiлiгiнiң (K) акустикалық тармағына сәйкес келеді. Оптикалық тармақ үшін (8.13) теңдеуден, атомдар шамамен қарама – қарсы фазада тербелетiнi шығады, атап айтканда K≈0 кезiнде u/v 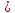 -M1/M2 шарты орындалады. Тербелiстiң мұндай түрін (42б – сурет) электромагниттік толқынның 1 және 2 атомдарының әр түрлi зарядтары жағдайында айнымалы электр өрiсi аркылы қоздыруға болады; осыдан барып «оптикалык фонон» атауы шыққан. Айта кететін жағдай, қарастырып отырған жағдайда магнит өрісінің әсерін ескермеуге болады, себебі электродинамика заңы бойынша қозғалыс жылдамдығының аз мәнi кезiнде толкыннын магнит өрісі зарядтарға әлсіздеу әсер етеді. -M1/M2 шарты орындалады. Тербелiстiң мұндай түрін (42б – сурет) электромагниттік толқынның 1 және 2 атомдарының әр түрлi зарядтары жағдайында айнымалы электр өрiсi аркылы қоздыруға болады; осыдан барып «оптикалык фонон» атауы шыққан. Айта кететін жағдай, қарастырып отырған жағдайда магнит өрісінің әсерін ескермеуге болады, себебі электродинамика заңы бойынша қозғалыс жылдамдығының аз мәнi кезiнде толкыннын магнит өрісі зарядтарға әлсіздеу әсер етеді.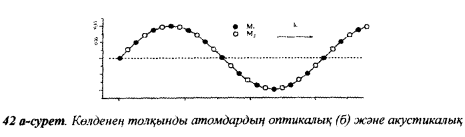 42а-сурет. Көлденең толқынды атомдардың оптикалық, (б) жэне акустикалық;(а)типті жағдайындағы атомдарының ауытқуы 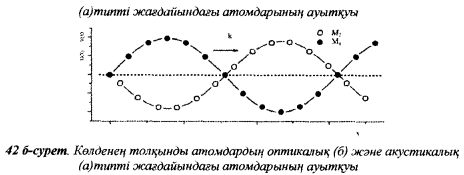 42 б-сурет. Көлденең толқынды атомдардың оптикалық, (б) жэне акустикалық;(а)типті жағдайындағы атомдарының ауытқуы (3.13) теңдеуден акустикалық тармақ үшiн атомдар шамамен бірдей фазада тербеледі, атап айтканда K≈0 кезiнде u / v =1 шарты орындалады. Тербелiстiң мұндай түрiн (42а сурет) кристалға айнымалы серпiмдi әсер арқылы қоздыруға болады. Атомдар келiсiлген түрде шамамен бiрдей фазада қозғалатын болса, онда ол ұзынтолқынды келтiрiлген бiртекті ортада атомдардың акустикалық тербелiсiне сәйкес келедi; осыдан барып «акустикалық фонон» атауы шыккан. Көпатомды тордағы атомдардың тербелiсiн екі атомды сиякты схема бойынша қарастыруға болады. Бiрақ та бұлай қарастыру математикалық көзкарас бойынша өте киын (өте көп теңдеулер санын шешу кажет болады, бiртекті жүйенің (3.14) аныктауышы үлкен қатарға ие болады және сол сияқты). Жоғарыда қарастырганга ұксас r атомнан тұратын ұяшык үшiн көлденең толқын үшін де, қума толқын үшiн де, r түбірлі (3.14) типтес теңдеу пайда болады, олардың бір бөлігін акустикалық тармаққа, ал екінші бөлiгiн ω(К) тәуелділігінің оптикалық тармағына жауап береді деп саналады. Барлығы ω(К) тәуелдiлiгiнiң үш 3r – 3 оптикалык және акустикалык тармақтары пайда болады, ал косындысында 3r фонондык спектрдiң тармағы. Кристалдың iшкi энергиясын (соңынан жылусыйымдылықты) барлық нормал тербелістерiнiң жиiлiгiн аныктау жолымен және Бозе – Эйнштейн таралуын пайдалана отырып барлык осцилляторлардың энергиясы көмегімен анықтауға болады. Егер есептiң екінші бөлiгi қиындық туғызбаса, онда бiрiншi бөлiгi математикалык тұрғыда өте киын, ол қазiргi таңда тек салыстырмалы қарапайым молекулалар үшін ғана шешімін тапқан. Сондықтан осциллятордың өзіндік жиілігінің спектрін анықтаудын оңайлатылған жолдары табылған, олардың кейбіреулерi осы тарауда қарастырылған. Эйнштейн моделі. Эйнштейн моделі бойынша барлык атомдар бір біріне тәуелсiз тербеледi делiнедi және барлық атомдардың тербеліс жиiлiктерi бiрдей. Мұндай жағдайда N атомнан кристалдың ішкі энергиясын есептеу үшін бір ғана осцилляторды қарастыру жеткілікті, ал содан кейін алынган нәтижені 3N осциллятор санына кебейту керек. Әрбiр осциллятор ω жиiлiкке ие болсын. Мұндай осцилляторда сакталатын орташа энергия Бозе– Эйнштейн таралуын колдана отырып есептеледі: <Е>= Мұндағы Ол кезде NA атомнан тұратын кристалл энергиясы былай есептеледi < Emol> = 3NА, CV = (ðЕ/ðT)v= 3NA k (ћω / kT )2exp (ћω / kT ) / ( exp (ћω / kT ) -1)2 ( 8.18 ) Модель 50-100К температурадан (абсолют нолге тым жақын емес) жоғары болғанда тәжiрибемен жақсы сәйкестікте болады. Сv (Т) тәуелділік графигі 43 – суретте көрсетілген. 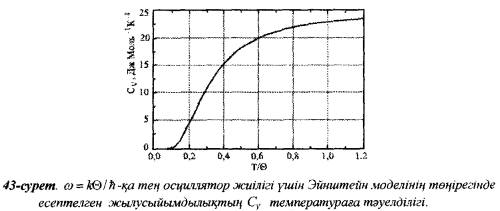 43-сурет. 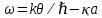 тең осциллятор жиілігі үшін Эйнштейн моделінің төңірегінде есептелген жылусыйымдылықтың Сv температураға тәуелділігі. тең осциллятор жиілігі үшін Эйнштейн моделінің төңірегінде есептелген жылусыйымдылықтың Сv температураға тәуелділігі.Атақты Дюлинг және Пти занына сәйкес 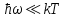 кезiнде (кездейсоқ, жоғары температуралар) кезiнде (кездейсоқ, жоғары температуралар) 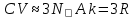 болады. ћω>> КТ кезiнде термодинамиканың үшінші заңы бойынша (кездейсоқтөменгi температураларда)T→0 кезiнде C=3Nk (ћω/kT)² exp (- ћω/kT)→0. Бiрақ та Сv(Т)-ның азаюы (Cv болады. ћω>> КТ кезiнде термодинамиканың үшінші заңы бойынша (кездейсоқтөменгi температураларда)T→0 кезiнде C=3Nk (ћω/kT)² exp (- ћω/kT)→0. Бiрақ та Сv(Т)-ның азаюы (Cv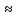 constT3)-ның тәжірибелік бақылағаннан жылдамырақ болады. Бұл жекелеген атомдардың тәуелсiз тербелістерінің қателiктерiмен байланысты. Атомдардың бiр бiрiмен байланыста болатыны белгілі, мысалы, кристалда әр түрлі толқын ұзындықты серпiмдi толқындар болатыны белгілі, ол бiр бiрiне тәуелдi топтық атомдар тербелісіне сәйкес келеді. Эйнштейн моделі бөлме және одан да жоғары температураларда кристалдардың жылусыйымдылығын жақсы сипаттайды. Сондай ақ бұл модель жекелеген молекулалардың жылусыйымдылығын сипаттауға және кристалл жылусыйымдылығының оптикалық фонондарының (әдетте жиiлiгi толкындық векторға әлсіз байланысқан) орнын сипаттауға жақсы сәйкес келеді. constT3)-ның тәжірибелік бақылағаннан жылдамырақ болады. Бұл жекелеген атомдардың тәуелсiз тербелістерінің қателiктерiмен байланысты. Атомдардың бiр бiрiмен байланыста болатыны белгілі, мысалы, кристалда әр түрлі толқын ұзындықты серпiмдi толқындар болатыны белгілі, ол бiр бiрiне тәуелдi топтық атомдар тербелісіне сәйкес келеді. Эйнштейн моделі бөлме және одан да жоғары температураларда кристалдардың жылусыйымдылығын жақсы сипаттайды. Сондай ақ бұл модель жекелеген молекулалардың жылусыйымдылығын сипаттауға және кристалл жылусыйымдылығының оптикалық фонондарының (әдетте жиiлiгi толкындық векторға әлсіз байланысқан) орнын сипаттауға жақсы сәйкес келеді.Атомдардың топтық нормал тербелiсiн есепке алу төменгі температураларда жылусыйымдылыкты сипаттауды нақтылай түседі. Акустикалық топтық тербелістер анағұрлым төменірек жиілікке ие. kТ ретті жылулық тербеліс энергиясы оларды қоздыруға жеткілікті. Мұндай тербелістер төменгі температураларда жылусыймдылыққа өз үлсiн қоса алады. Эйнштейн моделiне сәйкес барлық осцилляторлар бiрдей салыстырмалы үлкен жиiлiкке және көрші энергетикалық денгейлердiң ћω энергияларының айырымына ие, бұның нәтижесінде егер ћω >>kT болса төменгі температура кезiнде осциллятордың бiр деңгейден екіншіге өту мүмкіндігі өте төмен болады, бұл жағдайда ішкі энергия мен жылусыйымдылыққа үлесi де өте аз болады. Кристалдың тербеліс энергиясын есептеп шығару. Жоғарыда айтылып кеткендей нормал тербелiстiң жиiлiгiнiң спектрін есептеу ете қиын мәселе. Сондықтан кристалдағы атомдар тербелісінің энергиясын есептеп шығару үшін әдетте әртүрлі жеңілдетулер колданады. Көп жағдайда фонондардың толқындық векторларының рұқсат етілген мәндері Ферми – газ теориясында жасалған немесе Планк таралуын корытып шығарған схема бойынша атап айтканда, L өлшемді сипаттамаға ие кубтық кристалды қарастырады. Содан кейін кристалдың серпімді тербелiсiн сипаттайтын толқындық функцияларды бірыңғай түрде іздейдi: f(x,y,z,t) = exp (I 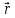 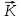 – iωt) (8.19) – iωt) (8.19)Ары қарай кристалдың серпiмдi тербелiсiн сипаттайтын ƒ (x,y,z,t) функциясы түрiнде периодты шеқаралык шарт қойылады : ƒ (x + L, y, z, t) = ƒ (x, y, z, t); ƒ (x, y+L, z, t) = ƒ (x, y, z, t); ( 8.20 ) ƒ (x, y, z + L, t = ƒ (x, y, z, t); Бұл орындалады, егер: exp ( iLKх ) = 1; exp ( iLKy ) = 1 ; exp ( iLK z ) = 1 ; ( 8.21 ) Онда 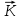 толқындық векторы дискретті мәнге ие болуы мүмкін: толқындық векторы дискретті мәнге ие болуы мүмкін: 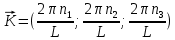 ( 8.22 ) ( 8.22 )мұндағы 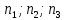 - бутiн сандар. - бутiн сандар. Бұл жағдайда 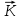 векторының рұқсат етілген бір мәніне К кеңістігіне сәйкес келетін көлем векторының рұқсат етілген бір мәніне К кеңістігіне сәйкес келетін көлем 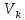 = (2 = (2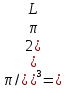 мынаған тең болады, мұңдағы V=L3 кристалдың көлемі. Содан кейiн мынаған тең болады, мұңдағы V=L3 кристалдың көлемі. Содан кейiн 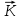 толқындық векторы мен жиiлiктiң белгілі тәуелділігі болжанады. Көбінесе толқындық векторы мен жиiлiктiң белгілі тәуелділігі болжанады. Көбінесе 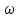 ( (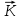 ) тәуелділігі теориялық түрде есептелінеді (3.2 бөлімді қараймыз), ал кейде ) тәуелділігі теориялық түрде есептелінеді (3.2 бөлімді қараймыз), ал кейде 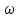 ( (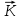 ) тәуелділігінің тәжірибеден алынған мәндері есептелінеді. Бұл тәуелділіктер тәртіп бойынша 3.1 және 3.2 бөлiмде келтірілгендерге ұқсас. Ары қарай ) тәуелділігінің тәжірибеден алынған мәндері есептелінеді. Бұл тәуелділіктер тәртіп бойынша 3.1 және 3.2 бөлiмде келтірілгендерге ұқсас. Ары қарай 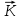 векторының рұқсат етілген мәндерін векторының рұқсат етілген мәндерін 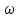 ( (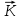 ) елеусіз ғана өзгеретін аралықта аймақтарға бөледі, бұл Эйнштейн моделінде қолданғанға ұксас формулаларды колдану мүмкін болу үшін қажет. Содан кейін, санақ әдістерінің тәртібі бойынша есептелінетін физикалық шаманың барлық аймақтары қосылады, мысалы, iшкi энергияны. ) елеусіз ғана өзгеретін аралықта аймақтарға бөледі, бұл Эйнштейн моделінде қолданғанға ұксас формулаларды колдану мүмкін болу үшін қажет. Содан кейін, санақ әдістерінің тәртібі бойынша есептелінетін физикалық шаманың барлық аймақтары қосылады, мысалы, iшкi энергияны.Сфералық - симметриялы жағдайда ( 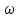 тек тек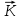 модуліне тәуелді болган кезде) D ( модуліне тәуелді болган кезде) D (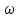 ) жиiлiгi бойынша нормаль тербелістердiң санының таралу функциясын қолданған тиімді, ол оның маңында d ) жиiлiгi бойынша нормаль тербелістердiң санының таралу функциясын қолданған тиімді, ол оның маңында d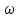 жиiлiгi аралыгында dN нормаль тербелістер санын көрсетеді: жиiлiгi аралыгында dN нормаль тербелістер санын көрсетеді: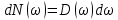 (8.23) (8.23)D ( 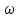 ) ның көмегімен көптеген шамалардын орташа мәнін анықтауға болады, бұл Максвелл таралуларының көмегімен жасалынған схема бойынша, мысалы: ) ның көмегімен көптеген шамалардын орташа мәнін анықтауға болады, бұл Максвелл таралуларының көмегімен жасалынған схема бойынша, мысалы: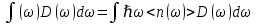 (8.24) (8.24)D ( 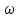 ) функциясы нормал тербелістердің жалпы саны 3N тең болуын талап ететін нормалау шартын қанағаттандыру қажет. ) функциясы нормал тербелістердің жалпы саны 3N тең болуын талап ететін нормалау шартын қанағаттандыру қажет.3N = 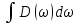 (8.25) (8.25)Осы келтіруді қолдануды Дебай моделiндегi мысалда қарастырайық. Дебай моделі. Дебай моделі төңiрегiнде 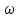 = = 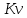 тең деп саналады, мұндағы тең деп саналады, мұндағы 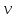 дыбыс толқындарының жылдамдығы. Мұндай келтіру тұтас орта келтiруi деп аталады. Мұндай оптикалық келтiру кезiнде дисперсия мен фонондардың дисперсиялық тәуелділігінің қосымша ν тармағын есепке алу мүмкін емес (3.2 бөлімді қараймыз). Осыган қоса қосымша ν өлшенілген жылдамдық деп саналады, яғни және көлденең және қума толқын жылдамдықтарының арасындағы аралық мәнге ие дыбыс толқындарының жылдамдығы. Мұндай келтіру тұтас орта келтiруi деп аталады. Мұндай оптикалық келтiру кезiнде дисперсия мен фонондардың дисперсиялық тәуелділігінің қосымша ν тармағын есепке алу мүмкін емес (3.2 бөлімді қараймыз). Осыган қоса қосымша ν өлшенілген жылдамдық деп саналады, яғни және көлденең және қума толқын жылдамдықтарының арасындағы аралық мәнге ие 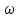 ( (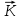 ) тәуелділігі сферикалық симметриялы болып табылады, бұл есептi жеңілдетеді. Берілген жағдайда аз модулді рұқсат етілген. ) тәуелділігі сферикалық симметриялы болып табылады, бұл есептi жеңілдетеді. Берілген жағдайда аз модулді рұқсат етілген. 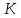 векторларының санын векторларының санын 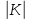 сферасының радиусының көлемін сферасының радиусының көлемін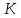 кеңістігіндегі көлемге бөлу арқылы табуға болады: кеңістігіндегі көлемге бөлу арқылы табуға болады: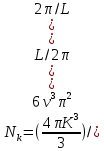 ) (8.26) ) (8.26)D ( 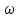 ) функциясын қатынастан табуға болады . ) функциясын қатынастан табуға болады .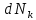 шамасын ұксас жолмен табуға болады, яғни ( 2 шамасын ұксас жолмен табуға болады, яғни ( 2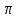 / L)3 шамасын / L)3 шамасын 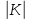 мәнi мәнi 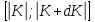 аралығында болатыын аралығында болатыын 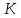 жазықтығындағы қабаттың көлемінің шамасына бөлу арқылы. Онда L3 =V екенін ескере отырып, D ( жазықтығындағы қабаттың көлемінің шамасына бөлу арқылы. Онда L3 =V екенін ескере отырып, D (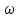 ) үшін мына өрнекті аламыз: ) үшін мына өрнекті аламыз: D( 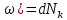 /d /d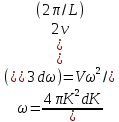 ) (8.27) ) (8.27)Нормирлеу шартын есте сақтау керек. Бұл шарт осцилляторлардың жалпы саны 3N -ге тең болуын қажет етеді. Дебай моделінің төңірегінде K векторының модулін қандай да мүмкін болатын 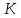 , минималды мәнімен шектейді, бұны (8.26) теңдеуiне қоя отырып, сол бөлігінде берілген типтегі поляризациясының N жалпы санын аламыз (8.26) дан KD және , минималды мәнімен шектейді, бұны (8.26) теңдеуiне қоя отырып, сол бөлігінде берілген типтегі поляризациясының N жалпы санын аламыз (8.26) дан KD және 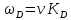 шығара отырып мынаны аламыз. шығара отырып мынаны аламыз. 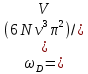 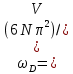 ( 8.28 ) ( 8.28 )D ( 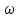 ) функциясының сұлбасы 44 - суретте келтірілген (1 қисық) ) функциясының сұлбасы 44 - суретте келтірілген (1 қисық) 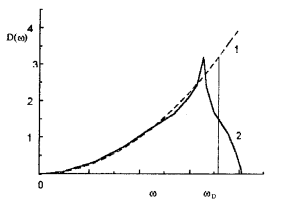 44-сурет.Дебай моделіндегі D ( 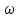 ) күй тығыздығының функциясы ) күй тығыздығының функциясыKD мәнi бiрiншi Бриллюэн зонасына сәйкес келетiн 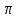 / / мәнiне жақын келедi. Бiрақ та есте сақтайтын жағдай дебай моделінің төңірегінде бiрiншi Бриллюэн зонасына сәйкес келетін мәнiне жақын келедi. Бiрақ та есте сақтайтын жағдай дебай моделінің төңірегінде бiрiншi Бриллюэн зонасына сәйкес келетін  векторынын мүмкiн болатын аймағынын нақты мәнi оған сәйкес келмейтін сферамен алмастырылады. векторынын мүмкiн болатын аймағынын нақты мәнi оған сәйкес келмейтін сферамен алмастырылады.Дебай теориясынын төңiрегiнде осциллятор поляризациясының үш типіне де жауап беретін ішкі энергия интеграл былай шығарылады:  (8.29) (8.29)Мұндағы  және және 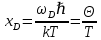 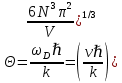 (8.30) (8.30)(8.29) интегралын тек қана сандық әдіс арқылы есептеуге болатынын есте сақтау қажет. 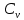 жылусыйымдылығын есептеу үшін (8.29) теңдеуін Т темперетура бойынша дифференциялдау қажет. жылусыйымдылығын есептеу үшін (8.29) теңдеуін Т темперетура бойынша дифференциялдау қажет.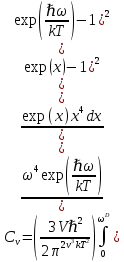 (8.31) (8.31)(8.29) теңдігі түрінде алынған интегралды тек қана сандық әдістер арқылы есептеп шығаруға болады,  тәуелділігі 45-суретте көрсетілген. тәуелділігі 45-суретте көрсетілген. 45-сурет.Дебай моделінің төңірегінде есептелген  жылусыйымдылықтың тәуелділігі. Абцисса бойына Т / жылусыйымдылықтың тәуелділігі. Абцисса бойына Т /  келтiрiлген температура орналастырылған . Температураның жоғары мәнiнде келтiрiлген температура орналастырылған . Температураның жоғары мәнiнде 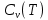 мәнi 3R - классикалық мәнiне ұмтылады (3.4 есебін қараңыз ). мәнi 3R - классикалық мәнiне ұмтылады (3.4 есебін қараңыз ).Температураның аз мәнінде 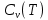 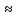 const * T3,осыны көрсетейік. (8,31) тендеуiнде T const * T3,осыны көрсетейік. (8,31) тендеуiнде T 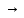 0 кезiнде X 0 кезiнде X  және хD және хD  екенiн еске сақтайық. Онда (8.31) теңдеуінің интегралдау шегі нөл және шексiздiк деп есептеуге болады. Соңғы (8.31) формуладағы интегралдың өзi қандай да тұрақтыға тең болады және (8.31) ден екенiн еске сақтайық. Онда (8.31) теңдеуінің интегралдау шегі нөл және шексiздiк деп есептеуге болады. Соңғы (8.31) формуладағы интегралдың өзi қандай да тұрақтыға тең болады және (8.31) ден   const * T3 тәуелділігі анық көрінеді. const * T3 тәуелділігі анық көрінеді. T → 0 кезiндегi 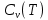 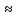 const * T3 занын келесі анық ойлардан алуға болады. Т → 0 кезінде const * T3 занын келесі анық ойлардан алуға болады. Т → 0 кезінде 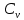 - ға негiзгi үлесті аз жиілікті акустикалық тербелістер (дәл осыларды Дебай моделі сипаттайды) қамтамасыз етедi, яғни kT>ℏ - ға негiзгi үлесті аз жиілікті акустикалық тербелістер (дәл осыларды Дебай моделі сипаттайды) қамтамасыз етедi, яғни kT>ℏ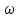 = νℏK. K -кеңістігінде мұндай векторлардың облысы көлемi (kT)3 пропорционал сфера болып табылады. Әрбір фонон орта есеппен (kТ)1 ретті энергияға ие болады. Онда энергия қоры нормал тербелістер санына яғни (kT)4 –ға пропорционал. = νℏK. K -кеңістігінде мұндай векторлардың облысы көлемi (kT)3 пропорционал сфера болып табылады. Әрбір фонон орта есеппен (kТ)1 ретті энергияға ие болады. Онда энергия қоры нормал тербелістер санына яғни (kT)4 –ға пропорционал. 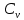 олардың әрбірінің орташа энергиясына жылусыйымдылығын энергияның температура бойынша туындысы ретінде табуға болады: олардың әрбірінің орташа энергиясына жылусыйымдылығын энергияның температура бойынша туындысы ретінде табуға болады: 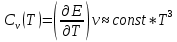 (8.32 ) (8.32 )Осылайша Дебай моделі салыстырмалы түрде төменгі температура кезінде де 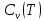 теуелділігін жақсы сипаттайды. Сондықтан оны көбінесе акустикалық тармақтың фонондарының дисперсиялық тәуелдiлiктерiн әсiресе өте төмен температураларда салыстырмалы жылусыйымдылыққа үлестерiн есептеуге қолданады. Сонымен коса, оны нейтрондар мен фотондардың фонондармен өзара әсерлесуін, сәуленің заттан шашырауын болжау үшін қолданады. Әрбір зат үшін олардың жылусыйымдылықтары туралы тәжiрибелiк мәндер арқылы өзінің жеке Дебай температурасы тандап алынған, олар әр түрлі анықтамалықтарда келтірілген. теуелділігін жақсы сипаттайды. Сондықтан оны көбінесе акустикалық тармақтың фонондарының дисперсиялық тәуелдiлiктерiн әсiресе өте төмен температураларда салыстырмалы жылусыйымдылыққа үлестерiн есептеуге қолданады. Сонымен коса, оны нейтрондар мен фотондардың фонондармен өзара әсерлесуін, сәуленің заттан шашырауын болжау үшін қолданады. Әрбір зат үшін олардың жылусыйымдылықтары туралы тәжiрибелiк мәндер арқылы өзінің жеке Дебай температурасы тандап алынған, олар әр түрлі анықтамалықтарда келтірілген. Оптикалық тармақтың фонондарының дисперсиялық тәуелділіктерінің келтірілген аппроксимациясы үшiн көбінесе Эйнштейн моделіне немесе Дебай моделiне ұқсас моделдер құралы, тек ондағы 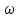 ( (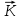 ) тәуелдiлiгiн және математикалық есептеулерін өзгертеміз. ) тәуелдiлiгiн және математикалық есептеулерін өзгертеміз. |
