физика. Дана (1). 8 Жарыты шашырауы. Релей заы
 Скачать 376.23 Kb.
|
|
8.1. Жарықтың шашырауы. Релей заңы Көптеген тәжірибелік деректер бойынша жарық оптикалық біртекті ортада түзу сызықты таралады. Гюйгенстің, Ферманың және т.б.. принциптерінен де дәл осындай қорытынды жасалады. Егер ортада оптикалық біртекті еместіктер пайда болса, онда бұлар жарықтың шашырауын туғызады. Оптикалық біртекті еместіктер әртүрлі себептерден пайда болуы мүмкін. Мысалы, газдағы бөгде заттың қатты бөлшектері (түтін), ауадағы сұйықтың (судың) тамшылары (тұман), сұйықтағы бөгде қатты заттың бөлшектері (суспензия) және т.б. орталарды оптикалық біртекті емес етеді. Осындай оптикалық біртекті емес орталарды бұлдыр (лай) орталар (мутные среды) деп атау қабылданған. Тәжірибеге қарағанда жарық бөгде қоспалары жоқ мөлдір біртекті (таза) орталар арқылы таралған жағдайда да шашырайды екен. Осындай шашырау – біртекті (таза) орталардағы шашырау – жарықтың молекулалық шашырауы деп аталады. Жарықтың шашырау құбылысына бұдан кейінгі зерттеулер нәтижесінде пайда болу механизмі бойынша және барлық басқа белгілері бойынша жарықтың бұлдыр орталардағы және жарықтың молекулалық шашырауынан өзгеше шашыраудың болатындығы анықталды. Бұл – жарықтың комбинациялық шашырауы. 7.3.1 Шашырау процестерінің табиғаты Шашырау табиғаты. Ортаның құрамына ортаны құрайтын негізгі заттың молекулалары немесе атомдары және бөгде бөлшектер (тозаңдар, су тамшылары және т.б.) кіреді. Молекулалардың мөлшері  болса, ал бұдан молекулалардың бірігуінен құралған бөгде бөлшектер – мыңдаған және он мыңдаған есе үлкен болады.Жарықтың шашырау процесінде молекула немесе бөлшек ортада таралатын электромагниттік толқыннан энергия қабылдап алып, осы энергияны төбесі молекулада немесе бөлшекте болатын денелік бұрышқа шығарады. Осы мағынада жарықты молекуланың немесе орасан көп молекулалардан тұратын бөлшектің шашыратуы бірдей іске асырылады, тек бұлардың сәулені қайта шығару механизмдерінде айырмашылық болады. Егер орта үздіксіз деп қарастырылатын болса, онда ортаның оптикалық біртекті еместіктері шашырату көзі ролін атқарады. Осы жағдайда ортаның сыну көрсеткіші бір нүктеден екінші нүктеге көшкенде өзгеріп отырады, ал шашырау болатын аймақтардың «мөлшерлерің сыну көрсеткішінің әдеуір өзгерісі іске асатын қашықтықтармен анықталады. Өзінің физикалық мазмұны бойынша шашырау ортаның біртекті еместіктерінде толқынның дифракциялануы болып табылады. Шашыраудың түрлері. Шашырау сипаты ең алдымен толқын ұзындығы мен бөлшектер мөлшерінің ара қатысына тәуелді болады. Егер бөлшектің сызықтық мөлшерлері толқын ұзындығына қарағанда шамамен  кіші болса, онда шашырау осы шашырау түрін зерттеген Д.У. Рэлейдің (1842-1919) құрметіне рэлейше шашырау деп аталады.Бөлшектердің мөлшерлері үлкен болғандағы шашырауды Ми шашырауы деп атайды. Ми алғаш (1908) дамытқан теория сфералық бөлшектерге ғана қатысты болғанымен «Ми шашырауың термині пішіні дұрыс емес бөлшектер үшін де қолданылады. Кіші бөлшектер үшін Ми теориясы Рэлей теориясының нәтижелеріне алып келеді. Оптикалық біртекті еместіктің маңызды дербес жағдайы дыбыс толқыны таралатын ортаның оптикалық қасиеттерінің біртекті еместігі болып табылады. Осының нәтижесінде кеңістікте ортаның оптикалық біртекті еместігінің гармоникалық үлестірілуі және оптикалық қасиеттердің уақыт бойынша гармоникалық өзгерісі пайда болады. Оптикалық қасиеттердің кеңістіктік гармоникалық біртекті еместігі нәтижесінде дыбыс толқынында жарықтың дифракциясы байқалады. Оптикалық қасиеттердің уақыт бойынша гармоникалық өзгерісі нәтижесінде ортаның әрбір нүктесінде дифракцияланған жарық жиілігінің өзгерісі байқалады. Дыбыс толқынында дифракцияланған жарықтың жиілігінің осы өзгерісі Мандельштам-Бриллюэн құбылысы деп аталады. Бұл құбылысты бір-бірінен тәуелсіз Л.И. Мандельштам (1879-1944) және Л. Бриллюэн (1889-1969) ашқан. Молекулалардың кванттық қасиеттері, шашыраған жарық жиілігінің түсетін жарық жиілігіне салыстырғанда өзгеруімен сипатталатын, жарықтың комбинациялық шашырауында білінеді. Осы шашыраудың ерекше кванттық табиғатына байланысты ол жеке топқа жатқызылады. Көп қайтара шашырау. Бөлшек шашыратқан сәулені өз кезегінде басқа бөлшектің шашыратуы мүмкін және т.т. Осы жағдайда шашырауды көп қайтара шашырау дейді. Бұл әрбір кезекті шашыратуда бір рет шашырату заңдарына сәйкес іске асырылады. Ақырғы нәтиже бір мәрте шашыратулардың нәтижелерін бұлардың бірінен кейін екіншісінің ілесуі статистикалық сипаттамаларын ескеріп қосындылаумен алынады. 7.3.3 Рэлейше шашырау Оптикалық біртекті ортада жазық толқынның шебі өзіне-өзі параллель орын ауыстырады. Бірақта егер орта біртекті болмай және мұнда оптикалық қасиеттері басқаша қоспалар болса, онда бастапқы бағытта таралатын толқыннан басқа, жан-жаққа шашыраған толқындар пайда болады. Осы толқындар Ұздерімен бірге белгілі энергия мөлшерін ала кетеді де осыдан біртіндеп бастапқы жарық ағыны энергиясын азайтады. Шұғыл біртекті еместік жағдайын – ауадағы сыну көрсеткіші  бөлшекті қарастырайық. мұндай бөлшектер, мысалы: өндіріс түтініндегі, күл, төздар, қалалардың ауа бассейнінде мол болады. Ауаның қаныққан булары аса суығанда пайда болатын судың майда тамшыларынан төман түзіледі. Осындай аэротозандық жүйелерден шашыраған жарықтың интенсивтігі, әдетте, бұлардың жеке бөлшектерінің шашырататын итенсивтіктерінен құралатын қосынды болады. Аэротозаң қабаты қалың болғанда ғана көп қайтара шағылуды ескеру қажет, яғни бір бөлшектен шашыраған жарық жүйе аумағынан шыққанша басқа бөлшектермен қайта шашырау мүмкіндігін ескеру қажет.Жеке бөлшектен жарықтың шашырау сипаты оның  радиусы (біртекті еместік радиусы) мен  толқын ұзындығы арасындағы қатынасқа тәуелді болады.  болғандағы үлкен бөлшектер үшін бөлшек бетінің әртүрлі бөліктеріне түсетін жарық бұлардан әртүрлі бұрыштармен шағылады (7.21-с урет). Іс жүзінде ірі бөлшектің алдыңғы бетіне түсетін жарықтың бәрі жан-жаққа шашырайды деп санауға болады. Мөлшерлері толқын ұзындығымен шамалас ( ) бөлшектер үшін, осы біртекті еместіктерден жарықтың дифракциясы нәтижесінде пайда болатын шашырау негізгі болады (дифракциялық шашырау). Өте кіші бөлшектерден ( ) шашырауды рэлейше шашырау деп атайды, өйткені шашыраудың осы түрінің теориясын алғаш Рэлей құрған болатын.Жарықтың рэлейше шашырауы. Бұл жеткілікті көп тараған және практикалық мәні зор құбылыс болып табылады. Рэлей теориясында жарықтың кішкене сфералық бөлшектерден шашырауы қарастырылады. Осы жағдайда осындай сфералық бөлшек дипольдық сәуле шығару көзі болады деп саналады. Оптикалық біртекті еместікті ортаның көлемі бойынша ретсіз үлестірілген радиусы а бірдей сфералық бөлшектер (шариктер) жасап тұр деп ұйғарылады. Шариктердің бір-бірінен қашықтықтары а–мен салыстырғанда үлкен, ал шариктердің өздері толқын ұзындыққа салыстырғанда кіші деп алынады. Сонда шарик ішіндегі электр өрісін есептегенде Е0 сыртқы жарық толқынының өрісін біртекті деп санауға болады. Тиісті есептеулер нәтижесінде шашыраған жарық интенсивтігі үшін мына дай нәтижелер алынады (Сивухин Д.В. Общий курс физики. т. ІV. Оптика. – М.: Наука, 1980): Түсетін жарық сызықты поляризацияланған деп ұйғарылғанда шашыраған жарық та сызықты поляризацияланған болатындығы және электрлік вектор дипольдың осі арқылы өтетін жазықтықта жататындығы көрсетіледі. Мұнда және бұдан кейін де жарық интенсивтігі деп Пойнтинг векторының уақыт бойынша орташаланған мәні ұғынылады. Сонда бір сфералық бөлшектің (шариктің) шашыратқан интенсивтігі үшін мына өрнек алынады: 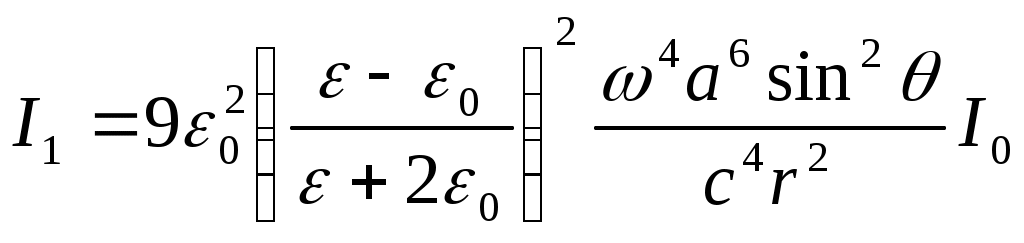 , (7.43)немесе 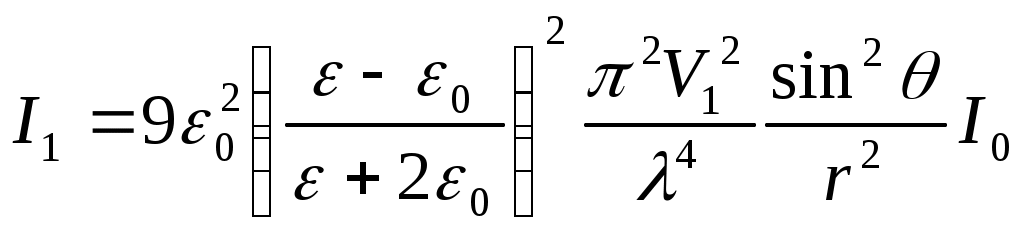 , (7.43а)мұндағы  - түсетін жарық интенсивтігі, -вакуумдағы толқын ұзындығы,  - шашыратқыш бөлшектің көлемі,  -шариктің диэлектрлік өтімділігі,  - шашыратқыш бөлшектерді қоршаған ортаның диэлектрлік өтімділігі,  - дипольдың центрінен бақылау нүктесіне дейінгі қашықтық.Сфералық бөлшектің бірлік уақытта барлық бағыттар бойынша шашырататын 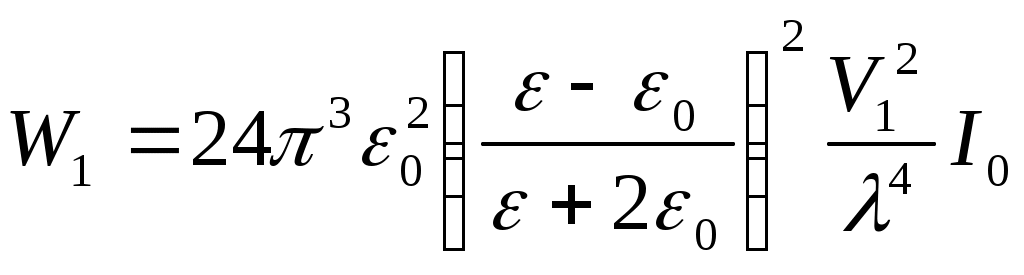 энергиясы (7.43а) шамасын радиусы сфера бойынша интегралдағанда табылады.  бет элементі ретінде алынғанда үшін мына өрнек шығады: . (*)Түсетін жарық табиғи болғанда (7.43а) орнына мына өрнек шығады:  . (7.43б)Енді шашыраған жарық шала поляризацияланған болады. Толық сызықты поляризациялану бақылау бағыты түсетін жарықтың таралу бағытына перпендикуляр болатын жағдайларда ғана байқалады, өйткені осы жағдайда бұл бағытта диполь сәуле шығармайды. Енді өте көп шариктер бар 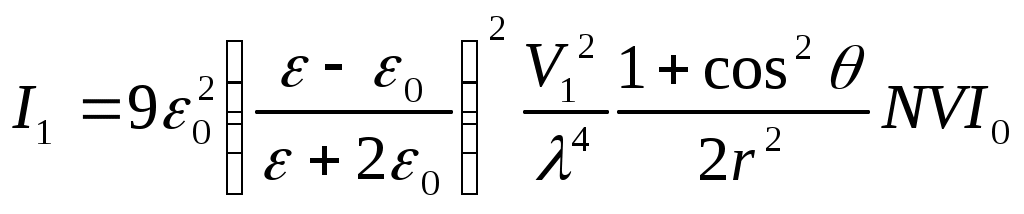 көлемнің шашырататын жарықтың  интенсивтігін табайық. Осы көлемдегі шариктердің орташа саны  , мұндағы  - бірлік көлемдегі шариктердің орташа саны. Шариктердің ара қашықтықтары толқын ұзындығымен салыстырғанда өте үлкен және олар көлем бойынша ретсіз орналасатындықтан, -ді табу үшін жеке шариктердің шашырататын интенсивтіктерін қосу керек. көлемнен бақылау нүктесіне ейінгі қашықтық көлемнің өзінің сызықтық мөлшерімен салыстырғанда өте үлкен деп ұйғарайық. Сонда (7.43б) формуладағы барлық қашықтықтарды бірдей деп санауға болады да мына өрнекті жазуға болады: . (7.43в)Түсетін жарық интенсивтігінің шашырау салдарынан кемуін есептейік. Ортадан көлденең қимасының ауданы бірге тең, ал жасаушылары z-ке параллель цилиндрді бөліп алайық. Бұдан  және  жазықтықтармен шектелген шексіз қысқа цилиндрді бөліп алайық. Осындай цилиндрдің бірінші табанынан әр секунд сайын  энергия кіреді, ал екінші табаны арылы  энергия шығады. Осы энергиялардың  айырмасы шашыраған  энергия болады. Екі өрнекті теңестіріп, мынаны аламыз: ,мұнда (*) өрнегіне сәйкес 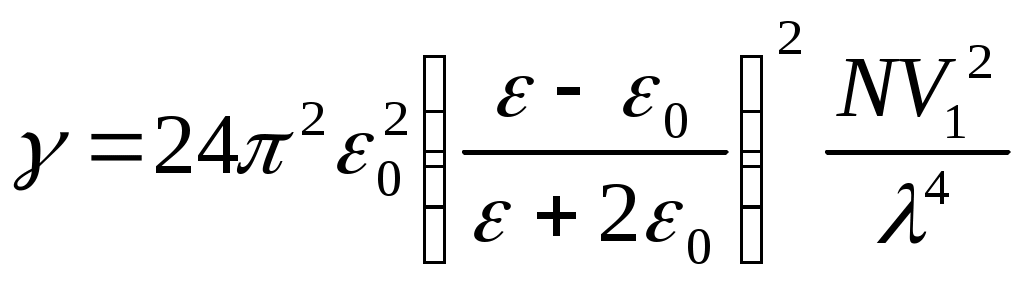 .Сонымен, шашырау салдарынан түсетін толқын интенсивтігі экспоненциалдық кемиді:  (**) шамасы шашырау коэффициенті деп аталады.(7.43а)-(7.43в) Ұрнектері Рэлей формуласы деп аталады. Осы формуланы талдау нәтижесінде рэлейше шашыраудың мынандай өзіне тән ерекшеліктері алынады. Шашыраған жарық интенсивтігінің толқын ұзындығынан тәуелділігі. Рэлей формуласынан ортаның шашыратқан жарық интенсивтігі толқын ұзындығының төрт дәрежесіне кері пропорционал (жиіліктің төрт дәрежесіне тура пропорционал) болатындығы келіп шығады. Осы нәтиже Рэлей заңы деп аталады (1871ж. тағайындалған), ол қысқарақ толқындар Ғзынырақ толқындарға қарағанда күштірек шашырайтындығын көрсетеді. Бұған мына тәжірибеге қарап көз жеткізуге болады (7.20а-сурет). Егер қарқынды ақ жарық шоғын бұлдыр сұйықтықпен толтырылған тік төртбұрышты кюветаға бағыттаса (мысалы, бірнеше тамшы сүт қосылған суға), онда осындай кюветадағы жарық шоғының ізі жақсы көрінеді. Бастапқы түсетін шоққа перпендикуляр бағытта бақылағанда шашыраған жарықтың түсі ақшыл-көгілдір болады, яғни ол  жарық көзі жарығына қарағанда қысқа толқындарға салыстырмалы бай келеді. Қысқа толқынды бөліктің қарқынды шашырауынан, Өткен шашырамаған жарық шоғы (В бағытында) салыстырмалы түрде ұзын толқынды сәулелермен байытылған болады да жарық қызғылт түсті болады.Осындай эффектілер жарық атмосферада шашырағанда байқалады. Шашыраған жарық интенсивтігі жарық тербелістері жиілігінің төрт дәрежесіне пропорционал болуынан спектрдің көк-күлгін бөлігі (және ультракүлгін бөлігі) қызылға қарағанда едәуір көп шашырайды. Күннен тура таралатын жарық атмосфера арқылы Өткенде, көк-күлгін сәулелердің қарқынды шашырауы салдарынан бұлар азаяды да, қызыл рең қабылдайды. бұл Күн шығарда және батарда, жарық сәулелері атмосфераның қалыңдау қабатынан өтетін жағдайда бақыланады. Аудағы су тамшыларының мөлшері артқанда, бұлар спектрдің әртүрлі бөліктерін бірдей дерлік шашырататындықтан, аспан түсі бозғылт тартады-көк түс әлсірейді. Егерде су тамшылары ірі болса, бұлттардағы және төмандағы сияқты, онда олар спектрдің барлық бөліктерін бірқалыпты шашыратады, сондықтан бұлттар мен төман ақ түсті болады. 2. Фотоэффект құбылысы. Эйнштейн теңдеуі. Фотоэффект үшін Эйнштейн теңдеуі. Фотоэффекті түсіндіру үшін Эйнштейн мынадай ұйғарым жасады (1905 ж): жарық толқынының энергия ағыны үздіксіз емес, ол квант немесе фотон деп аталатын энергияның дискреттік үлестерінің ағыны болып табылады. Жиілігі жарыққа сәйкес келетін фотон энергиясы  (9.34)болады, мұндағы  =1,0510-34Джс.Фотон металдағы электронмен соқтығысып, оған өзінің барлық энергиясын береді. Еркін электронмен соқтығысқан кезде оған фотонның барлық энергиясының берілуі мүмкін емес (§1.5 қараңыз). Металдағы электрөткізгіштікті қамтамасыз ететін электрондар еркін электрондар деп аталады, бірақ олар өзара бірімен-бірі және кристалдық тордың басқа электр зарядтарымен әсерлеседі. Сондықтан олар динамикалық мағынада байланысқан электрондар болып табылады және фотонның бүкіл энергиясын толығынан жұта алады. Егер осы жұтылған энергия жеткілікті үлкен болса, онда электрон өзін металда ұстап тұратын күштерді жеңеді де металдан босап шыға алады. Әрине осы процесте энергияның сақталу заңы орындалады, оны мына түрде жазуға болады  , (9.57)мұндағы  - электронның металл көлемінде ұстап тұратын күшті жеңіп және көлем аумағынан шыққан кездегі ең үлкен кинетикалық энергиясы; А- шығу жұмысы (электронды металл көлемінде ұстап тұратын күштерді жеңу үшін электронның атқарған жұмысы). (9.57) қатысы фотоэффект үшін Эйнштейн теңдеуі деп аталады.(9.34) және (9.57) теңдеулері фотоэффектің барлық ерекшеліктерін толығынан түсіндіреді. Жарық ағыны энергиясының тығыздығы (жарық интенсивтілігі) фотон ағыны тығыздығына, яғни ағынның 1 м2 көлденең қимасынан 1с ішінде өтетін фотон санына тура пропорционал. Уақыт бірлігінде жұлынып шығарылған электрон саны фотон ағыны тығыздығына тура пропорционал. Осыдан металл көлемінен уақыт бірлігінде ұшып шығатын электрон саны жарық интенсивтігіне тура пропорционал екендігі келіп шығады (фотоэффектің 1-заңы). (9.57) теңдеуге сәйкес фотоэлектронның кинетикалық энергиясы катодтан электронды жұлып шығаратын фотон энергиясына ғана тәуелді де басқа қанша фотонның басқа электрондармен соқтығысқандығына тәуелді болмайды, яғни жарық интенсивтігіне тәуелді емес (фотоэффектің 3-заңы). (9.57) теңдеуден фотон энергиясы электронның металдан шығу жұмысынан кем болған жағдайда фотоэффектің мүмкін еместігі көрінеді. Фотоэффекте қызыл шекарасының болуы осылай түсіндіріледі (фотоэффектің 2-заңы). |