ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. СДВИГ. 8. простые виды сопротивления. Сдвиг

• Название: 8. простые виды сопротивления. Сдвиг
• Анкор: ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. СДВИГ
• Дата: 03.04.2021
• Размер: 159.67 Kb.
• Имя файла: lek_08.docx
• Тип: Документы; #190840

8. ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. СДВИГ

1. 
   Определение внутренних усилий при сдвиге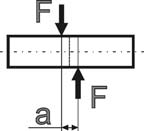
   

Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противо- положные стороны.

Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п. Вообще же на практике сдвиг в чистом виде получить трудно, так как обычно деформация сдвига сопровождается другими видами дефор- маций и чаще всего изгибом.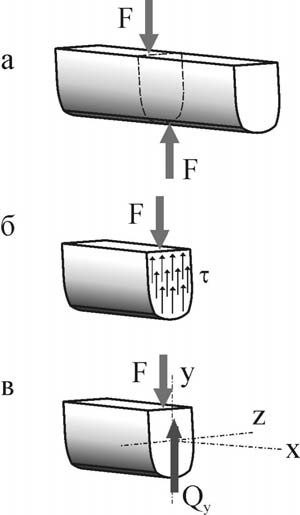

Установим формулы для внутренних усилий, на- пряжений и деформаций, необходимые при расчете на сдвиг элементов конструкций, имеющих форму бруса. Пусть известна внешняя нагрузка F, вызы- вающая сдвиг одной части бруса относительно дру- гой. Используя метод мысленных сечений (см. ри- сунок), находим величину внутренних усилий, дей- ствующих в сечении бруса. Очевидно, что в данном случае нагружения из шести уравнений равновесия лишь одно не обращается тождественно в ноль:

_ F_y 0  Q_y F.
Таким образом, при сдвиге из шести внутренних усилий (N, Q_y, Q_z, M_x, M_y, M_z) в сечении элемента конструкции возникают только одно – поперечная сила (Q_yили Q_z). N – продольное усилие; Q – поперечные усилия, M – изгибающий момент.

2. 
   Определение напряжений при сдвиге. Понятие о чистом сдвиге
   

Так как поперечная сила Q_y(или Q_z) является единственным внутренним усилием, возникающим в сечении стержня при сдвиге, и при этом она лежит в плоскости этого сечения, то и напряжения, возникающие здесь, должны лежать в плоскости сечения стержня. То есть при сдвиге в точках поперечно- го сечения стержня возникают только касательные напряжения .

касательные напряжения , действующие в поперечном сечении (A) бруса, представляют собой интенсивность внутренних поперечных сил

 ^dQ,

dA

исходя из чего можем записать (опуская соответствующие индексы):

Q _  dA.

A
При сдвиге условно считают, что касательные напряжения равномерно рас- пределены по площади поперечного сечения (=const), поэтому

Q  A.
Тогда касательные напряжения при сдвиге определяются так:

 ^Q

   ^F.

(8.1)

A A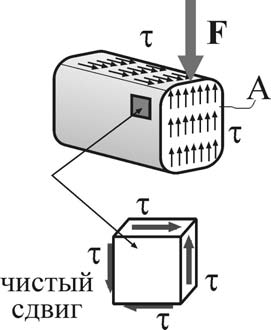

Рассмотрим характер напряженно-деформированного состоя- ния, которое возникает в точках стержня при сдвиге.

По закону парности касательных напряжений в про- дольных сечениях бруса, так же как и в его попереч- ных сечениях будут возникать только касательные напряжения. Тогда на гранях (параллельных соответ- ствующим осям координат) бесконечно малого эле- мента, «вырезанного» в окрестности любой точки стержня при сдвиге, будут действовать только каса- тельные напряжения . Такой случай напряженного состояния называют чистым сдвигом .

Чистый сдвиг – частный случай плоского напряженного состояния, при ко- тором по граням прямоугольного элемента действуют только касательные напряжения.

Определим величину и направление главных напряжений при чистом сдвиге:

_{ } _x _y

 ¹  ,

1,3 _{2 2}

так как _x=_y=0, то можем записать

₁  _xy,
₃  _xy.

Направление главных площадок определяется углом , который найдем по формуле

учитывая, что _x=_y=0,

tg2 

2  _{xy ,}

_x _y

tg2    



2    

2



  .

4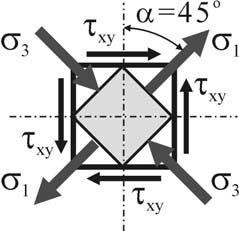

Как видим, при чистом сдвиге главные напряжения одинаковы по величине, противоположны по знаку (₁=–₃=_xy) и направлены под углом 45^о к оси стержня (третья главная площадка элемента совпадает с ненагруженной фа- садной гранью элемента, следовательно ₂=0).

3. 
   Определение деформаций и закон Гука при чистом сдвиге
   

Рассмотрим деформацию квадратного элемента при чистом сдвиге (см. рису- нок).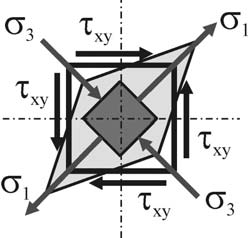



Поскольку по граням элемента не действуют нормальные напряжения, то вдоль граней нет и удлинений. В то же время диагональ, совпадающая с на- правлением ₁, удлинится, а другая диагональ, совпадающая с направлением сжимающего напряжения ₃, укоротится. В результате квадрат трансформи- руется в ромб без изменения длины граней. Таким образом, деформация чис- того сдвига характеризуется изменением первоначально прямых углов.
Более наглядное представление о деформации элемента при сдвиге можно получить, закрепив одну из граней (см. рисунок).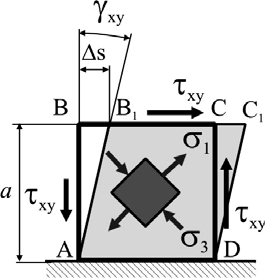

Малый угол _xy, на который изменяется первоначально прямой угол элемента при сдвиге, называется углом сдвига или относительным сдвигом:

 _xy BAB₁ .
Величину абсолютного смещения грани обозначают sи называют абсолют- ным сдвигом.

Из треугольника BAB₁ следует, что

tg  ^s.



xy _a

Учитывая малость угла, можно считать, что

tg _xy  _xy,

тогда окончательно запишем взаимосвязь между относительным и абсолют- ным сдвигом элемента

  ^s. (8.2)



xy _a
Зависимость между нагрузкой и деформацией при сдвиге можно проследить по так назы- ваемой ди агр а мме сдвиг а , которую получают обычно из опытов на кручение тон- костенных трубчатых образцов (в стенках которых, как увидим далее, также возникает напряженное состояние чистого сдвига). Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения и имеет с ней одинаковые характерные участки, в том числе и участок упругости.

Рассматривая деформацию сдвига в пределах упругости, найдем, что между углом сдвига _xyи касательными напряжениями _xyсуществует линейная за- висимость, которая носит название закона Гука при сдвиге и может быть вы- ражена следующими формулами:

  ^xy, или

xy _G

_xy G  _xy, (8.3)

где G – коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода и является константой для данного материа- ла. Модуль сдвига может быть определен аналитически, если известны величины модуля Юнга и коэффициента Пуассона:

G  ^E .

2  _1  _

Заметим, что все рассмотренные характеристики упругости материала E, , G, K взаимо- связаны, однако в сопротивлении материалов и в теории упругости только две из них (ча- ще всего Eи ) принимаются независимыми.
Подставляя выражения (8.1) и (8.2) в формулы (8.3), можно записать закон Гука при сдвиге и во «внешних формах» (через абсолютные деформации и внутренние усилия):

s= ^{Q a},

G A

где a– расстояние между сдвигаемыми гранями; A– площадь грани.

Удельную потенциальную энергию деформации (см. лекцию № 6) при сдвиге

определим, учитывая, что

₁  _xy,

₃  _xy, следующим образом:

1 2 3 1 2 2 3 3 1
u  ¹ 2  E

 ^_²  ²  ²  2   _        _^_ 

_u 2 _1_{  2 }

2  E

_2

2  G^.

4. 
   Расчет на прочность и допускаемые напряжения при сдвиге
   

Проверим прочность элемента, испытывающего деформацию чистого сдвига. Пусть каса- тельные напряжения на гранях элемента максимальны и равны _max, а допускаемое напря- жение для материала при растяжении – [].

Если для материала известна величина допускаемых касательных напряже- ний при сдвиге [], то условие прочности может быть записано в виде:

_{ } ^Qmax

 __ . (8.4)

max _A

Величина допускаемых напряжений [] зависит от свойств материала, харак-

тера нагрузки, типа элементов конструкции и для чистого сдвига определяет- ся обычно по III теории прочности:

^экв

III

 __.

Учитывая, что по III теории прочности

а при чистом сдвиге

^экв

III

 ₁  ₃ ,

можем записать или

₁  ₃  _max,

_max __max  __ ,

  ^ . (8.5)

max ₂
Сравнивая выражения (8.4) и (8.5), заметим, что по III теории прочности

__  ^ .

2
Полученную величину допускаемых касательных напряжений [] используют при расчетах на прочность деталей, испытывающих деформацию сдвига, в соответствии с условием прочности (8.4).