|
|
электростатика 24. 8. работа сил электростатического поля
8. работа сил электростатического поля
Вычислим работу, которую совершает электростатическое поле, созданное зарядом q’ по перемещению заряда q из точки 1 в точку 2
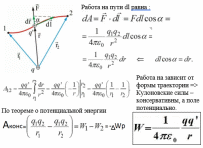
-потенциальная энергия заряда q, находящегося в поле созданном точечным зарядом q’. Разделим это выражение на q:
- не зависит от q и является энергетической характеристикой элекрич. поля и газывается
потенциал – с.ф.в, характеризующая энергетическое состояние поля в данной точке. Потенциал поля,
созданного точечным зарядом:
Т.о. работа, совершаемая силами электрического поля при перемещении заряда = произведению величины этого заряда на разнось потенциалов начальной и конечной точек. Если перемещать заряд из т. с потенциалом φ за пределы поля, т.е. в
Потенциал – с.ф.в, определяемая работой по перемещению единичного «+» заряда при удалении его из данной точки в
Потенциал -величина алгебраической (мб + и -). Если поле создано несколькими зарядами, по потенциал поле системы зарядов = алгебраической сумме потенциалов полей всех зарядов. Принцип суперпозиции для потенциалов электростатического поля:
9. Циркуляция вектора напряженности
Из формулы работы хорошо видно, что работа по замкнутому контуру равна 0:
Интеграл называется циркуляцией
вектора напряженности. Т.о. циркуляция
 вектора напряженности электростатичес-
 кого поля (Е) = 0
|
  10.Связь между
 Е - силовая характеристика, а φ - энергет. характеристика эл. Поля
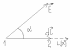
Работа при перемещении заряда Q
|
В направлении Е потенциал уменьшается.
Если поле однородно
- связь эл.поля
|
11. Проводникик в электростатическом поле.
Проводникики – в-ва, проводящие эл.ток, т.е. в них имеются свободные заряды, которые способны перемещаться по проводнику под действием внешнего электрического поля. В металлических проводниках это электроны, они образуют газ, заполняющий кристаллическую решетку, состоящую из «+» заряженных ионов.
При внесении металлич.проводника
Во внешние электростатическое поле,
Электроны проводимости перемещаются
(перераспределяются) до тех пор, пока
Всюду внутри проводника поле электронов
проводимости и положительных ионов не
скомпенсирует внешнее поле. В любой точке
внутри проводника, находящимся в электрост.
поле Е=0;
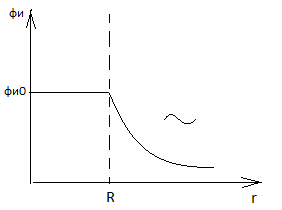
Найдем потенциал сферического проводника
|
12.Электроемкость уединенного проводника.
Уединенный проводник – проводник, удаленный от других тел.
Из формулы потенциала φq
Коэфф. Пропорциональности обозначим С, тогда q=С*φ
C=q/φ – электроемкость уединенного проводника, с.ф.в, характеризующая способность проводника накапливать электрический заряд.
Электроемкость не зависит от q и φ, а зависит от электрических веществ среды и от геометрического проводника.
Найдем емкость сферического проводника:
1 Фарад – это емкость такого тела, у которого
при увеличении заряда на 1 Кл, его потенциал
увеличивается на 1В.
Уединенный проводники обычных размеров обладают ничтожно малой емкостью и поэтому не способны накапливать большие электрические заряды. Но оказывается наличие вблизи уединенного проводника каких либо тел увеличивает его электроемкость.
Электрическое поле ослабевает Е=Е++Е-
-система из двух близко расположенных проводников, заряды которых равны по величине и противоположны по знаку, их взаимная емкость рассчитывается по формуле С=|q|/φ
Наиболее эффективней такая система становится если в качестве проводников взять параллельные пластины, или два коаксиальных цилиндра, или две концентрические сферы и называется система–конденсатор. Электроемкость конденсатора: q-заряд положительно заряженной пластины
С=q/(φ1-φ2)=q/U U-разность потенциалов между обкладками
Электроемкость конденсатора зависит от его геометрических размеров и диэлектрических св-в среды между обкладками.
Виды конденсаторов:
1.Емкость плоского конденсатора
2. Сферический конденсатор
3.Цилиндрический конденсатор
|
Назначение конденсаторов
1.накапливать на короткое время заряд или энергию для быстрого измерения потенциала.
2.Не пропускать постоянный ток
3.В радиотехнике: колебательный контур, выпрямитель
4.Фотовспышка
13.Энергия заряженного проводника и конденсатора
Чтобы зарядить проводник, необходимо совершить работу внешними силами против кулоновских сил отталкивания, а сообщая заряд проводнику мы сообщаем ему энергию
Энергия уединенного проводника:
Аналогично можно получить формулу для энергии заряженного конденсатора. Если учесть, что С=q/φ, то:
-энергия заряженного конденсатора.
14.Энергия электростатического поля. Обьемная плотность энергии. Энергия эл.поля = энергии заряженногг конденсатора, тк когда конденсатор разряжен, то поля нет:
Для плоского конденсатора:
Обьемная плотность энергии элек-стат. поля:
| |
|
|
Скачать 0.98 Mb.