9-сынып. Геометрия 2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
А нүктесінің координаталары (3;-2) болса, ⃗а (−2; 1) векторына параллель көшіргенде алынған А, нүктесінің координатасын табыңыз.
А) (1;-1) В) (-1;2) [1] С) (-1;1) Д) (1;-2)
Ромбының неше симметрия осі болады?
А) екеу В) төртеу С) шексіз көп [1] Д) симметрия осі жоқ
Теңбүйірлі трапецияның симметрия центрі бола ма? А) иә, болады
В) жоқ, болмайды С) шексіз көп [1] Д) симметрия осі жоқ
Координаталық жазықтықта 𝑥2 + 2𝑥 + 𝑦2 − 4𝑦 + 4 = 0 теңдеуімен берілген шеңберге :
абсцисса осіне;
ордината осіне қарағанда симметриялы болатын шеңбердің сызбасын сызыңдар және теңдеуін жазыңдар. [6]
MNPK трапецияның NP және МК табандары сәйкесінше 8 және 2-ге тең. EF кесіндісі табандарына параллель және осы трапецияны екі ұқсас трапецияларға бөледі.
EF кесіндісін және ұқсастық коэффициентін табыңыз.
|
|
[ 4]
|
6. АВС және А1В1С1 үшбұрыштарында ∠А = ∠А1, ∠В = ∠В1, АВ = 4см, ВС = 6 см, АС = 3см, В1С1 = 3см.
А1В1 және А1С1 қабырғаларын және периметрін есептеңіздер.
|
|
[5]
|
7. АВСжәне DEFүшбұрыштары ұқсас болса,DEқабырғасын табыңыз.
|
[2]
|
| 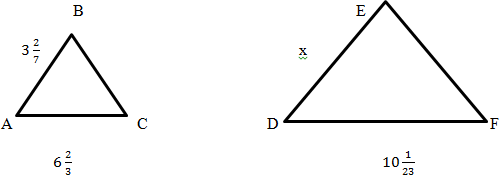
                      Балл қою кестесі Балл қою кестесі
№
|
Жауап
|
Балл
|
Қосымша ақпарат
|
1
|
А
|
1
|
|
2
|
А
|
1
|
|
3
|
В
|
1
|
|
4
|
𝑥2 + 2𝑥 + 1 + 𝑦2 − 4𝑦 + 4 = 0 + 1 (𝑥 + 1)2 + (𝑦 − 2)2 = 1 R=1; C(-1;2)
|
1
|
(𝑥 − а)2 + (𝑦 − в)2 = 𝑅2
формуласын қолданады
|
Сызбаны сызады
|
1
|
|
4а
|
абсцисса осіне қатысты симметриялы шеңберді сызады. R=1; Центрі C(-1;-2) нүктесі
|
1
|
|
Шеңбер теңдеуін жазады:
(𝑥 + 1)2 + (𝑦 + 2)2 = 1
𝑥2 + 2𝑥 + 1 + 𝑦2 + 4𝑦 + 4 − 1 = 0
𝑥2 + 2𝑥 + 𝑦2 + 4𝑦 + 4 = 0
|
1
|
|
4в
|
ордината осіне қатысты симметриялы шеңберді сызады. R=1; Центрі C(1;2) нүктесі
|
1
|
|
Шеңбер теңдеуін жазады:
(𝑥 − 1)2 + (𝑦 − 2)2 = 1
𝑥2 − 2𝑥 + 1 + 𝑦2 − 4𝑦 + 4 − 1 = 0
𝑥2 − 2𝑥 + 𝑦2 − 4𝑦 + 4 = 0
|
1
|
|
5
|
Сызбаны сызады
|
1
|
|
|
𝑁𝑃 = 𝐸𝐹
𝐸𝐹 𝑀𝐾
|
1
|
Үшбұрыштар ұқсастығы қасиетін қолданады
|
|
2 EF
= , EF2 = 16 EF = 4
EF 8
|
1
|
|
|
𝑘 = 𝑁𝑃 = 2 = 1
|
1
|
|
|
𝐸𝐹 4 2
|
6
|
Сызбаны сызады
|
1
|
|
1
|
|
|
|
В1С1 = 𝑘 ∙ 𝐵𝐶 , 6𝑘 = 3 , 𝑘 = 2
|
1
|
|
А В = 1 ∙ 𝐴𝐵 =2
1 1 2
|
1
|
|
|
А С = 1 𝐴𝐶 =1,5
1 1 2
|
1
|
|
|
𝑃𝐴𝐵𝐶 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 4 + 6 + 3 = 13
|
1
|
|
|
𝑃𝐴𝐵𝐶 = А1В1 + В1С1 + А1С1 = 3 + 2 + 1,5 = 6,5
|
1
|
|
7
|
2 2
𝐴𝐵 𝐴𝐶 3 6
= ; 7 = 3
𝐷𝐸 𝐷𝐹 𝑥 10 1
23
|
1
|
Үшбұрыштар
|
|
|
ұқсастығын қолданып
|
|
|
пропорция құрады
|
|
23 231 20 3 99 19
𝑥 = 7 ∙ 23 : 3 = 33 ∙ 20 = 20 = 4 20
жауабы: 𝑥 = 4 19
20
|
1
|
Пропорцияның белгісіз
|
|
мүшесін табады
|
|
Барлығы
|
20
|
| |
 Скачать 20.07 Kb.
Скачать 20.07 Kb.





















 Балл қою кестесі
Балл қою кестесі