математикадан республикалы0 олимпиаданы4 облысты0 кезе43. Матем Республикалық олим облыстық кезеңі. 9 сынып Задача 2
 Скачать 26.62 Kb. Скачать 26.62 Kb.
|
|
9 сынып Задача № 2. Треугольник АВС удовлетворяет следующему условию: на отрезке ВС существует единственная точка Х такая, что АХ2 = ВХ * СХ. Докажите , что АВ + ВС = ВС 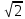 Шешуі: 1) АВСД шаршысын шеңберге іштей сызамыз. Кез – келген АВС тікбұрышты үшбұрышы үшін АХ2 = ВХ * СХ шарты орындалады. Егер 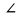 ВАД = ВАД = 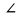 ДАС болса, онда АВ + АС = ВС ДАС болса, онда АВ + АС = ВС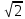 және ВХ = СХ , АХ = ДХ, АД - биссектриса, олай болса АД АВС тікбұрышты емес үшбұрыш үшін де биссектриса болсын деп қарастырайық. және ВХ = СХ , АХ = ДХ, АД - биссектриса, олай болса АД АВС тікбұрышты емес үшбұрыш үшін де биссектриса болсын деп қарастырайық. 2) Қандай да бір АВДС дөңес төртбұрышы шеңберге іштей сызылған. 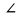 ВАД = ВАД = 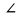 ДАС, АХ = ДХ. ДАС, АХ = ДХ. 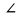 ВХА ВХА 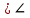 ДХС, ДХС, 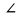 ВАХ = ВАХ = 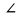 ДСХ, ДСХ, 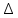 АВХ ұқсас АВХ ұқсас 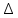 ДСХ. ДСХ. 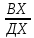 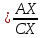 = = 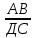 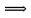 АВ = АВ = 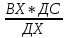 , ВХ*СХ = ДХ*АХ, ал ДХ= АХ болғанда есеп шарты орындалады, яғни АХ2 = ВХ * СХ , ВХ*СХ = ДХ*АХ, ал ДХ= АХ болғанда есеп шарты орындалады, яғни АХ2 = ВХ * СХ 3) СДХ = 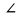 СДА, СДА, 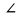 ДСХ ДСХ 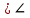 ДАС, ДАС, 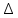 ДСХ ұқсас ДСХ ұқсас 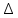 АДС. АДС. 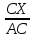 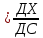 = = 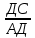 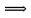 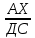 = = 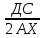 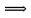 ДС = ДС = 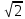 АХ. Олай болса, АС АХ. Олай болса, АС 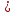 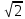 СХ, АВ СХ, АВ 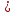 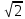 ВХ, демек , АВ + АС ВХ, демек , АВ + АС 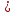 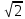 (ВХ + СХ) (ВХ + СХ)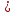 ВС ВС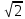 . . Задача №6. На плоскости нарисован четырехугольник АВСД . Докажите, что на этой плоскости найдется такая точка Х, что квадрат расстояния от точки Х, до самой удаленной от неё вершины треугольника АВСД, не превосходит 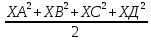 Шешуі: І тәсіл. 1) ХА2 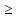 а2, ХВ 2 а2, ХВ 2 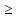 2а2, ХС2 2а2, ХС2 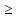 3а2 және ХД2 3а2 және ХД2 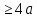 2 болсын. 2 болсын. 2) 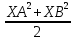 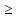 ХА*ХВ ХА*ХВ 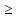 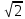 а2 , а2 , 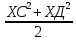 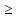 ХС*ХД ХС*ХД 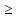 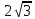 а2 а23) 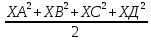 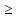 ( ( 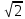 + + 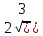 а2 а2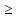 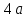 2 2Шешуі: ІІ тәсіл. ХА = ХВ = а , ХС = 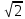 а және ХД = 2а болатындай кез – келген АВСД төртбұрышын саламыз. Сонда , а және ХД = 2а болатындай кез – келген АВСД төртбұрышын саламыз. Сонда , 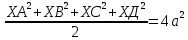 2) ХА 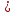 а , ХВ а , ХВ 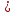 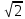 а , ХС а , ХС 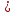 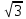 а және 2а а және 2а 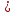 ХД ХД 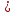 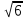 а болатындай кез – келген АВСД төртбұрышын саламыз Бұдан, а болатындай кез – келген АВСД төртбұрышын саламыз Бұдан, 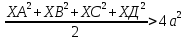 11 сынып. Задача №6. При каких натуральных n число (n – 1)! делится на n3 ? Шешуі: 1) 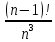 = = 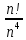 = = 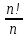 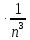 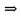 n=1 n=12) Егер n 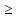 7 болса, онда n 7 болса, онда n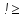 n4 , n – жай сан емес n4 , n – жай сан емесn! = 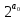 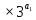 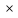 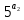 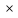 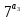 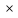 … …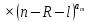 (n-R), l , R (n-R), l , R 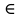 N, N, 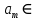 N, m N, m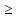 0, 0, 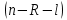 , (n - R) - жай сандар , (n - R) - жай сандар n4 = 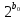 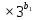 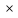 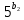 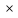 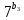 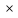 … …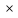 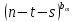 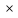 (n – t). s,t (n – t). s,t 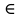 N, N, 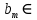 N, m N, m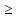 0. ( n- t – s), (n – t) - жай сандар 0. ( n- t – s), (n – t) - жай сандарn=10 болсын, 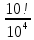 = = 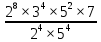 n=12, 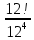 = = 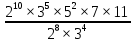 = 22 = 22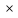 3 3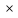 52 52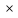 7 7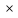 11 11n = 18 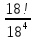 = =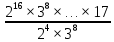 = 212 = 212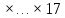 n = 20 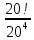 = =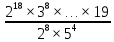 = 210 = 210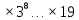 n= 24, n = 27 т.с.с. анықтауға болады Жауабы: 1 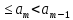 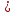 … …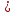 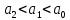 , , 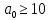 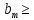 4. Егер 4. Егер 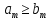 болса, онда болса, онда 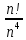 яғни яғни 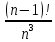 бөлінеді бөлінеді10 класс При каких натуральных n число (n – 1)! делится на 2021n2 ? Шешуі:1) 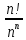 =1 онда n=1 =1 онда n=1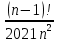 = t, t = t, t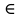 N N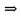 (n – 1)! (n – 1)! 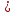 2021n2 2021n2 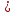 43 43 47n2 n – 1 47n2 n – 1 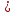 n2 ендеше n – 1 n2 ендеше n – 1 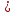 43, n 43, n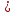 44 442) (n – 1 )! Жұп сан, демек n жай сан емес 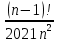 = = 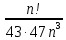 , n = 45, , n = 45,  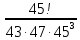 = = 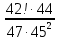 , 47 жай сан, олай болса көбейтінді , 47 жай сан, олай болса көбейтінді 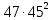 – на бөлінбейді – на бөлінбейдіn 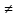 46, n 46, n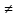 47 47n = 48, 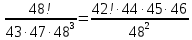 = = 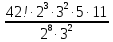 = = 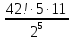 бөлінеді, өйткені 25 = 32 бөлінеді, өйткені 25 = 32n= 2021, 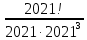 = = 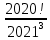 бөлінеді, бөлінеді, өйткені 43 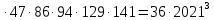 3) n! және 2021n3 сандарын жай көбейткіштерге жіктегенде негіздері бірдей жай көбейткіштердің дәрежелері n! жіктелуінде 2021n3 – ке қарағанда артық болады. Жауабы: n 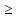 48, n жай сан емес 48, n жай сан емес |
