Математика. А найти уравнение прямой регрессии у на х

• Название: А найти уравнение прямой регрессии у на х
• Анкор: Математика
• Дата: 04.04.2022
• Размер: 152 Kb.
• Имя файла: 10281_17v-IDZ19.2.doc
• Тип: Документы; #439874

ИДЗ 19.2 – Вариант 17.

Дана таблица распределения 100 заводов по производственным средствам X(тыс. ден. ед.) и по суточной выработке Y(т). Известно, что между X и Y существует линейная корреляционная зависимость. Требуется:

а) найти уравнение прямой регрессии у на х;

б) построить уравнение эмпирической линии регрессии и случайные точки выборки (X,Y).
1.17

Y X	12000	12570	13140	13710	14280	14850	15420	15990	mx
1500	1	6	4	−	−	−	−	−	11
1600	−	−	4	7	5	−	−	−	16
1700	−	−	−	6	15	6	−	−	27
1800	−	−	−	8	8	4	−	−	20
1900	−	−	−	−	5	5	6	−	16
2000	−	−	−	−	−	5	2	3	10
my	1	6	8	21	33	20	8	3	100

Решение:

Для подсчета числовых характеристик (выборочных средних 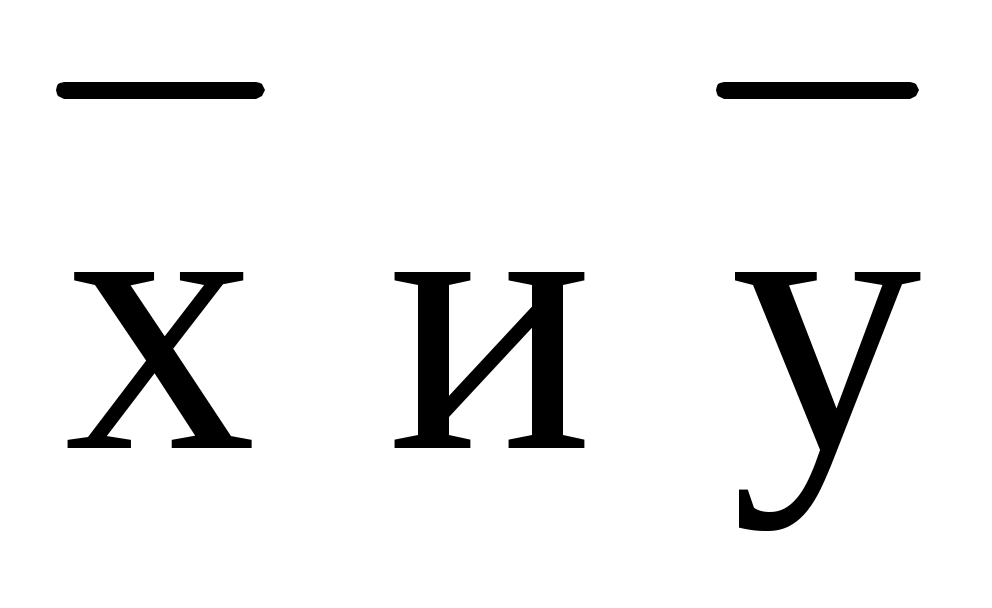, выборочных средних квадратичных отклонений s_x и s_y и выборочного корреляционного момента s_xy) составляем расчетную таблицу. При заполнении таблицы осуществляем контроль по строкам и столбцам:







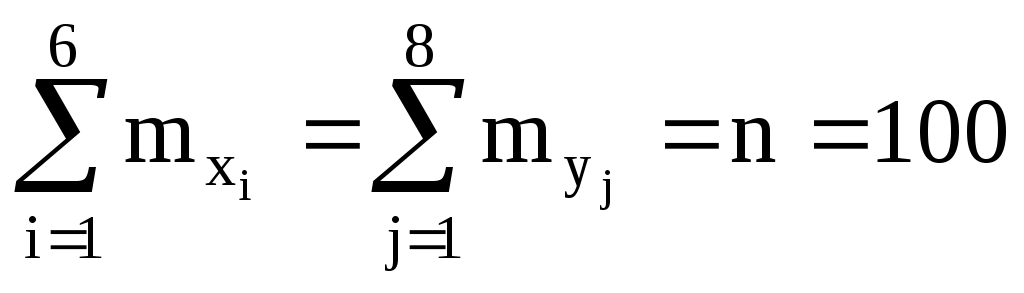
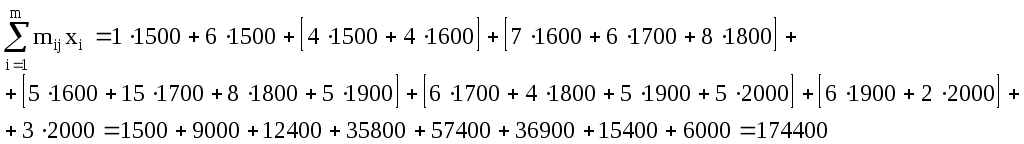
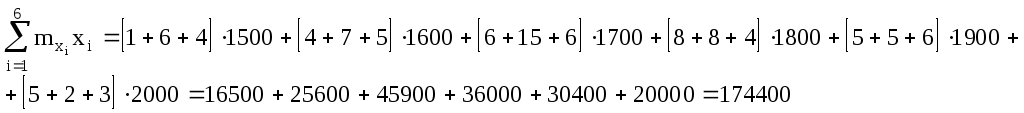
Тогда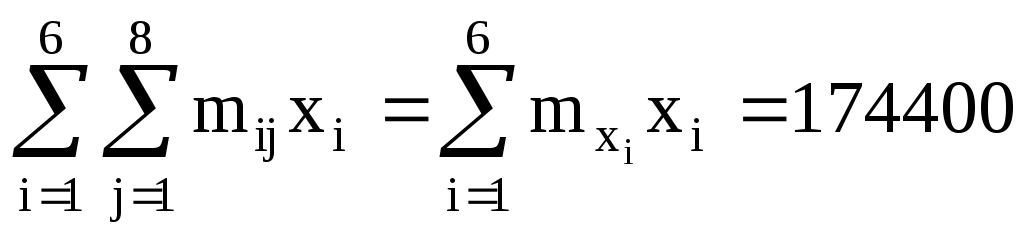




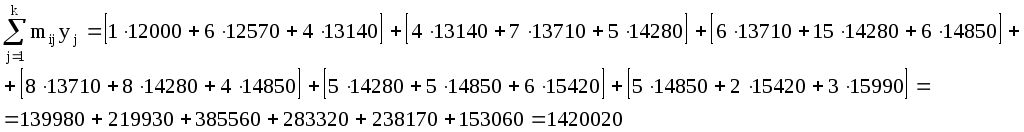
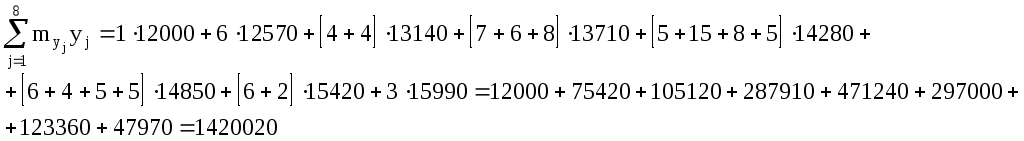
Тогда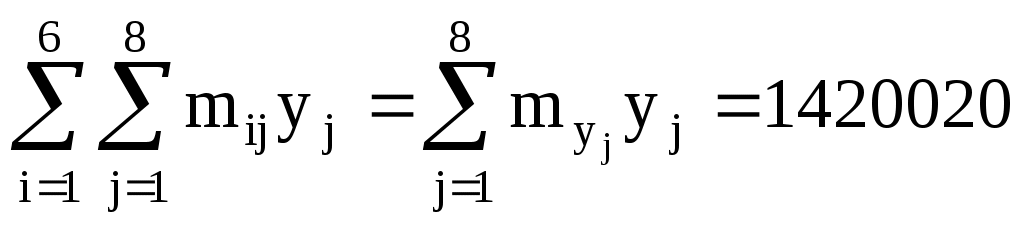

Y X	12000	12570	13140	13710	14280	14850	15420	15990	mxi	mxixi
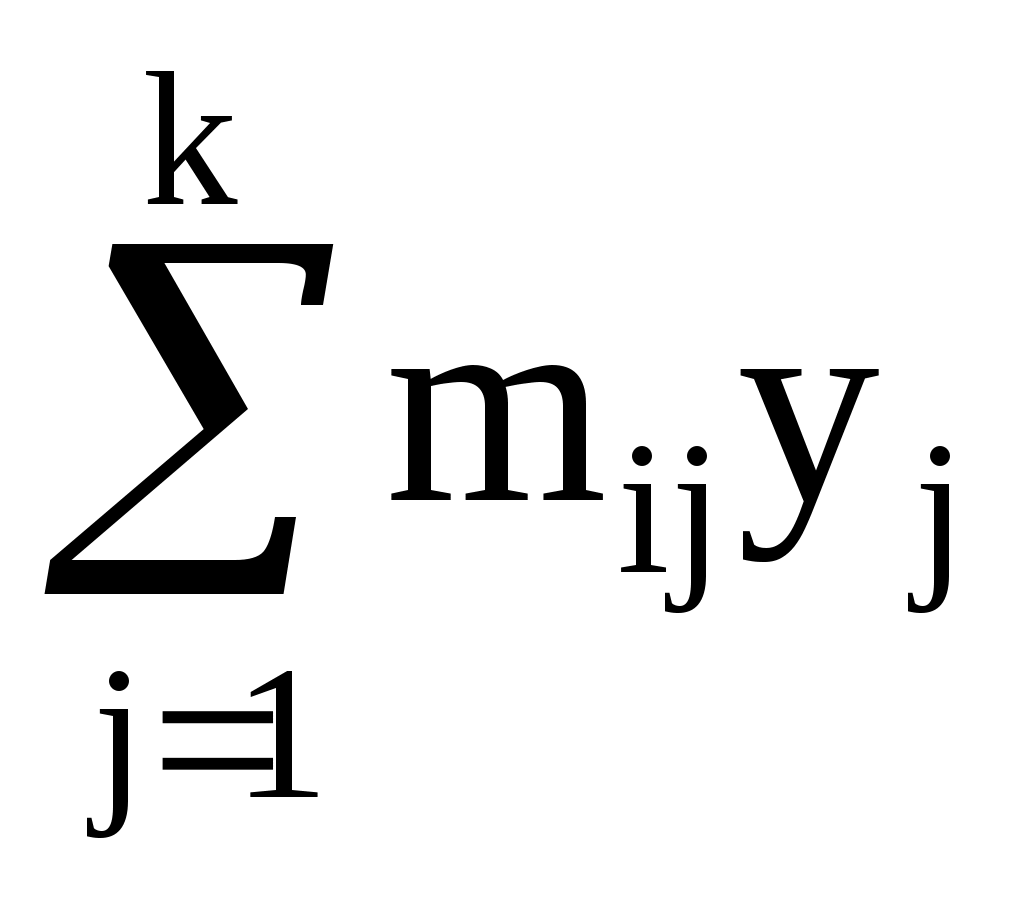
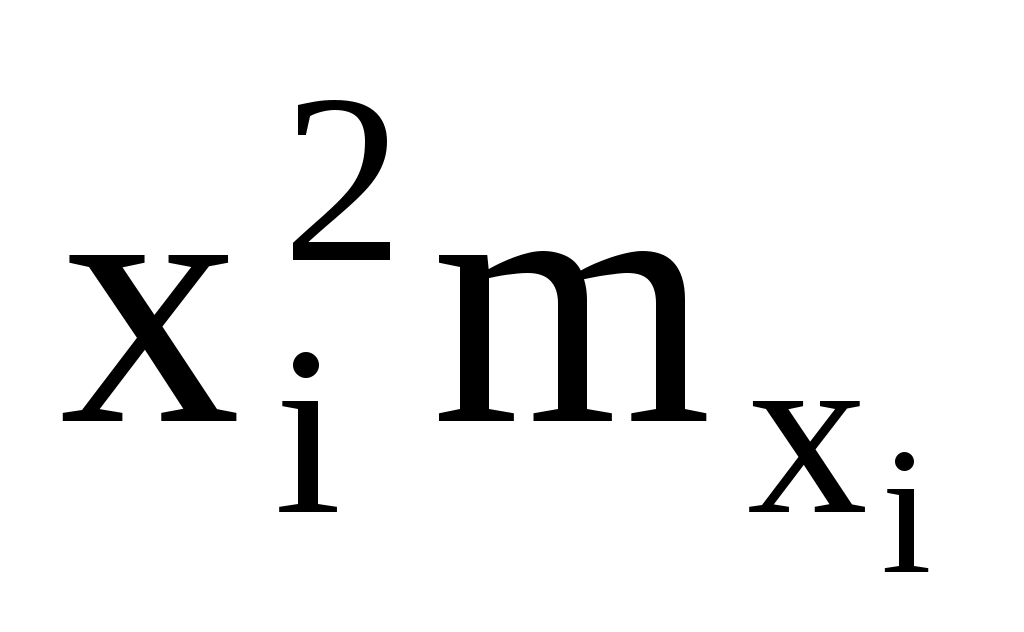
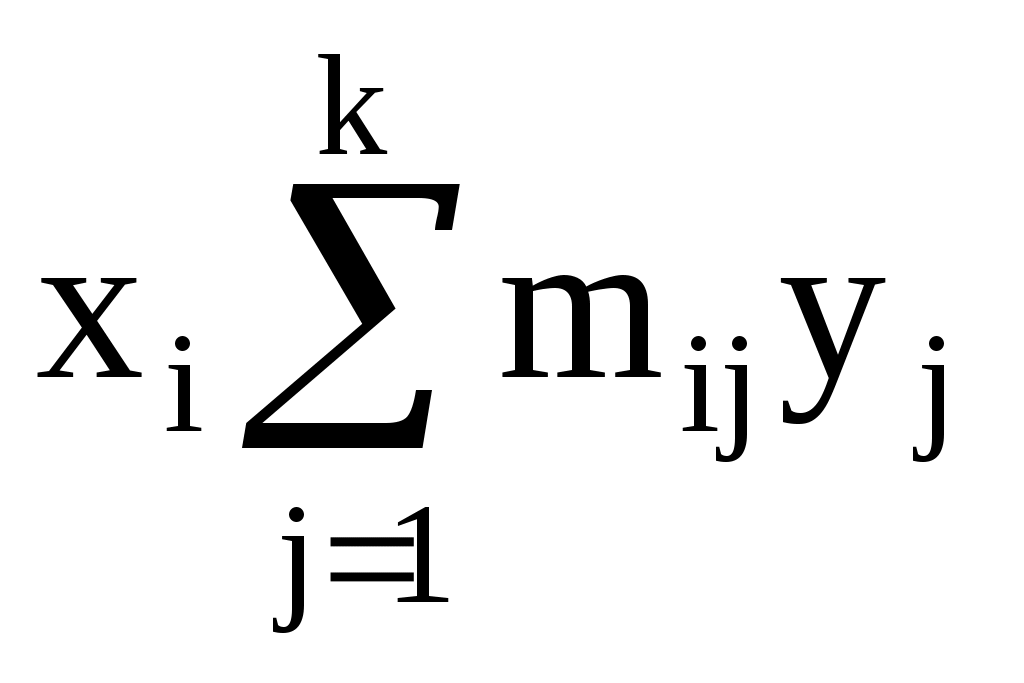
1500	1	6	4	−	−	−	−	−	11	16500	139980	24750000	209970000
1600	−	−	4	7	5	−	−	−	16	25600	219930	40960000	351888000
1700	−	−	−	6	15	6	−	−	27	45900	385560	78030000	655452000
1800	−	−	−	8	8	4	−	−	20	36000	283320	64800000	509976000
1900	−	−	−	−	5	5	6	−	16	30400	238170	57760000	452523000
2000	−	−	−	−	−	5	2	3	10	20000	153060	40000000	306120000
myj	1	6	8	21	33	20	8	3	100	174400	1420020	306300000	2485929000
myjyj	12000	75420	105120	287910	471240	297000	123360	47970	1420020	−	−	−	−
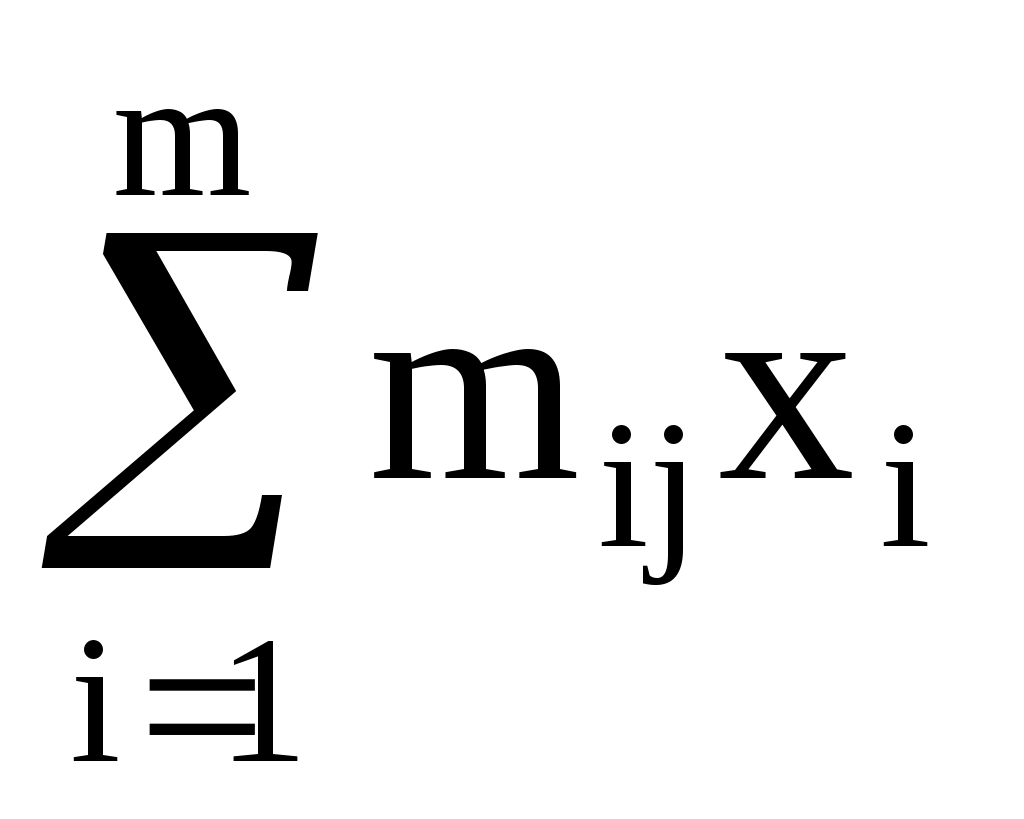
	1500	9000	12400	35800	57400	36900	15400	6000	174400	−	−	−	−
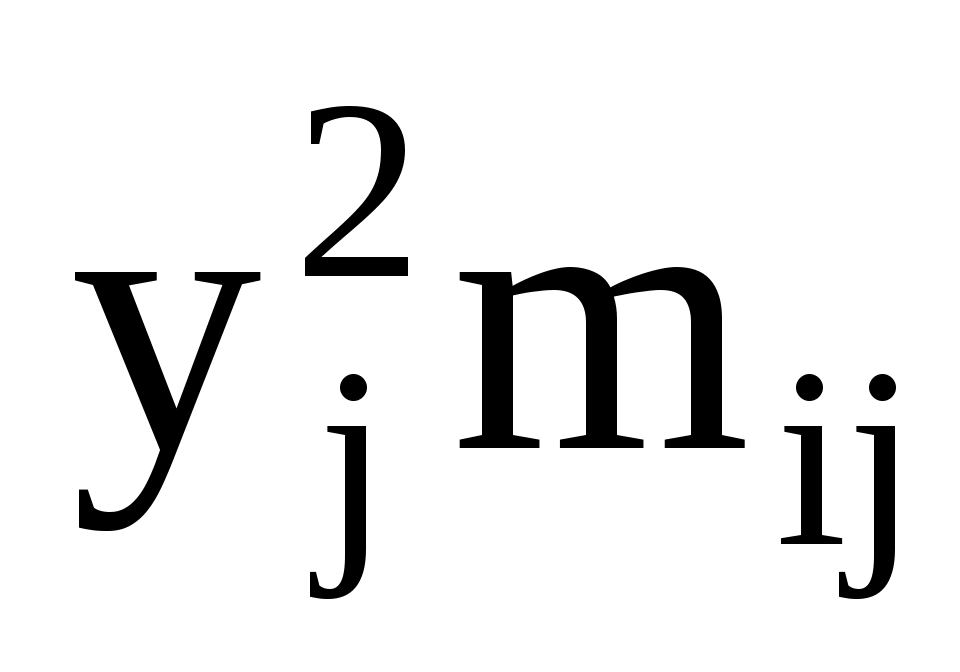
	144000000	948029400	1381276800	3947246100	6729307200	4410450000	1902211200	767040300	20229561000	−	−	−	−
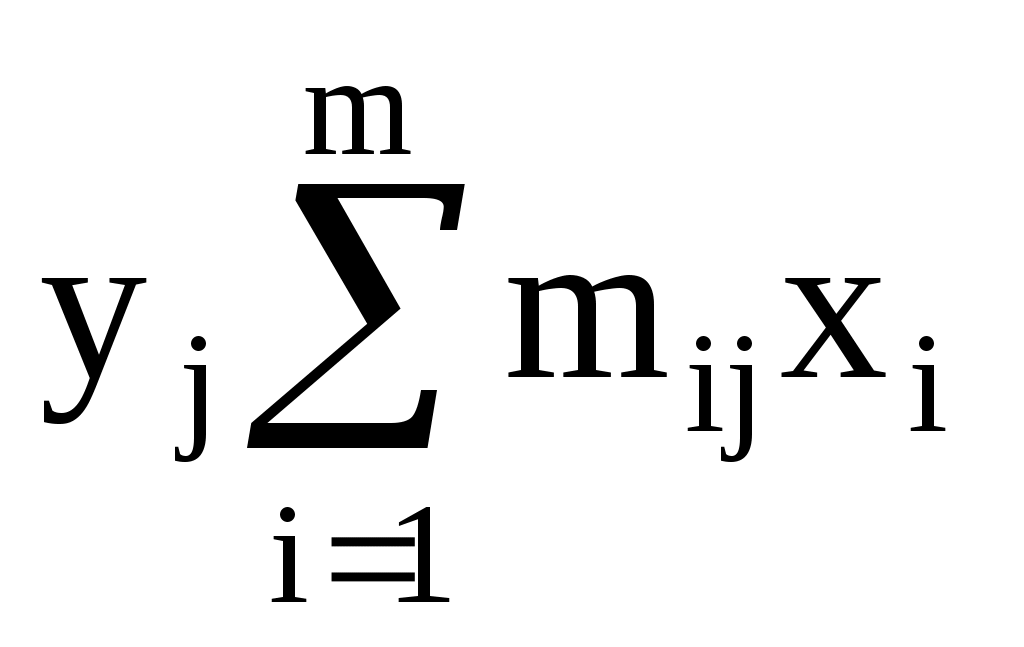
	18000000	113130000	162936000	490818000	819672000	547965000	237468000	95940000	2485929000	−	−	−	−

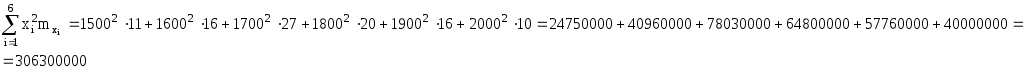
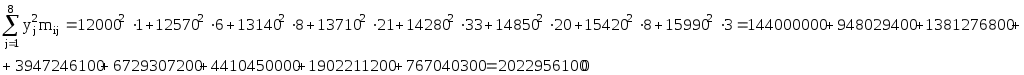
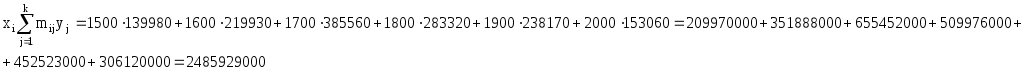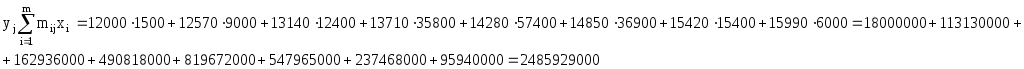
Тогда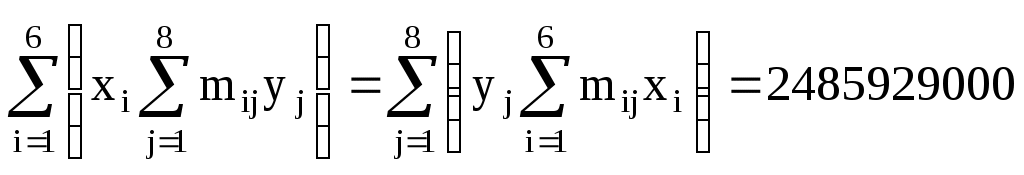
Вычисляем выборочные средние ,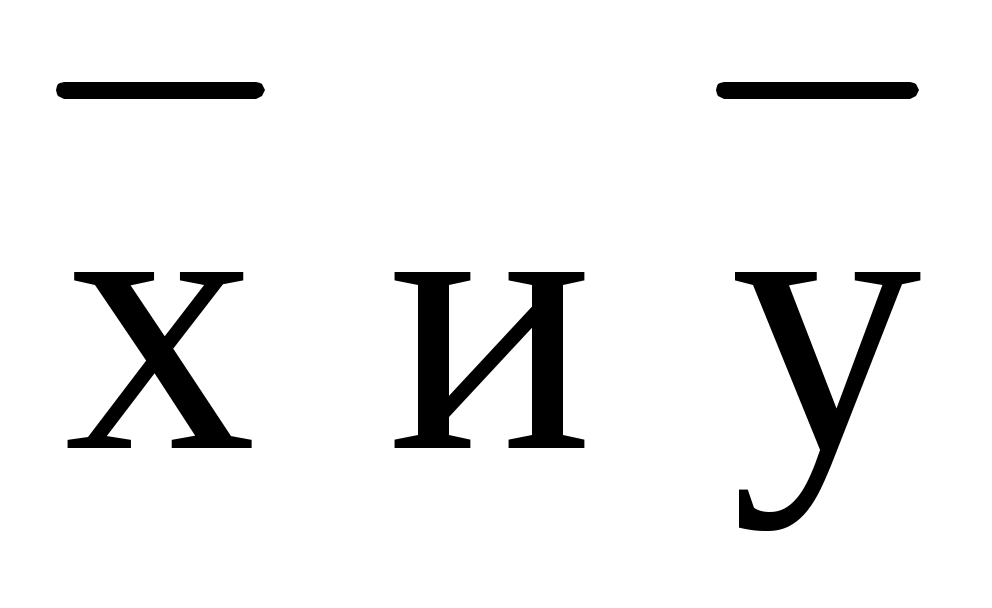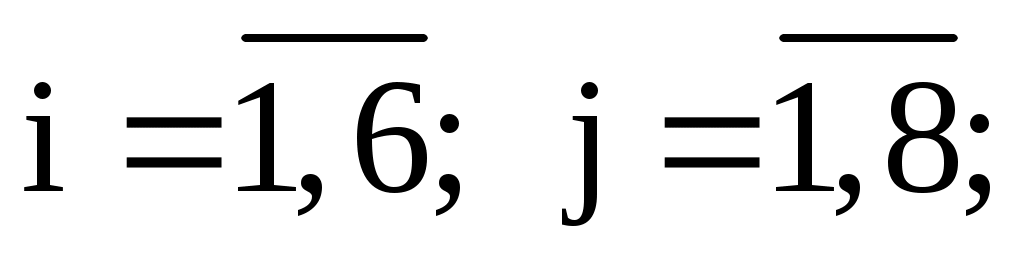





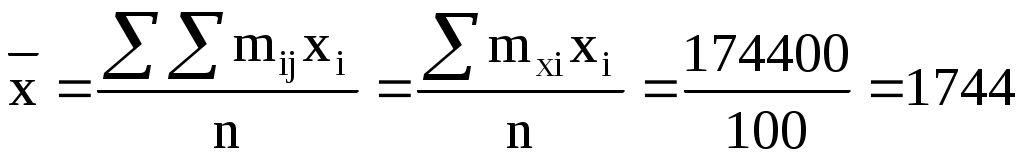
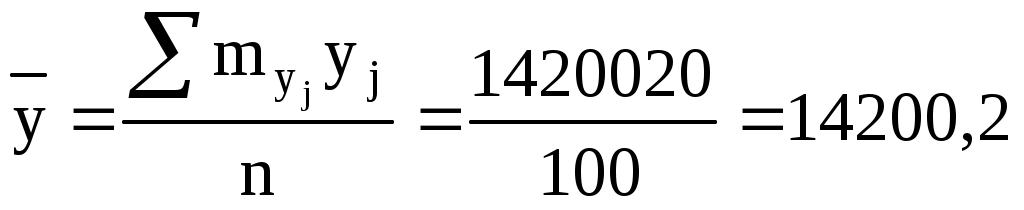
Выборочные дисперсии находим по формулам:


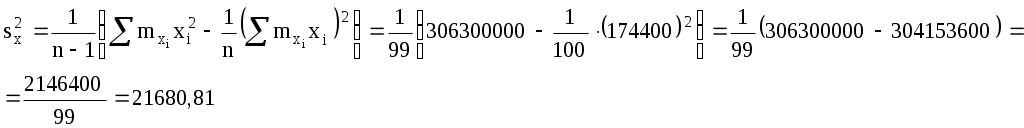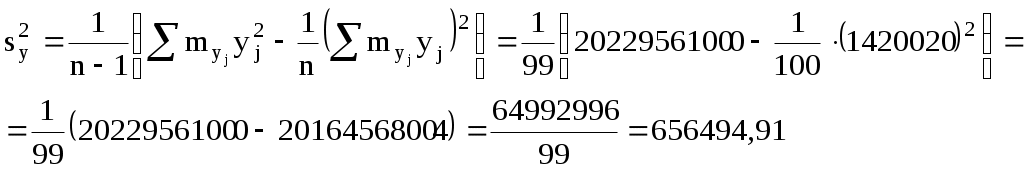
Корреляционный момент вычисляем по формуле


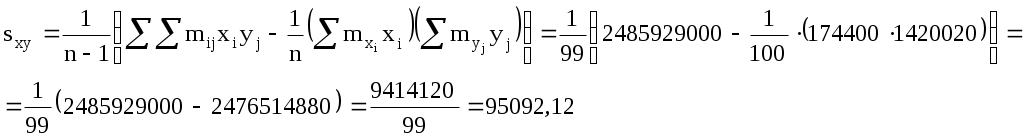
Оценкой теоретической линии регрессии является эмпирическая линия регрессии, уравнение которой имеет вид: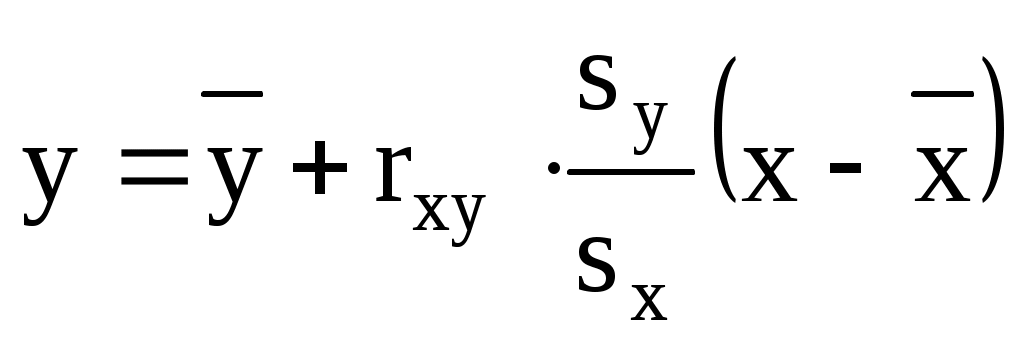

где ;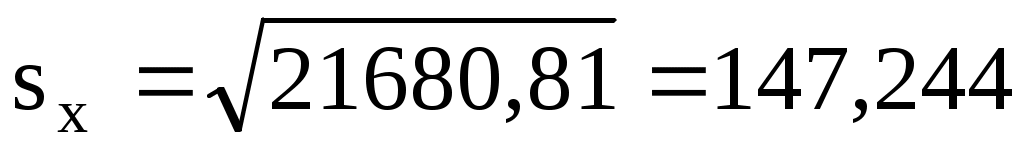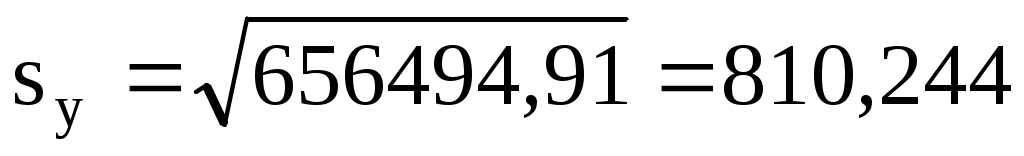



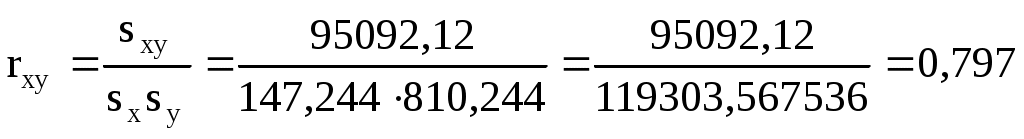
Составляем уравнение эмпирической линии регрессии y на x:

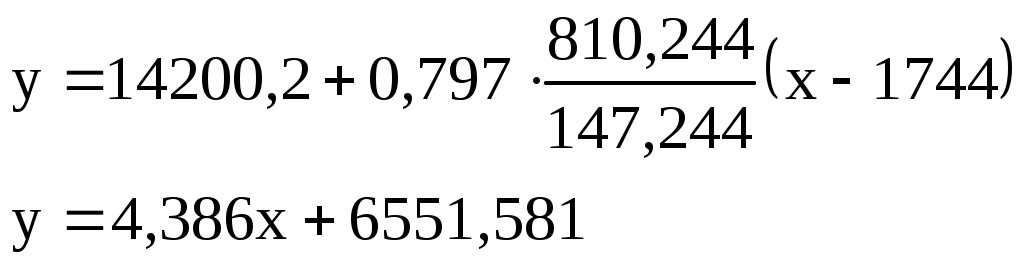
Строим линию регрессии и случайные точки (x_i; y_j)


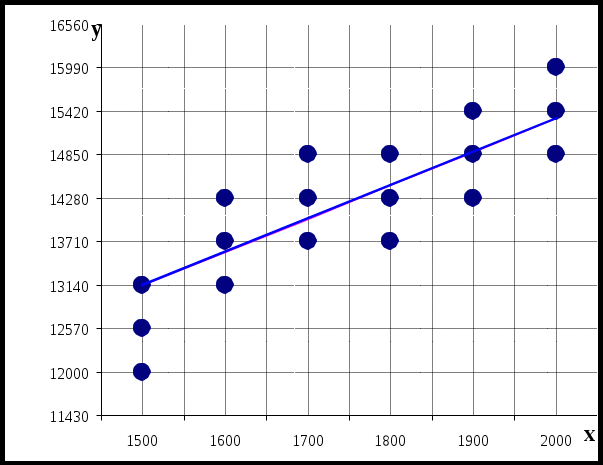
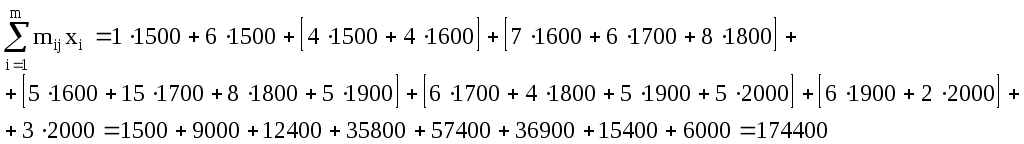
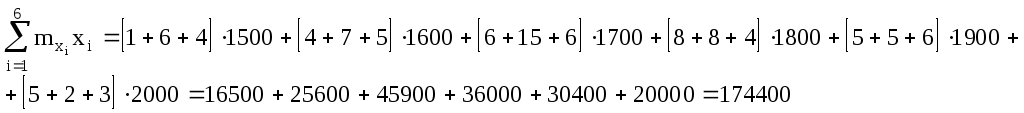
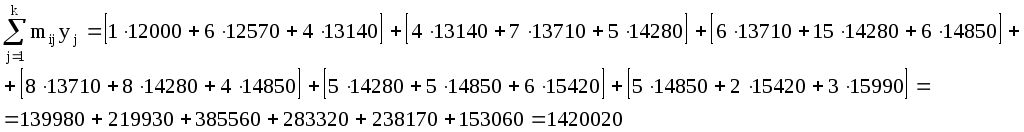
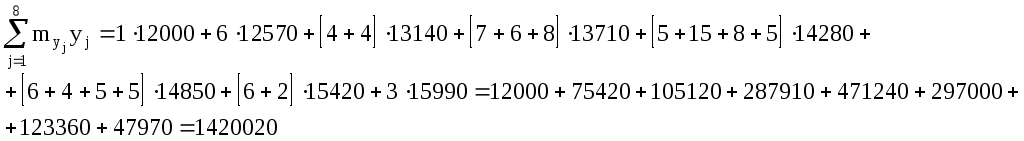
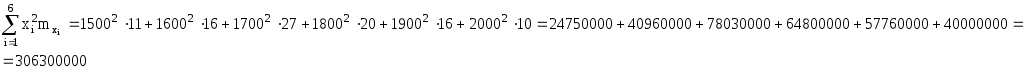
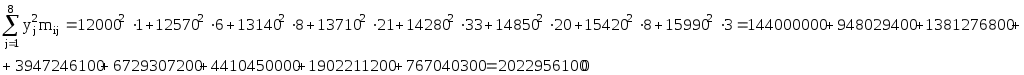
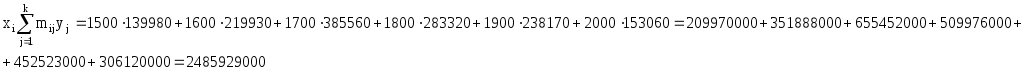
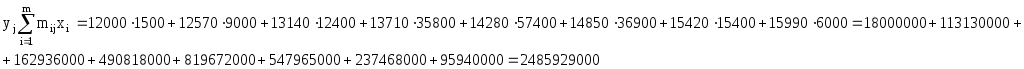
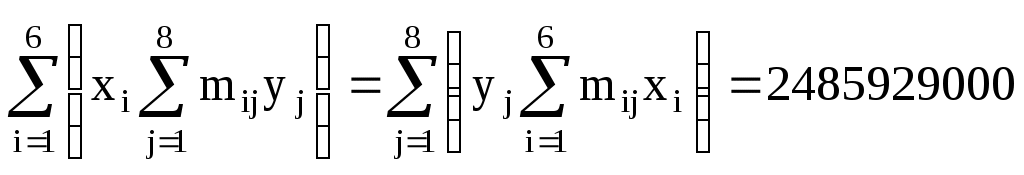
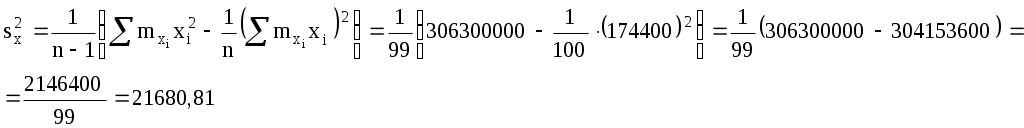
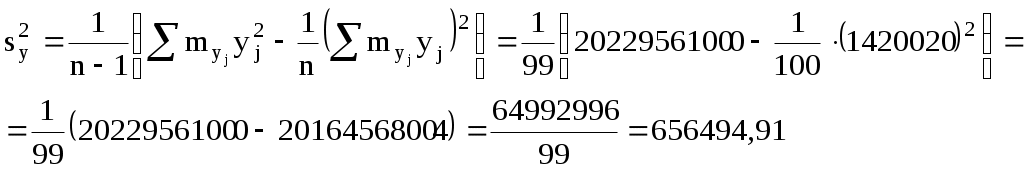
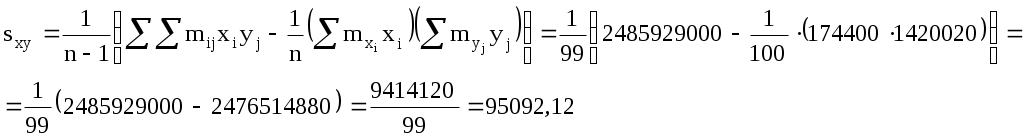
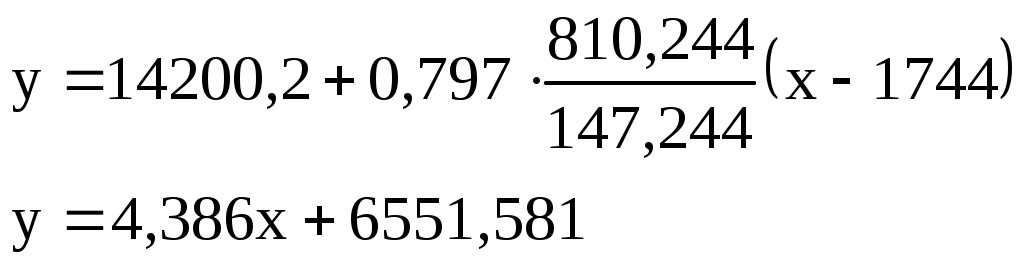
г де - корреляционное поле