2 вар. 2 вариант. А Решение Найдем главный определитель значит, система совместна. Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду Получаем
 Скачать 218.49 Kb. Скачать 218.49 Kb.
|
|
Контрольная работа № 1 1. Даны системы линейных алгебраических уравнений (СЛАУ). Решить их тремя способами: 1) Методом Гаусса, 2) Методом Крамера, 3) Методом обратной матрицы а) 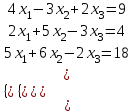 Решение: Найдем главный определитель: 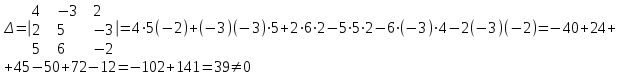 значит, система совместна. Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду: 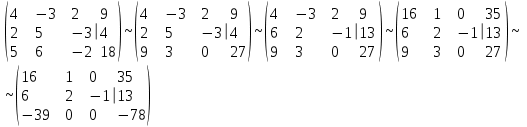 Получаем: 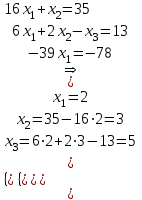 Решение системы: 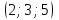 . .Решаем методом Крамера: находим остальные определители путем замены столбцов матрицы столбцом свободных членов: 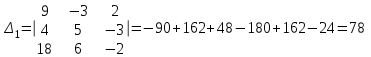 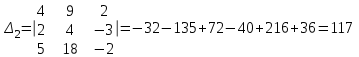 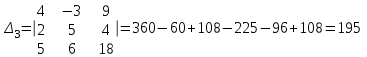 По формулам Крамера получаем: 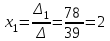 , , 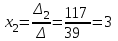 , , 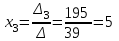 . .Решение системы: 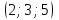 . .Решаем матричным методом: 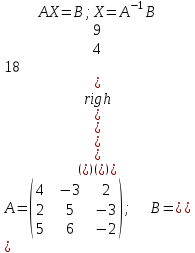 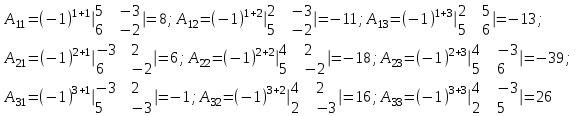 Получаем: 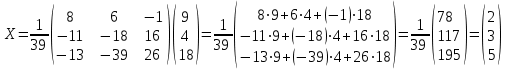 Решение системы: 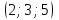 . .б) 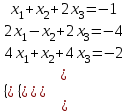 Найдем главный определитель: 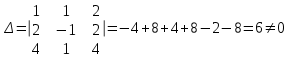 , значит, система совместна. , значит, система совместна.Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду: 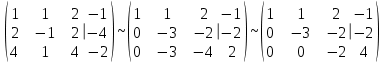 Получаем: 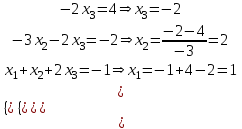 Решение системы: 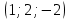 . .Решаем методом Крамера: находим остальные определители путем замены столбцов матрицы столбцом свободных членов: 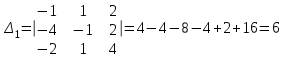 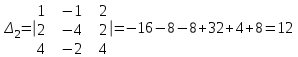 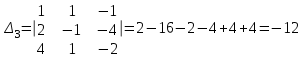 По формулам Крамера получаем: 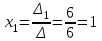 , , 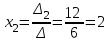 , , 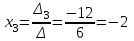 . .Решение системы: 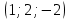 . .Решаем матричным методом: 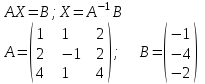 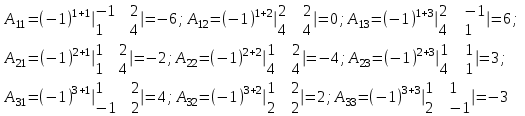 Получаем: 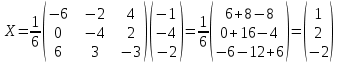 Решение системы: 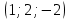 . .2. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей а) 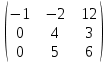 Решение: Составим характеристическое уравнение и найдем собственные числа: 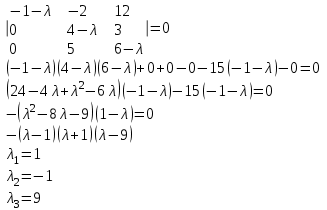 Для каждого числа найдем его вектор: 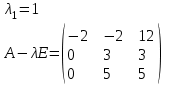 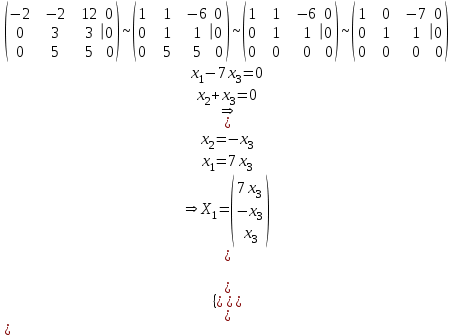 Фундаментальная система: 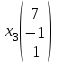 . Пусть . Пусть 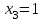 , тогда , тогда 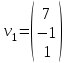 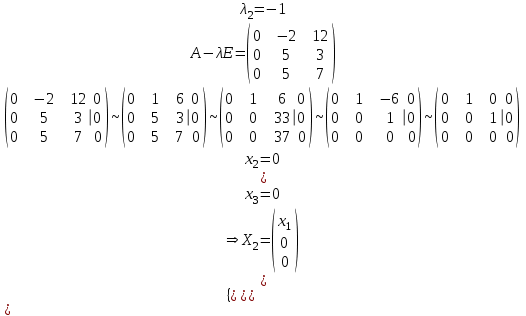 Фундаментальная система: 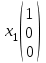 . Пусть . Пусть 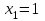 , тогда , тогда 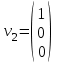 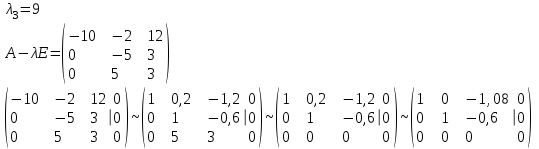 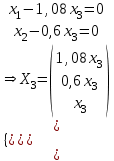 Фундаментальная система: Фундаментальная система: 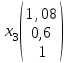 . Пусть . Пусть 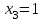 , тогда , тогда 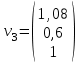 б) 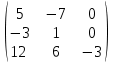 Решение: Составим характеристическое уравнение и найдем собственные числа: 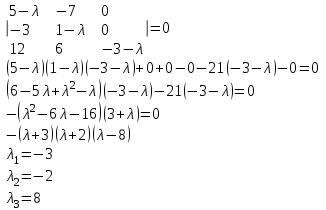 Для каждого числа найдем его вектор: 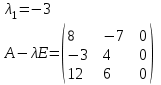 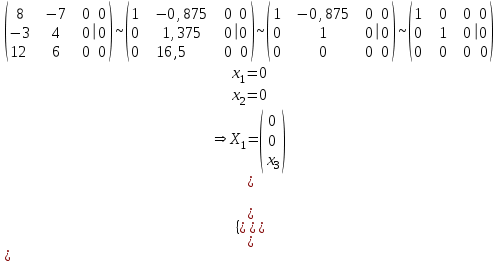 Фундаментальная система: 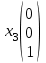 . Пусть . Пусть 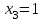 , тогда , тогда 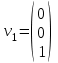 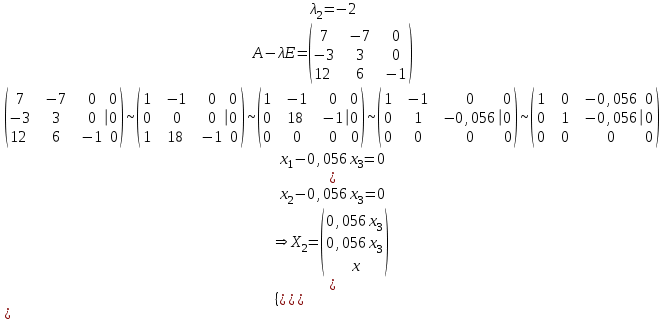 Фундаментальная система: Фундаментальная система: 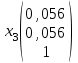 . Пусть . Пусть 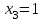 , тогда , тогда 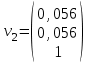 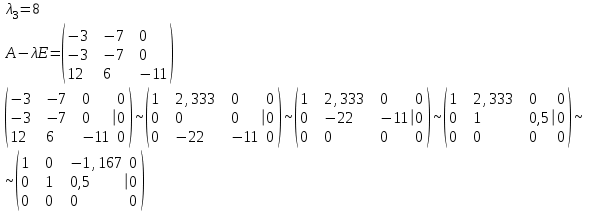 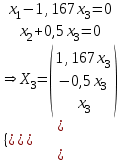 Фундаментальная система: Фундаментальная система: 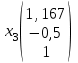 . Пусть . Пусть 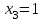 , тогда , тогда 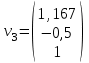 Контрольная работа №2 1. Даны четыре вектора 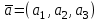 , , 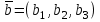 , , 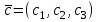 и и 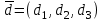 в некотором базисе. Построить новый базис из данных векторов и выразить небазисный вектор в этом базисе. в некотором базисе. Построить новый базис из данных векторов и выразить небазисный вектор в этом базисе.а) 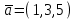 , , 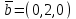 , , 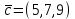 , , 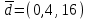 Решение: Используем признак линейной независимости для векторов с числовыми координатами. Вычисляем определитель: 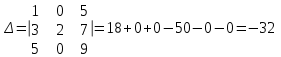 , значит, система векторов линейно независима и образует базис. , значит, система векторов линейно независима и образует базис.Найдем координаты вектора 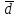 в этом базисе, решая систему: в этом базисе, решая систему:Проведем разложение 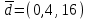 вектора по базису вектора по базису 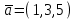 , , 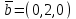 , , 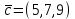 . Запишем разложение вектора . Запишем разложение вектора 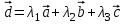 в координатной форме: в координатной форме: 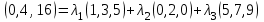 . Получаем систему уравнений: . Получаем систему уравнений: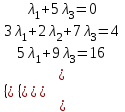 Решаем методом Гаусса: 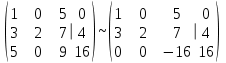 Получаем: 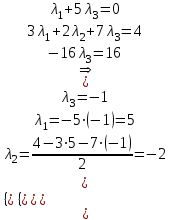 Получили разложение вектора 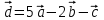 б) 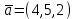 , , 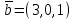 , , 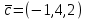 , , 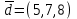 Решение: Используем признак линейной независимости для векторов с числовыми координатами. Вычисляем определитель: 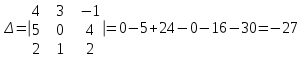 , значит, система векторов линейно независима и образует базис. , значит, система векторов линейно независима и образует базис.Найдем координаты вектора 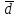 в этом базисе, решая систему: в этом базисе, решая систему:Проведем разложение 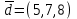 вектора по базису вектора по базису 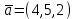 , , 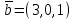 , , 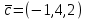 . Запишем разложение вектора . Запишем разложение вектора 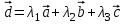 в координатной форме: в координатной форме: 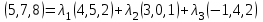 . Получаем систему уравнений: . Получаем систему уравнений: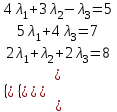 Решаем методом Гаусса: 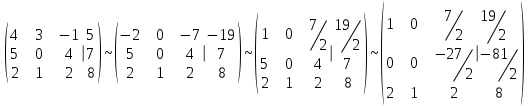 Получаем: 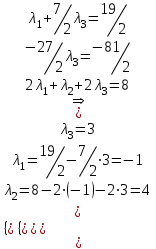 Получили разложение вектора 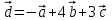 2. Даны координаты вершин пирамиды А1,А2,А3,А4. Найти: 1) длины ребер А1А2, А1А3, А2А3, А3А4; 2) угол между ребрами А1А2, А1А3; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямых А1А2, А1А4; 7) уравнение плоскостей А1А2А3, А1А2А4; 8) угол между плоскостями А1А2А3, А1А2А4; 9) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. а) А1(1,1,2), А2(0,1,6), А3(-1,2,2), А4(1,3,4) Решение: 1) длины ребер А1А2, А1А3, А2А3, А3А4: 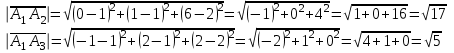 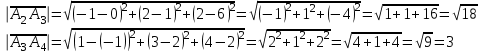 2) угол между ребрами А1А2, А1А3: 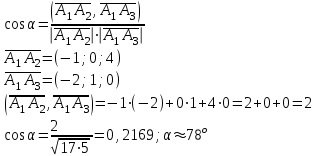 3) угол между ребром А1А4 и гранью А1А2А3: Сначала найдем уравнение грани А1А2А3: 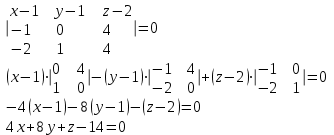 Находим угол: 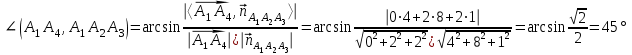 4) площадь грани А1А2А3: 4) площадь грани А1А2А3: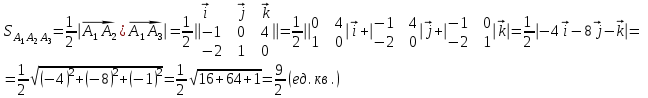 5) объем пирамиды: 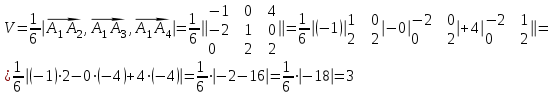 6) уравнение прямых А1А2, А1А4: 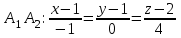 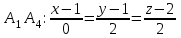 7) уравнение плоскостей А1А2А3, А1А2А4: уравнение грани А1А2А3 мы уже нашли в п. 3: 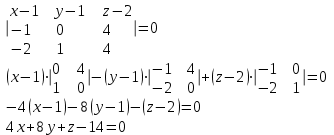 Уравнение грани А1А2А4: 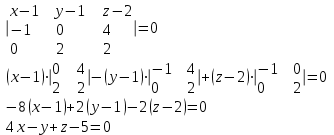 8) угол между плоскостями А1А2А3, А1А2А4: 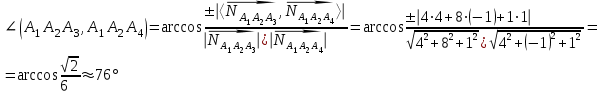 9) уравнение высоты, опущенной из вершины А4 на грань А1А2А3: 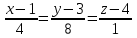 б) А1(-1,-2,1), А2(-2,-2,5), А3(-3,-1,1), А4(-1,0,3) Решение: 1) длины ребер А1А2, А1А3, А2А3, А3А4: 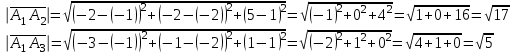 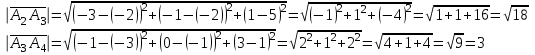 2) угол между ребрами А1А2, А1А3: 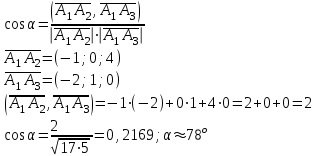 3) угол между ребром А1А4 и гранью А1А2А3: Сначала найдем уравнение грани А1А2А3: 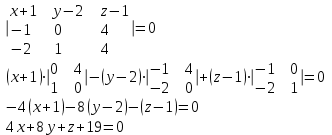 Находим угол: 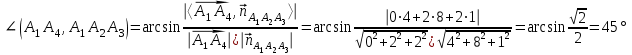 4) площадь грани А1А2А3: 4) площадь грани А1А2А3: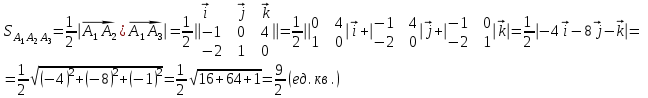 5) объем пирамиды: 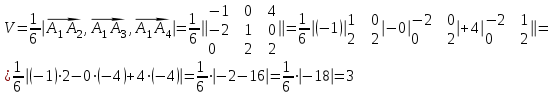 6) уравнение прямых А1А2, А1А4: 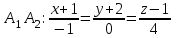 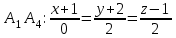 7) уравнение плоскостей А1А2А3, А1А2А4: уравнение грани А1А2А3 мы уже нашли в п. 3: 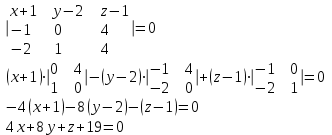 Уравнение грани А1А2А4: 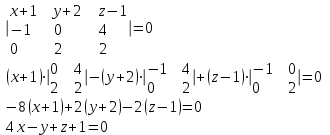 8) угол между плоскостями А1А2А3, А1А2А4: 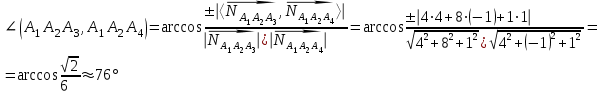 9) уравнение высоты, опущенной из вершины А4 на грань А1А2А3: 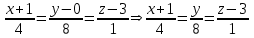 3. Привести к каноническому виду и определить типы кривых второго порядка 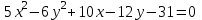 Решение: б) 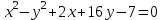 Решение: Приведем уравнение к каноническому виду: 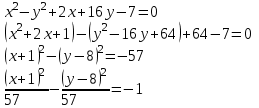 Получили уравнение гиперболы с центром в точке (-1, 8). Строим его: 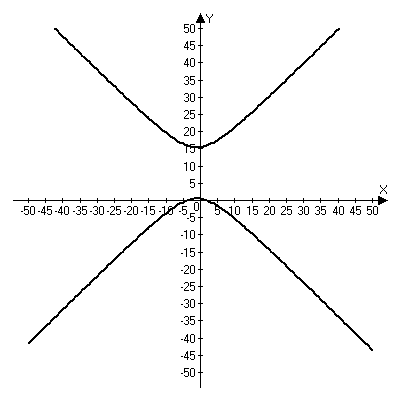 |
