От Антона. А11, а12, а21, а22
 Скачать 135.32 Kb. Скачать 135.32 Kb.
|
              1)Определители второго и третьего порядка 1)Определители второго и третьего порядкаМатрицей второго порядка называется таблица, составленная из 4 элементов: а11, а12, а21, а22 Первое число указывает на номер строки, второе указывает на номер столбца. Чтобы вычислить определитель второго порядка, нужно перемножить элементы, стоящие на главной диагонали, и вычесть произведение элементов, стоящих на побочной диагонали.   Матрицей третьего порядка называется таблица, составленная из 9 элементов. Матрицей третьего порядка называется таблица, составленная из 9 элементов.Матрица, имеющая одинаковое число строк и столбцов, называется квадратной. Число строк в матрице называется порядком матрицы. Определитель третьего порядка можно найти по правилу треугольника, разложением определителя по элементам строки или столбца.   Минором некоторого элемента матрицы - называется определитель, полученный путем вычеркивания строки и столбца, в котором находится этот элемент. Минором некоторого элемента матрицы - называется определитель, полученный путем вычеркивания строки и столбца, в котором находится этот элемент.Алгебраическим дополнением некоторого элемента матрицы – называется его минор, взятый со знаком «плюс», если сумма строки и столбца, в котором находится этот элемент – четная. И со знаком «минус», если сумма строки и столбца, в котором находится элемент – нечетная. 2)Свойства определителей 1 )Определитель не изменится, если его строки заменить на соответствующие столбцы и наоборот. 2) При перестановке 2 строк (столбцов) определитель меняет знак. 3) Если определитель имеет 2 одинаковых строки (столбца), то он равен 0. 4) Если элементы какой-либо строки (столбца) имеют общий множитель, то его можно выносить за знак определителя. 5) Если все элементы некоторой строки (столбца) равны 0, то определитель равен 0. 6) Если элементы какой-либо строки (столбца) представляют собой суммы двух слагаемых, то определитель равен сумме соответствующих определителей. 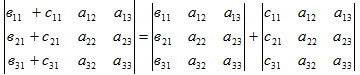 7) Определитель не изменяется, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженной на любое число. 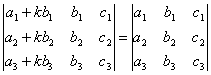 8) Определитель может быть разложен по элементам какой-либо строки. 9) Определитель может быть разложен по элементам какого-либо столбца. 3)Формулы Крамера Правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Правило Крамера: 1)Дана система с тремя неизвестными  2)Находим главный определитель 2)Находим главный определительОбязательным фрагментов оформления является запись: 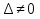 , значит система имеет единственное решение. , значит система имеет единственное решение.3)Находим три определителя: 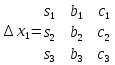 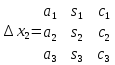 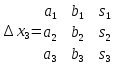 4)Записываем ответ по формулам  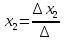 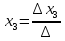 Эти формулы и называются формулами Крамера. 4)Матрицы и действия над ними. Матрица – прямоугольная таблица чисел Aik (i=1,2,3…m) (k=1,2,3…n), содержащая m-строк и n-столбцов. 1)Матрица А, все элементы которой равны 0, называется нулевой матрицей 2)Две матрица А и B одинаковой размерности называются равными, если равны их соответствующие элементы. 3)Матрица А называется квадратной, если m=n (число строк=число столбцов) 4)Квадратная матрица называется единичной, если на ее диагонали стоят единицы, а остальные элементы равны 0. Действия над матрицами: 1)Сложение- чтобы сложить матрицу нужно сложить их соответствующие элементы. 2)Вычитание- аналогично сложению. 3)Умножение матриц на число- произведение числа ƛ на матрицу А называется матрица В, полученная из исходной матрицы умножением на число ƛ всех элементов. B=ƛ*A 4)Произведением матриц Amxn на матрицу Bnxk называется матрица Cmxk такая, что элемент матрицы С, стоящий в i-ой строке и j-ом столбце, т.е элемент Cij, равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В.   5)Обратная матрица Обратная матрица находится по формуле:  Понятие обратной матрицы существует только квадратных матриц. Чтобы найти транспонированную матрицу, надо сначала найти матрицу алгебраических дополнений, затем поменять строки на столбцы. Алгоритм: 1)Находим определитель матрицы Если определитель матрицы равен 0, обратной матрицы не существует. 2)Находим матрицу минором 3)Находим матрицу алгебраических дополнений 4)Транспонируем матрицу алгебраических дополнений (т.е меняем строки на столбцы) 6)Решение систем линейных уравнений матричным способом. Матричный способ – это метод решения системы через обратную матрицу. Обратная матрицасуществует только для квадратных матриц. Если определитель равен 0, то обратной матрицы не существует. Существует два основных метода нахождения обратной матрицы: 1)с помощью алгебраических дополнений 2)с помощью элементарных преобразований Чтобы найти обратную матрицу надо: 1)найти определитель 2)найти все алгебраические дополнения 3)построить матрицу из алгебраических дополнений 4)транспонировать 5)поделить на определитель 7)Метод Гаусса Матрица системы – это матрица, составленная только из коэффициентов при неизвестных. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов. Метод Гаусса – один из наиболее универсальных и эффективных методов решений линейных алгебраических систем. Метод Гаусса заключается в последовательном исключении неизвестных. Процесс решения состоит из двух этапов: На первом этапе (прямой ход): система приводится к ступенчатому (треугольному виду) с помощью элементарных преобразований. Существуют следующие элементарные преобразования 1)Строки матрицы можно переставлять местами 2)Если в матрице появились пропорциональные или одинаковые строки, то следует удалить из матрицы все эти строки кроме одной. 3)Если в матрице в ходе преобразований появилась нулевая строка, то ее следует удалить 4)Строку матрицы можно умножить (разделить) на любое число (отличное от нуля) 5)К строке матрицы можно прибавить другую строку, умноженное на число, отличное от нуля. Всегда меняется строка, к которой прибавляют! Строка, которую прибавляют, не меняется! На втором этапе (обратный ход): идет последовательное определение неизвестных 8)Векторы и линейные операции над ними. Вектор – направленный отрезок. Нулевой вектор – вектор, начало которого совпадает с его концом. Единичный вектор (орта) – длина равна 1. Коллинеарные – лежат на одной прямой или на параллельных прямых. Равные векторы – если они коллинеарны, одинаково направлены и имеют одинаковые длины. Свободные – вектор можно переносить параллельно самому себе, а начало вектора помещать в произвольную точку пространства Компланарные – лежат в одной плоскости или в параллельных плоскостях. ОПЕРАЦИИ: 1)Сложение -по правилу треугольника -по правилу параллелограмма(диагональ – есть сумма векторов) -по правилу многоугольника(n-векторов складываются по этому правилу) 2)Вычитание -по правилу треугольника -по правилу параллелограмма 3)Умножение вектора на число 9)Базис в пространстве R2 и R3 Любая упорядоченная тройка некомпланарных вектора  , называется базисом векторного пространства. А векторы , называется базисом векторного пространства. А векторы  – базисными векторами. – базисными векторами.Любая упорядоченная пара неколлинеарных вектора  на плоскости R2 называется базисом. на плоскости R2 называется базисом.В двумерном случае базис – это произвольная пара неколлинеарных (непараллельных) векторов. В трехмерном случае базис – это любая тройка некомпланарных векторов. Векторы называются компланарными, если существует плоскость, которой они параллельны. Некомпланарные – прямые, не лежащие в одной плоскости. (пример: две скрещивающиеся прямые – некомпланарные) Любой вектор плоскости  единственным образом раскладывается по базису единственным образом раскладывается по базису   Где Где  и и  – действительные числа, и их называют координатами вектора в данном базисе. – действительные числа, и их называют координатами вектора в данном базисе.Выражение  называют разложением вектора называют разложением вектора  по базису по базису  Также его называют линейной комбинацией базисных векторов. Для двух векторов плоскости эквиваленты следующие утверждения: 1)векторы линейно независимы 2)векторы образуют базис 3)векторы не коллинеарны (не параллельны) 4)векторы нельзя выразить через друг друга Следовательно эквивалентны и противоположные утверждения. Для трех векторов пространства эквивалентны следующие утверждения: 1)векторы линейно независимы 2)векторы образуют базис 3)векторы не компланарны 4)векторы нельзя линейно выразить через друг друга Следовательно верны и обратные утверждения. Если определитель не равен 0, значит векторы образуют базис, и являются линейно независимыми. 10)Проекция вектора на ось. Проекция вектора AB на ось l называется число равное длине вектора A1B1, взятое: со знаком «+», если вектор A1B1 сонаправлен оси l со знаком «-», если вектор A1B1 противоположно направлен оси l Теорема: 1)При сложении векторов проекции складываются 2)При умножении вектора на число, его проекция умножается на это число. 3)Проекция вектора а на ось l равна произведению модуля этого вектора на косинус угла между ним и положительным направлением оси l 11)Ортонормированный базис. Декартовы системы координат. На практике часто имеют дело с ортонормированным базисом. Ортонормированный базис – базис, векторы которого попарно ортогональны и длины этих векторов равны 1. Ортонормированный базис связан с декартовой системой координат. Точка О плоскости, которая называется началом системы координат, и ортонормированный базис  ) задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат определяется единственной точкой и двумя единичными ортогональными векторами ) задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат определяется единственной точкой и двумя единичными ортогональными векторами  12)Скалярное произведение. СП. СП – вектора a и b называется число равное произведению длин этих векторов на косинус угла между ними. Свойства: 1) Симметричность. 2)Скалярный квадрат 3)Если , то 4) Если и и 5) 6) Если векторы и заданы своими координатами: 7)Два вектора ортогональны, когда их СП равно 0. 8)С помощью СП находят угол между векторами: 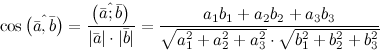 13)Векторное произведение. Векторным произведением – ненулевых векторов и называется вектор , обозначаемый символом или . Вектор c направлен так, что из конца вектора c кратчайший поворот вектора а к вектору b был виден по часовой стрелке. Вектор с определяется следующими условиями: 1)Вектор c перпендикулярен к каждому из векторов a и b 2) Вектор c направлен так, что из конца вектора c кратчайший поворот вектора а к вектору b был виден по часовой стрелке. Обозначение: Общая формула: Свойства векторного произведения: 1) Векторное произведение a на b есть вектор, обратный векторному произведению b на а При перестановке сомножителей векторного произведения нужно ставить перед ним знак минус 2)Если векторы а и b коллинеарны, то их векторное произведение равно 0. 3)Если векторы a и b приведены к общему началу, то модуль векторного произведения 4)Свойство сочетательности по отношению к скалярному множителю 5)Распределительное свойство относительного сложения 14)Смешанное произведение Смешанное произведение – произведение трех векторов, где первые два перемножаются векторно, а их результат умножается скалярно на третий вектор. Смешанное произведение трех векторов равно объему параллепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку. Смешанное произведение векторов является числом! Свойства смешанного произведения: 1)При перестановке любых двух векторов смешанное произведение меняет знак. 2)Если векторы компланарны, то смешанное произведение равно 0. 3)Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю. 4)Если три вектора линейно зависимы (т.е компланарны – лежат в одной плоскости), то их смешанное произведение равно 0. 15)Общее уравнение прямой на плоскости Общее уравнение прямой выглядит следующим образом:  Где коэффициенты  , , 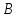 не равны нулю одновременно. не равны нулю одновременно.В зависимости от значений постоянных коэффициентов возможны частные случаи: 1)  – прямая параллельна оси Оx – прямая параллельна оси Оx2)  – прямая параллельна оси Оу – прямая параллельна оси Оу3)  – прямая проходит через начало координат – прямая проходит через начало координат4)В = С = 0 – прямая совпадает с осью Оу 5)A = C = 0 – прямая совпадает с осью Ох 16)Уравнение прямой с угловым коэффициентом. Если в общем уравнении прямой b≠0 , то его можно записать в виде уравнения с угловым коэффициентом: y=kx+b где k=A/B=tgα – угловой коэффициент. α – угол, образованный прямой с положительным направлением оси Ох;  – свободный член, равный ординате точки пересечения прямой с осью Оy – свободный член, равный ординате точки пересечения прямой с осью ОyОпределить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку M1(X1;Y1) c угловым коэффициентом k1, определяется по формуле: 17)Каноническое и параметрические уравнения прямой. Каноническое уравнение получается из параметрических уравнений делением одного уравнения на другой. Каноническое уравнение – уравнение прямой, проходящей через точку 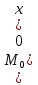 параллельно направляющему вектору параллельно направляющему вектору   Где Где  , ,  , ,  – координаты направляющего вектора – координаты направляющего вектора  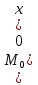 -фиксированная точка, лежащая на прямой -фиксированная точка, лежащая на прямой – произвольная точка на прямой – произвольная точка на прямойВектор  параллелен направляющему вектору параллелен направляющему векторуТаким образом надо построить точу  с координатами с координатами  , чтобы вектор , чтобы вектор  был параллелен направляющему вектору. Поэтому эти координаты векторов из канонического уравнения прямой – пропорциональны. был параллелен направляющему вектору. Поэтому эти координаты векторов из канонического уравнения прямой – пропорциональны.Параметрические уравнения прямой:   Эти уравнения можно выразить в векторном виде.  Где  – фиксированная точка, лежащая на прямой. – фиксированная точка, лежащая на прямой. – произвольная точка, лежащая на прямой. – произвольная точка, лежащая на прямой.18)Уравнение прямой, проходящей через две заданные точки. Пусть даны точки А(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через две заданные точки будет иметь вид:   Если Если  , то прямая проходящая через точки А(x1;y1) и B(x2;y2), параллельна оси ординат. Ее уравнение имеет вид: , то прямая проходящая через точки А(x1;y1) и B(x2;y2), параллельна оси ординат. Ее уравнение имеет вид:  Если  , то уравнение прямой может быть записано в виде , то уравнение прямой может быть записано в виде  19)Угол между прямыми. Условия параллельности и перпендикулярности прямых. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом, то угол между ними определяется по формуле:  Условия параллельности двух прямых: а)равенство угловых коэффициентов б)коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны   Условие перпендикулярности двух прямых: Условие перпендикулярности двух прямых:а)В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности - их угловые коэффициенты обратны по величине и противоположны по знаку: 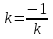 или или  б) Если уравнения прямых заданы в общем виде, то условие их перпендикулярности заключается в выполнении равенства.   20) Уравнение плоскости в отрезках на осях. 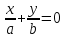 уравнение прямой в отрезках. Эту форму уравнения удобно использовать для построения прямой на чертеже. уравнение прямой в отрезках. Эту форму уравнения удобно использовать для построения прямой на чертеже.a и b величины отрезков, которые прямая отсекает на координатных осях, считая каждый отрезок от начала координат. 21)Расстояние от точки до прямой. Пусть заданы прямая L уравнением  и точка и точка  Требуется найти расстояние от точки  до прямой L до прямой LРасстояние от точки до прямой равно модулю проекции вектора 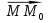 на направление нормального вектора на направление нормального вектора  . Следовательно. . Следовательно.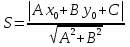 22)Общее уравнение прямой. Уравнение вида  называется общим уравнением прямой (как общее уравнение первой степени). При различных численных значениях A, B, C оно может определять всевозможные прямые без исключения. называется общим уравнением прямой (как общее уравнение первой степени). При различных численных значениях A, B, C оно может определять всевозможные прямые без исключения.Где A, B, C - произвольные постоянные, причем A и B не равны 0 одновременно. При А=0 прямая параллельна оси Ox, при B=0 параллельна оси Оy. При C=0 прямая проходит через начало координат. При y=0 прямая находится на оси Ox. При x=0 прямая находится на оси Oy. Вектор с координатами называется нормальным вектором, он перпендикулярен прямой. Также уравнение может переписать в виде: 23)Угол между плоскостями. Условие параллельности и перпендикулярности. Угол  между двумя плоскостями между двумя плоскостями   равен углу между нормальными векторами  и и     Плоскости Плоскости  и и параллельны тогда и только тогда, когда векторы параллельны тогда и только тогда, когда векторы  и и коллинеарны(параллельны). коллинеарны(параллельны). Плоскости  и и  перпендикулярны тогда и только тогда, когда векторы перпендикулярны тогда и только тогда, когда векторы  и и  ортогональны(перпендикулярны) ортогональны(перпендикулярны) 24)Уравнение плоскости, проходящей через три заданные точки. Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости, проходящей через три данные точки  , ,  , ,  не лежащие на одной прямой. не лежащие на одной прямой.Возьмем на плоскости произвольную точку  Составим векторы    Эти векторы лежат на плоскости, следовательно они компланарны. Используя условие компланарности трех векторов (их смешанное произведение равно 0), получаем  = 0 = 0  Это уравнение плоскости, проходящей через три данные точки. Это уравнение плоскости, проходящей через три данные точки.25)Уравнение плоскости в отрезках на осях  Здесь  величины направленных отрезков, отсекаемых плоскостью на координатных осях величины направленных отрезков, отсекаемых плоскостью на координатных осях  соответственно, т. е. плоскость проходит через три точки: соответственно, т. е. плоскость проходит через три точки:  , ,  , ,  . .26)Расстояние от точки до плоскости Расстояние от точки  до плоскости до плоскости  равно равно  27)Канонические и параметрические уравнения прямой в пространстве Смотри 17 билет, такой же. 28)Уравнения прямой, проходящей через 2 заданные точки.  – уравнения прямой, проходящей через 2 заданные точки M1(x1,y1,z1) и M2(x2,y2,z2) – уравнения прямой, проходящей через 2 заданные точки M1(x1,y1,z1) и M2(x2,y2,z2)При решении задач в качестве направляющего вектора рассматриваемой прямой можно взять вектор  , отсюда , отсюда      29)Угол между прямыми. Условия параллельности и перпендикулярности. Смотри билет 19, такой же. 30)Общее уравнение прямой. Прямая как линия пересечения двух плоскостей. Прямая L в пространстве может быть задана уравнением одного из следующих видов Общее уравнение прямой:  Где коэффициенты Где коэффициенты  , ,  , ,  не пропорциональны коэффициентам не пропорциональны коэффициентам  31)Угол между прямой и плоскостью. Условие принадлежности прямой плоскости. Пусть прямая L задана каноническими уравнениями  а плоскость – общим уравнением  Угол между прямой и плоскостью равен углу между направляющим вектором  (l, m, n) прямой и нормальным вектором (l, m, n) прямой и нормальным вектором  плоскости и вычисляется по формуле: плоскости и вычисляется по формуле:  Условие принадлежности прямой L плоскости P записывается в виде: Условие принадлежности прямой L плоскости P записывается в виде:  ; ;  Где  – координаты точки – координаты точки  , принадлежащей прямой. , принадлежащей прямой.Условия принадлежности прямой плоскости: 1)Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости. 2)Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости. 32)Условие принадлежности прямой плоскости. Смотри билет 24, он такой же. 33)Полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Оp, называемым полярной осью, и единичным вектором  того же направления, что и луч Оp. того же направления, что и луч Оp.Возьмем точку M, не совпадающую с О. Положение точки M определяется двумя числами: -расстоянием r от полюса О -углом  , образованный отрезком ОМ с полярной осью , образованный отрезком ОМ с полярной осьюЧисла r и  называются полярными координатами точки М. Пишут называются полярными координатами точки М. Пишут  При этом r называют полярным радиусом  – полярным углом – полярным угломПолярные координаты точки M выражаются через его декартовы координаты формулами:  Прямоугольные координаты M выражаются через полярные координаты точки следующим: Прямоугольные координаты M выражаются через полярные координаты точки следующим: 34)Преобразование декартовой системы координат. Задача преобразования координат состоит в том, чтобы, зная координаты точки в одной системе координат, найти ее координаты в другой системе. Известны два случая: 1)параллельный перенос осей – меняется начало координат, направления осей остаются неизменными. Уравнения координат x=X+а; Х = х — а; y=Y+b; Y = y — b; X, Y-новая координата x, y-старая координата a, b – координаты нового начала Старая координата равна новой плюс координата нового начала по старой системе. 2)поворот осей – меняются направления осей, начало координат остается неизменным. Уравнения координат x=X cosα-Ysinα y=Xsinα+Y cosα α α – угол между осями 35)Эллипс. Гипербола. Парабола. 1)Эллипс – это множество точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная. Обозначения: F1 F2 – обозначение фокусов 2с – расстояние между фокусами 2а – сумма расстояний от произвольной точки эллипса до фокусов Основное уравнение:  Эллипс – кривая второго порядка Пусть  – произвольная точка эллипса. Отрезки F1M и F2M называют фокальными радиусами точки М. Фокальные радиусы произвольной точки – произвольная точка эллипса. Отрезки F1M и F2M называют фокальными радиусами точки М. Фокальные радиусы произвольной точки  эллипса равны: эллипса равны:   2)Гиперболой – называется множество точек, разность расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная. 2)Гиперболой – называется множество точек, разность расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.Каноническое уравнение гиперболы:  Где Гдеa – вещественная полуось b – мнимая полуось 2с – фокусное расстояние ось Ох – вещественная (фокальная) ось ось Оy – мнимая ось точка О(0;0) – центр гиперболы Гипербола – есть линия второго порядка 3)Параболой – называется множество точек, равноудаленных от некоторой фиксированной точки, называемой фокусом и фиксированной прямой, называемой директрисой. Основное уравнение параболы:  Основные термины, связанные с параболой: ось Ох – ось параболы p – параметр параболы – расстояние от фокуса до директрисы p/2 – фокусное расстояние точка F c координатами (p/2;0) – фокус точка О(0;0) – вершина параболы 36)Эллипсоид. Гиперболоид. Параболоид. Эллипсоид  Числа a, b, c – называются полуосями эллипсоида. Числа a, b, c – называются полуосями эллипсоида.Свойства эллипсоида: 1)Плоскости координат являются плоскостями симметрии 2)Весь эллипсоид расположен в прямоугольном параллепипеде 3)Эллипсоид обладает: -центральной симметрией относительно начала координат -осевой симметрией относительно координатных осей -плоскостной симметрией относительно начала координат 4)В сечении эллипсоида плоскостью, перпендикулярной любой из координатной осей, получается эллипс Гиперболоид Различают однополостные гиперболоиды и двуполостные гиперболоиды. У однополостного гиперболоида каноническое уравнение имеет вид:  У двуполостного гиперболоида каноническое уравнение имеет вид:  Однополостный гиперболоид – поверхность, определяемая каноническим уравнением и имеющая форму бесконечно расширяющейся трубки. Двуполостный гиперболоид – поверхность, имеющая форму выпуклых неограниченных чаш. Свойства однополостного гиперболоида: 1)плоскости координат являются плоскостями симметрии 2)в сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Оz, получается эллипс 3) в сечении однополостного гиперболоида плоскостями, ортогональными осям Ох и Оy, получается гипербола Свойства двуполостного гиперболоида: 1)плоскости координат являются плоскостями симметрии 2)двуполостный гиперболоид – неограниченная поверхность Параболоид Различают эллиптический и гиперболический параболоиды. Эллиптический параболоид – поверхность, имеющая вид выпуклой, бесконечно расширяющейся чаши. Основное каноническое уравнение имеет вид:  Гиперболический параболоид – поверхность, имеющая вид седла. Основное каноническое уравнение имеет вид:  37)Пространство Rn Размерность пространства равна числу линейно независимых векторов В пространстве Rn наибольшее число линейно независимых векторов равно n Любые Пространство R2 В пространстве R2 коллинеарные векторы линейно зависимы, а неколлинеарные векторы линейно независимы. И они образуют базис в пространстве R2. В пространстве R2 наибольшее число линейно независимых векторов равно 2. Любые два линейно независимых вектора образуют базис в пространстве R2. Размерность пространства равна наибольшему числу линейно независимых векторов. Пространство R3 Любые компланарные вектора  линейно зависимы. Любые три некомпланарных вектора линейно зависимы. Любые три некомпланарных вектора  линейно независимы. И они образую базис в пространстве R3. линейно независимы. И они образую базис в пространстве R3.Любой вектор  , принадлежащий пространству , принадлежащий пространству  ( (  ), может быть разложен ), может быть разложен В R3 наибольшее число линейно независимых векторов равно 3. В R3 наибольшее число линейно независимых векторов равно 3.Любые три линейно независимых вектора образую базис в пространстве R3. |
