физика. Альбом по механике. Альбом отчётов к лабораторным работам Механика Молекулярная физика Составители
 Скачать 341.14 Kb.
|
|
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Выполнил(а): студент группы _____________________ ____________________________________ Проверил(а): ________________________ ____________________________________ Дата сдачи отчета:_____________________ Лабораторная работа № 1-3 ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Цель работы: проверка основного закона динамики вращательного движения твердого тела с помощью маятника Обербека. Приборы и принадлежности: лабораторная установка «Маятник Обербека», электронный блок, разновесы. Краткая теория Вращение твердого тела постоянной массы вокруг неподвижной оси подчиняется основному закону динамики вращательного движения: (3.1) В данной формуле: ε - ………………………………………………………………………………….. M - …………………………………………………………………………………. J - …………………………………………………………………………………… 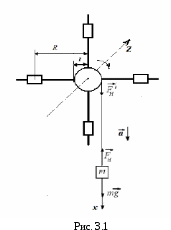 Экспериментальную проверку закона можно провести на приборе, называемом маятником Обербека (Рис. 3.1). Маятник представляет собой крестовину, состоящую из четырех одинаковых стержней и шкива. На стержнях крепятся грузы (цилиндры) одинаковой массы. Маятник может вращаться вокруг горизонтальной оси Z под действием силы натяжения намотанной на шкив нити, к которой подвешен груз m. Данный прибор позволяет менять как момент инерции тела, так и приложенный к нему вращающий момент. Момент инерции маятника можно менять, перемещая цилиндры вдоль стержней или снимая их. Момент силы можно менять, изменяя массу подвешенного груза. Проверку основного закона динамики вращательного движения можно провести в два этапа: 1) при постоянном моменте инерции маятника проверить прямую пропорциональность углового ускорения моменту приложенных сил; 2) при неизменном моменте приложенных сил проверить обратную пропорциональность углового ускорения моменту инерции. Определяемые в работе величины рассчитываются по формулам: Момент силы (3.7) где М - ……………………………………………………………………………... m - …………………………………………………………………………………... d - …………………………………………………………………………………… g - …………………………………………………………………………………… h - …………………………………………………………………………………… t - ……………………………………………………………………………………. Угловое ускорение (3.9) где h - ………………………………………………………………………………. d - …………………………………………………………………………………… t - ……………………………………………………………………………………. Момент инерции (3.10) где J0 - ………………………………………………………………………………. mц - …………………………………………………………………………………. R - …………………………………………………………………………………... Экспериментальная часть 1. Проверка линейной зависимости ε от М при J=const Необходимо при заданных диаметре шкива d и высоте, с которой движется груз h измерить время t опускания груза для каждой задаваемой массы груза m. Измерения провести по три раза. Таблица 3.1
2. Проверка линейной зависимости ε от 1/J при M=const Необходимо оставить на нити груз массой 0,050 кг, надеть на стержни маятника цилиндры общей массой mц и закрепив их на расстоянии R от оси вращения измерить время t опускания груза с той же высоты, что и в первой части работы. Измерение времени провести по три раза для каждого расстояния R. Таблица 3.2
Студент(ка) гр._______________________________________(указать ФИО) Дата выполнения_______________________Преподаватель________________ Обработка результатов измерений 1. Проверка линейной зависимости ε от М при J=const 1.1 Найти среднее значение времени опускания груза для каждого значения массы подвешенного груза m. 1.2 Рассчитать угловое ускорение маятника ε для каждого ε1 = ε2 = ε3 = ε4 = 1.3 Рассчитать момент сил М, вращающих маятник, по формуле (3.7) для каждого значения массы груза, подвешенного к нити. М1 = М2 = М3 = М4 = Результаты расчетов занести в табл. 3.1. 1.4 На листе миллиметровой бумаги форматом не менее, чем А5, построить график зависимости ε от М: по горизонтальной оси откладывать значения М, по вертикальной – ε. С помощью линейки провести из начала координат прямую линию так, чтобы экспериментальные точки распределились равномерно по обе стороны от прямой. 1.5 По котангенсу угла наклона прямой к оси М определить экспериментальное значение момента инерции крестовины маятника 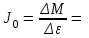 Результат занести в табл. 3.2. 2. Проверка линейной зависимости ε от 1/J при M=const 2.1 Найти среднее значение времени опускания груза для каждого значения расстояния R. 2.2 Рассчитать угловое ускорение маятника ε для каждого ε1 = ε2 = ε3 = ε4 = 2.3 Рассчитать момент инерции J маятника по формуле (3.10) для каждого значения R. J1 = J2 = J3 = J4 = 2.4 Рассчитать величины 1/J, обратные моменту инерции. (1/J)1 = (1/J)2 = (1/J)3 = (1/J)4 = Результаты расчетов занести в табл. 3.2. 2.5 На листе миллиметровой бумаги форматом не менее, чем А5, построить график зависимости ε от (1/J): по горизонтальной оси откладывать значения (1/J), по вертикальной – ε. С помощью линейки провести из начала координат прямую линию так, чтобы экспериментальные точки распределились равномерно по обе стороны от прямой. 2.6 По тангенсу угла наклона прямой к оси (1/J) определить экспериментальное значение момента силы. 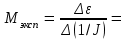 2.7 Рассчитать теоретическое значение момента силы по формуле 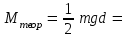 Выводы 1. В данной лабораторной работе проверялся……………………………… …………………………………………………………………………………. 2. В первой части работы проверялось……………………………………….. …………………………………………………………………………………… …………………………………………………………………………………… 2.1 Проведены измерения…………………………………………………….. …………………………………………………………………………………… …………………………………………………………………………………… 2.2 Рассчитаны…………………………………………………………………. …………………………………………………………………………………… 2.3 Построен график зависимости…………………..из которого следует, что………………………………………………………………………………………………………………………………………………………………………… 3. Во второй части работы проверялось……………………………………… …………………………………………………………………………………… …………………………………………………………………………………… 3.1 Проведены измерения……………………………………………………… …………………………………………………………………………………… …………………………………………………………………………………… 3.2 Рассчитаны………………………………………………………………….. …………………………………………………………………………………… 3.3 Построен график зависимости…………………..из которого следует, что………………………………………………………………………………………………………………………………………………………………………… 4. Таким образом, в проведенных опытах основной закон динамики вращательного движения (выполняется, выполняется приблизительно, не выполняется – почему – высказать предположения)…………………………………… …………………………………………………………………………………… …………………………………………………………………………………… Омский государственный технический университет Кафедра физики Отчёт по лабораторной работе №1-4 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ Выполнил(а): студент группы _____________________ ____________________________________ Проверил(а): ________________________ ____________________________________ Дата сдачи отчета:_____________________ Лабораторная работа № 1-4 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ Цель работы: определить момент инерции однородного твердого тела методом крутильных колебаний. Приборы и принадлежности: лабораторная установка «Унифилярный подвес», электронный блок, исследуемое тело, штангенциркуль. Краткая теория Момент инерции тела характеризует…………………………………………. …………………………………………………………………………………… Момент инерции тела зависит………………………………………………… 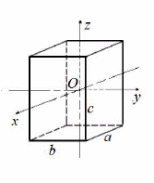……………………………………………………………………………………  Исследуемое тело представляет собой прямоугольный параллелепипед, момент инерции которого относительно осей симметрии может быть вычислен по формулам:Jx = Jy = Jz = (4.3) в которых m - ………………………………………….. a,b,c - ………………………………………. Рис.4.1 ……………………………………………… Экспериментально момент инерции в данной работе определяется методом крутильных колебаний. Исследуемое тело закрепляется в рамке, совершающей крутильные колебания под действием сил упругости. Момент инерции тела рассчитывается по формуле (4.7) В данной формуле J0 - ………………………………………………………………………………. T1 - ……………………………………………………………………………… Tр - ……………………………………………………………………………… Экспериментальная часть Необходимо электронным секундомером измерить время tр десяти (N=10) крутильных колебаний рамки прибора. Затем закрепить в рамке параллелепипед относительно одной из осей симметрии и измерить время десяти (N=10) колебаний рамки с телом. Результаты занести в табл. 4.1. Таблица 4.1
Измерить штангенциркулем размеры параллелепипеда a,b,c . Результаты занести в табл. 4.2 вместе с массой параллелепипеда m. Таблица 4.2
Студент(ка) гр._______________________________________(указать ФИО) Дата выполнения_______________________Преподаватель________________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||