Многочлены. Алгебраическое выражение

• Название: Алгебраическое выражение
• Дата: 06.04.2022
• Размер: 5.82 Mb.
• Имя файла: Многочлены.docx
• Тип: Документы; #447831

Алгебраическое выражение — это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и скобок.

Простейшим алгебраическим выражением является одночлен.

Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения, и при этом не содержит никаких других действий с этими числами и переменными.

Например,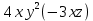

; − одночлены,

а выражения ; − не одночлены.

Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных.

Пример 1

Привести к стандартному виду одночлены: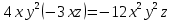

1. 
   
   
2. 
   
   

Два одночлена, приведённых к стандартному виду, называются подобными, если они совпадают или же отличаются только числовым коэффициентом. Сложение и вычитание подобных одночленов называется приведением подобных слагаемых.

Пример 2

Привести подобные члены в выражении:









Многочленом называется сумма одночленов.

Часто бывает полезно преобразовать многочлен так, чтобы он был представлен в виде произведения нескольких сомножителей. Такое тождественное преобразование называется разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих сомножителей. При разложении многочленов на множители применяют три основных приёма: вынесение множителя за скобку, использование формул сокращённого умножения и способ группировки.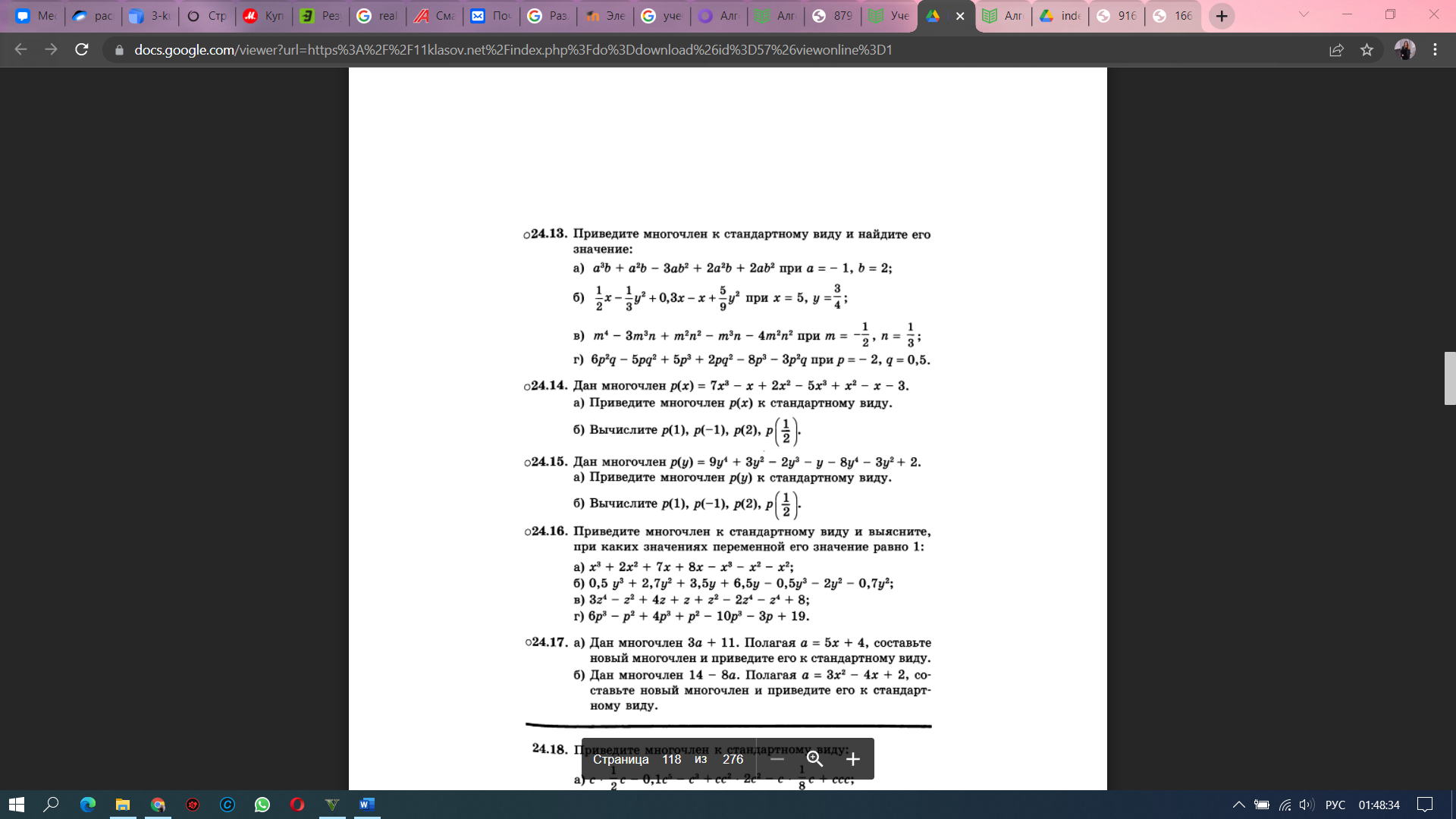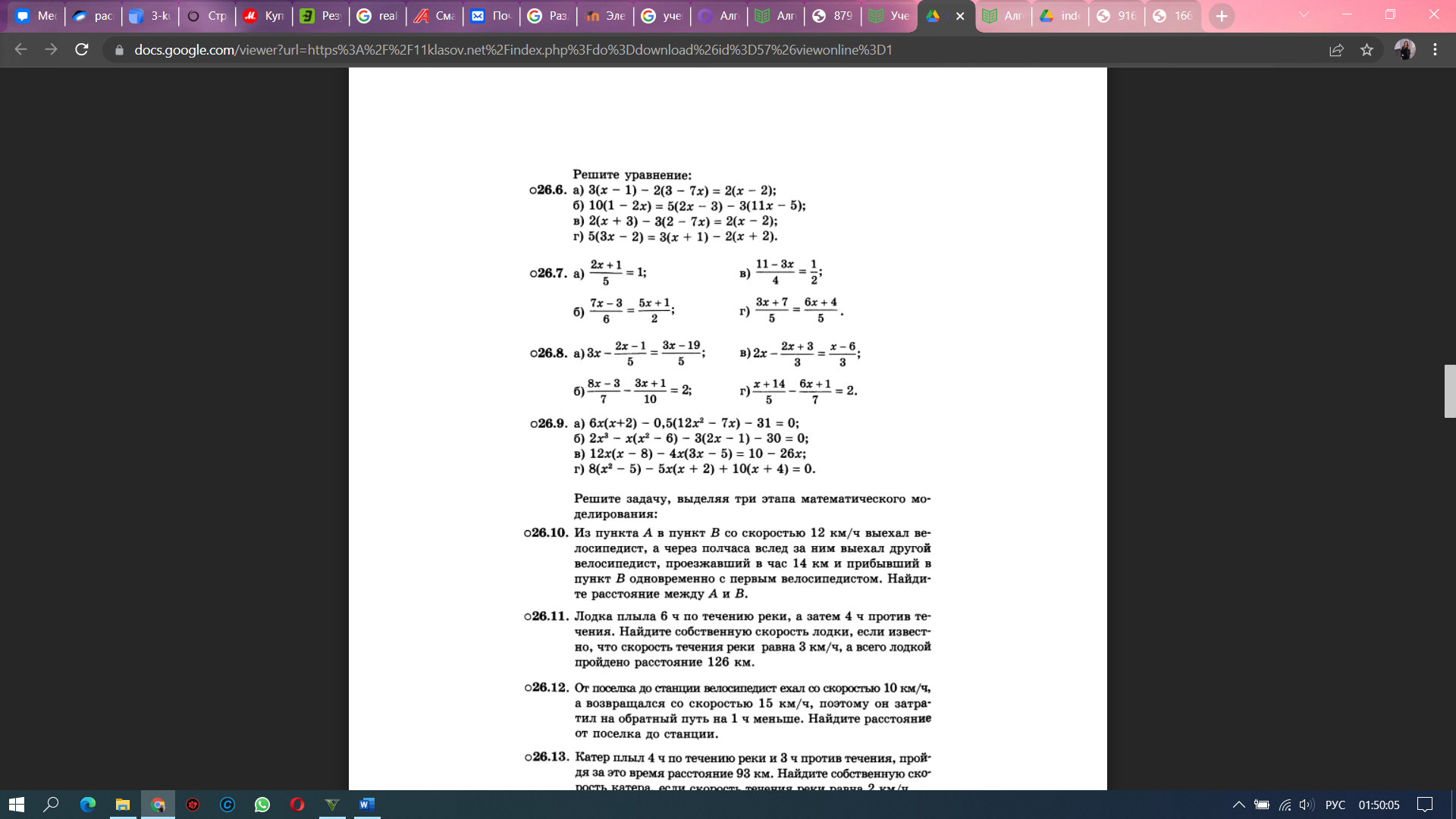







Вынесение множителя за скобку.

Разложение многочлена на множители способом вынесения общего множителя за скобки

Вынести общий множитель за скобки — это значит представить данный многочлен в виде произведения одночлена и многочлена.

Чтобы вынести общий множитель за скобки, нужно:

1) Определить общий множитель у всех членов многочлена.

2) Записать его и открыть скобку.

3) Разделить каждый член многочлена на множитель, записанный перед скобкой.

4) Записать сумму полученных результатов деления каждого члена многочлена на одночлен и закрыть скобку.

Сколько слагаемых было до вынесения общего множителя за скобки, ровно столько же должно остаться в скобках после вынесения.

Пример 1

Разложить многочлен на множители 12y³ – 20y².

Решение

Имеем: 12y3 – 20y2 = 4y2 · 3y – 4y2 · 5 = 4y2(3y – 5). Ответ. 4y2(3y – 5).

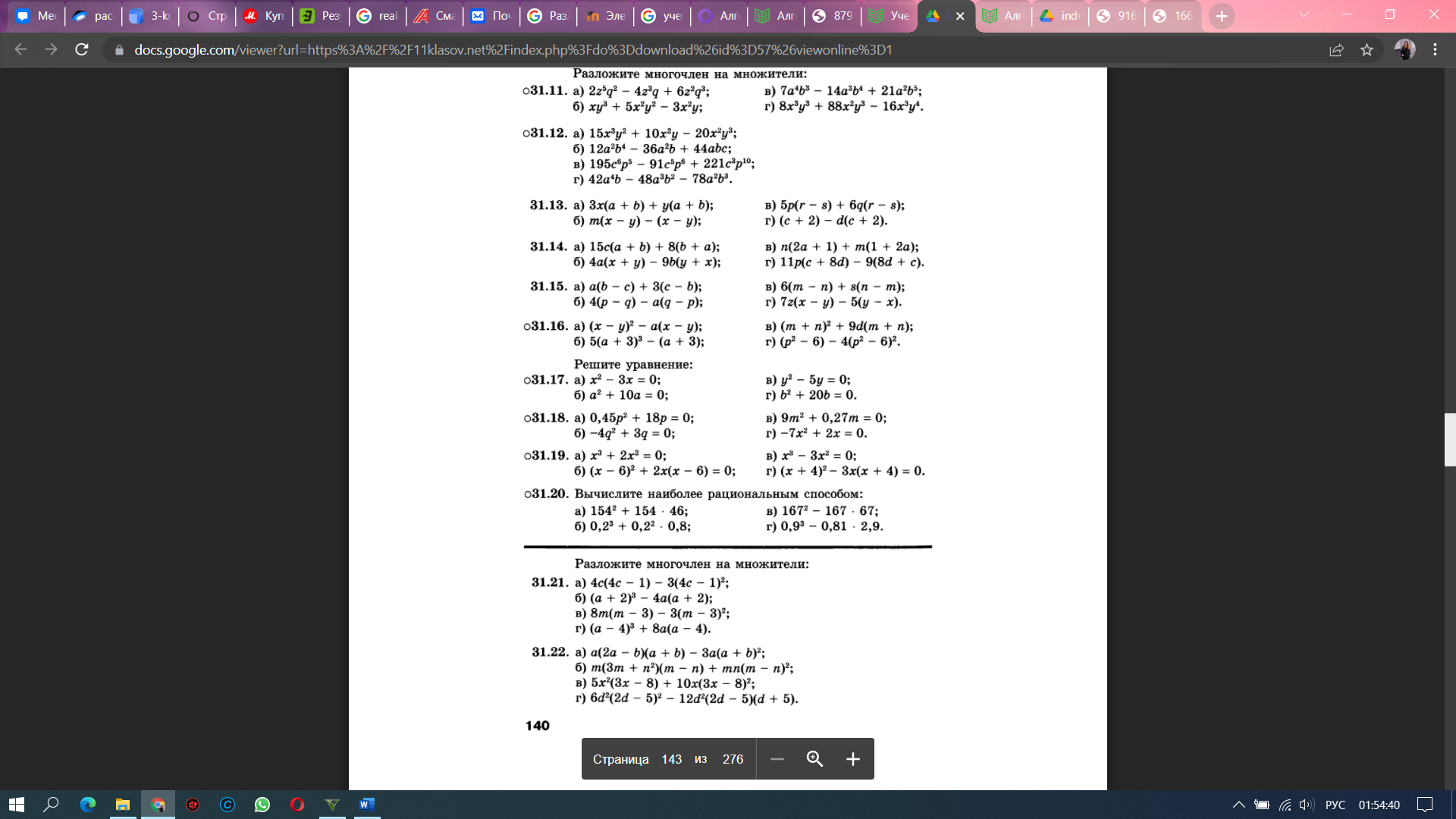Использование формул сокращённого умножения. 



Пример 2

Разложить на множители многочлен x⁴ – 1.

Решение

Имеем: x4 – 1 = (x2)2 – 12 = (x2 – 1)(x2 + 1) = (x2 – 12)(x2 + 1) = (x + 1)(x – 1)(x2 + 1). Ответ. (x + 1)(x – 1)(x2 + 1).

Способ группировки. 

Разложение многочлена на множители способом группировки

Некоторые многочлены можно разбить на группы членов, которые имеют общий множитель, и заключить их в скобки, т. е. сгруппировать.

Чтобы разложить многочлен на множители способом группировки, нужно:

1) Сгруппировать, т. е. заключить в скобки, члены многочлена, которые имеют общий множитель.

2) В каждой группе членов вынести за скобки общие множители.

3) Вынести за скобки общий множитель полученных произведений.

Пример 3

Разложить на множители многочлен x³ – 3x²y – 4xy + 12y².

Решение

Сгруппируем слагаемые следующим образом: x3 – 3x2y – 4xy + 12y2 = (x3 – 3x2y) – (4xy – 12y2). В первой группе вынесем за скобку общий множитель x2, а во второй − 4y. Получаем: (x3 – 3x2y) – (4xy – 12y2) = x2(x – 3y) – 4y(x – 3y). Теперь общий множитель (x – 3y) также можно вынести за скобки: x2(x – 3y) – 4y(x – 3y) = (x – 3y)(x2 – 4y). Ответ. (x – 3y)(x2 – 4y).