Алгоритм Беллмана_Усов_вар26. Алгоритм Беллмана

• Название: Алгоритм Беллмана
• Дата: 12.11.2021
• Размер: 70.93 Kb.
• Имя файла: Алгоритм Беллмана_Усов_вар26.docx
• Тип: Документы; #270379

Алгоритм Беллмана

	1	2	3	4	5	6	7	8	9	10
1	−	1	9	-1	−	−	−	−	−	6
2	5	−	−	−	4	9	2	−	−	−
3	−	−	−	−	7	−	10	−	−	−
4	−	8	−	−	−	−	4	10	6	−
5	3	−	5	7	−	7	−	1	−	−
6	−	1	5	−	−	−	-2	−	1	−
7	−	−	−	9	−	6	−	3	−	−
8	−	−	8	−	−	2	−	−	−	-2
9	3	−	7	−	9	8	9	8	−	−
10	−	5	1	9	−	10	4	−	−	−

1. 
   
   

d^≤2(2) =

d^≤2(3) =

d^≤2(4) =

d^≤2(5) =

d^≤2(6) =

d^≤2(7) =

d^≤2(8) =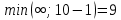

d^≤2(9) =

Заполним 2 строку таблицы.

2. 
   Уменьшились длины путей до вершин 3, 5, 6, 7, 8, 9. Значит, имеет смысл искать более короткие пути до тех вершин графа, в которые входят дуги из перечисленных вершин
   

d^≤3(2) =

d^≤3(3) =

d^≤3(4) =

d^≤3(5) =

d^≤3(6) =

d^≤3(7) =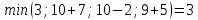

d^≤3(8) =

d^≤3(9) =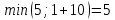

d^≤3(10) =

Заполняем 3 строку таблицы.

3. 
   Уменьшились длины путей до вершин 6, 8. Значит, имеет смысл искать более короткие пути до тех вершин графа, в которые входят дуги из перечисленных вершин
   

d^≤3(2) =

d^≤4(3) =

d^≤4(6) =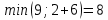

d^≤4(7) =

d^≤4(9) =

d^≤4(10) =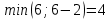

Заполняем 4 строку таблицы.

4. 
   Уменьшились длины путей до вершин 6, 10. Значит, имеет смысл искать более короткие пути до тех вершин графа, в которые входят дуги из перечисленных вершин
   

d^≤3(2) =

d^≤3(3) =

d^≤3(4) =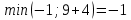

d^≤3(6) =

d^≤3(7) =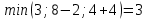

d^≤3(9) =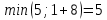

Заполняем 5 строку таблицы

5. 
   Уменьшились длины путей до вершин 3. Значит, имеет смысл искать более короткие пути до тех вершин графа, в которые входят дуги из перечисленных вершин
   

d^≤3(5) =

d^≤3(7) =

Заполняем 6 строку таблицы

	1	2	3	4	5	6	7	8	9	10
1	0	1	9	-1						6
2	0	1	7	-1	5	10	3	9	5	6
3	0	1	7	-1	5	9	3	6	5	6
4	0	1	7	-1	5	8	3	6	5	4
5	0	1	5	-1	5	8	3	6	5	4
6	0	1	5	-1	5	8	3	6	5	4

Длины 6 строки повторяют длины 5 строки. Кратчайшие пути найдены.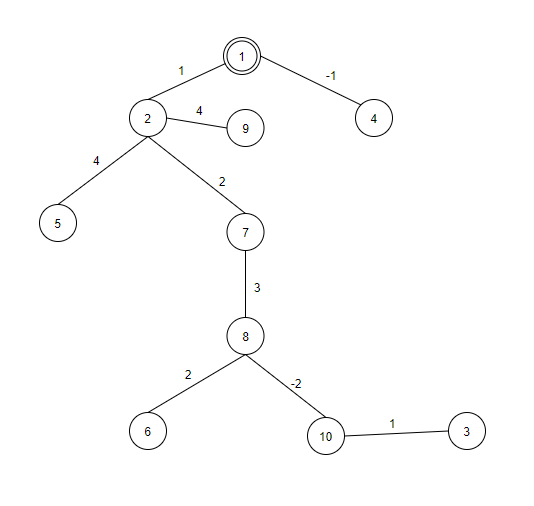