Отчет по лр7. Алгоритмы и программы решения задач вычислительной геометрии
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра радиотехнической электроники отчет по лабораторной работе № 7 по дисциплине «Информационные технологии» Тема: Алгоритмы и программы решения задач вычислительной геометрии
Санкт-Петербург 2022 Цель работы: изучение и программирование алгоритма построения выпуклой оболочки набора точек. Постановка задачи: Заданы: множество S из n точек в двумерном пространстве; алгоритм вычисления полярного угла вектора 1-2; алгоритм построения выпуклой оболочки набора точек (Jarvis) Найти: выпуклый многоугольник, содержащий все точки множества S 1. Реализовать в Программе 1 в Matlab алгоритм вычисления полярного угла вектора 1-2 в виде функции. 2. Протестировать Программу 1 на наборе единичных векторов, начинающихся в начале координат po [0,0] и заканчивающихся в точках sx=[1, -1, -1, 1, 1]; sy=[1, 1, -1, -1, 1]. В полярной системе координат построить график polarplot для единичных векторов 1. Реализовать в Программе 2 в Matlab алгоритм построения выпуклой оболочки набора точек (Jarvis) и вывода результатов (m – количество вершин многоугольника). 2. Оформить отчет, включив в него основную и модифицированную Программы 1 и 2; результаты тестирования Программы 1; исходные и конечные массивы sx, sy; копию построенного в Матлаб графика, подтверждающего полученную выпуклую оболочку Блок-схема Блок-схема алгоритма вычисления полярного угла вектора 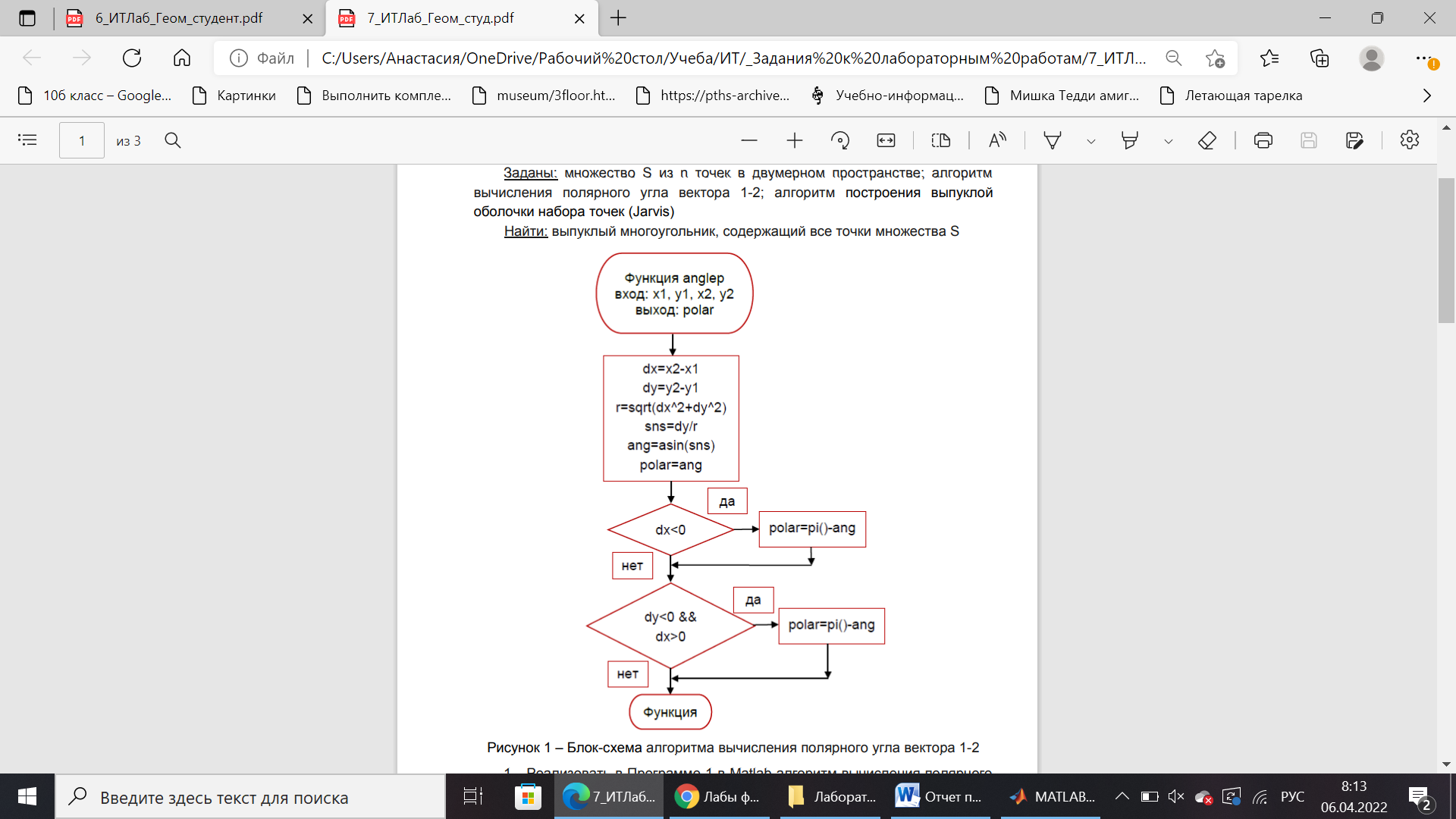 Блок-схема алгоритма построения выпуклой оболочки набора точек (Jarvis) и вывода результатов 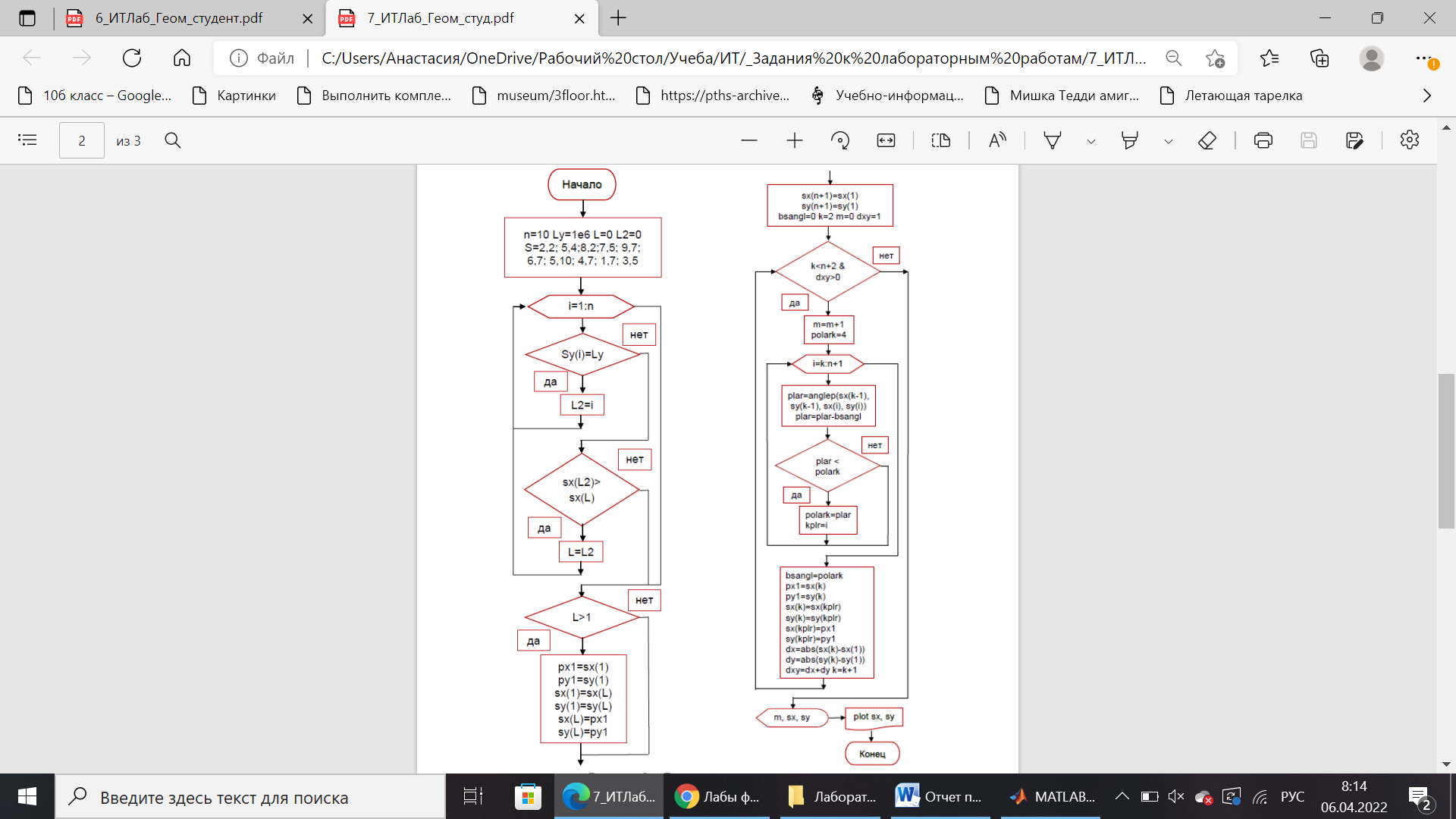 Код программы Код программыПрограмма 1 s1=[1,0,1,0,1,0,1,0,1,0]; sx=[1, -1, -1, 1, 1]; sy=[1, 1, -1, -1, 1]; for i=1:2:10 s(i)=anlep(0,0,sx((i+1)/2),sy((i+1)/2)); s(i+1)=0; disp(s(i)); end polarplot(s,s1) function polar=anlep(x1, y1, x2, y2) dx=x2-x1; dy=y2-y1; r=sqrt(dx^2+dy^2); sns=dy/r; ang=asin(sns); polar=ang; if dx<0 polar=pi()-ang; end if dy<0&&dx>0 polar=2*pi()+ang; end end Листинг программы 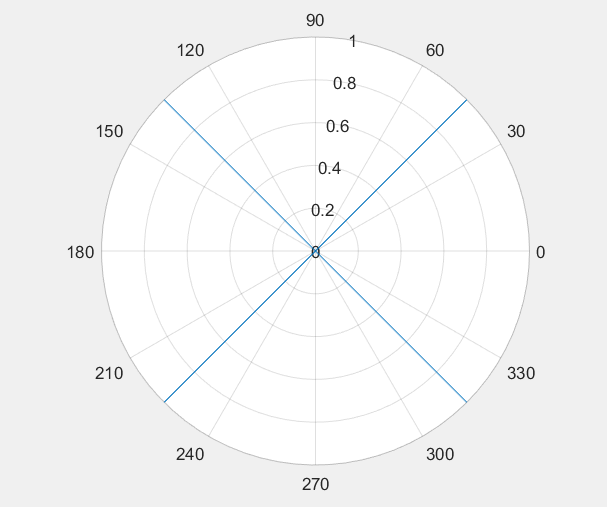 2.3562 0.7854 -0.7854 3.9270 2.3562 Программа 2 sx=[2, 5, 8, 7, 9, 6, 5, 4, 1, 3]; sy=[2, 4 ,2, 5, 7, 7, 10, 7, 7, 5]; for i=1:n %поиск начальной точки if(sy(i) Ly=sy(i);L=i; end if sy(i)==Ly L2=i; elseif sx(L2)>sx(L) L=L2; end end if L>1 %перестановка начальной точки в начало вектора px1 = sx(1); py1 = sy(1);sx(1) = sx(L); sy(1) = sy(L);sx(L) = px1;s(L) = py1; end sx(n+1) = sx(1);sy(n+1) = sy(1); %Добавление начальной точки в конец bsangl = 0;k = 2;m = 0; dxy = 1; while k m = m + 1; polark = 360; r=1e6; for i=k:n+1 plar = anglep(sx(k-1), sy(k-1), sx(i), sy(i), bsangl); r=sqrt((sx(i)-sx(k-1))^2+(sy(i)-sy(k-1))^2); if plar < polark || (plar==polark && r polark = plar; % Уменьшаем величину куда мы можем идти kplr = i; end end bsangl = polark; px1 = sx(k); py1 = sy(k); sx(k) = sx(kplr); sy(k) = sy(kplr); sx(kplr) = px1; sy(kplr) = py1; dx = abs(sx(k) - sx(1)); dy = abs(sy(k) - sy(1)); dxy = dx + dy; k = k + 1; end disp("Количество вершин многоугольника - " + m); disp ("Масив sx") disp(sx); disp ("Масив sy") disp(sy); plot(sx(1:m+1), sy(1:m+1)); function polar = anglep(x1, y1, x2, y2, bsangl) %поиск полярного угла dx=x2-x1; dy=y2-y1;r=sqrt(dx^2+dy^2); sns=dy/r; ang=asin(sns); polar=ang+bsangl; if dx<0 polar = pi - ang; end if dy<=0 && dx>=0 polar = 2*pi + ang; end polar=180*polar/pi(); end Входные данные sx=[2, 5, 8, 7, 9, 6, 5, 4, 1, 3]; sy=[2, 4 ,2, 5, 7, 7, 10, 7, 7, 5]; Листинг результатов 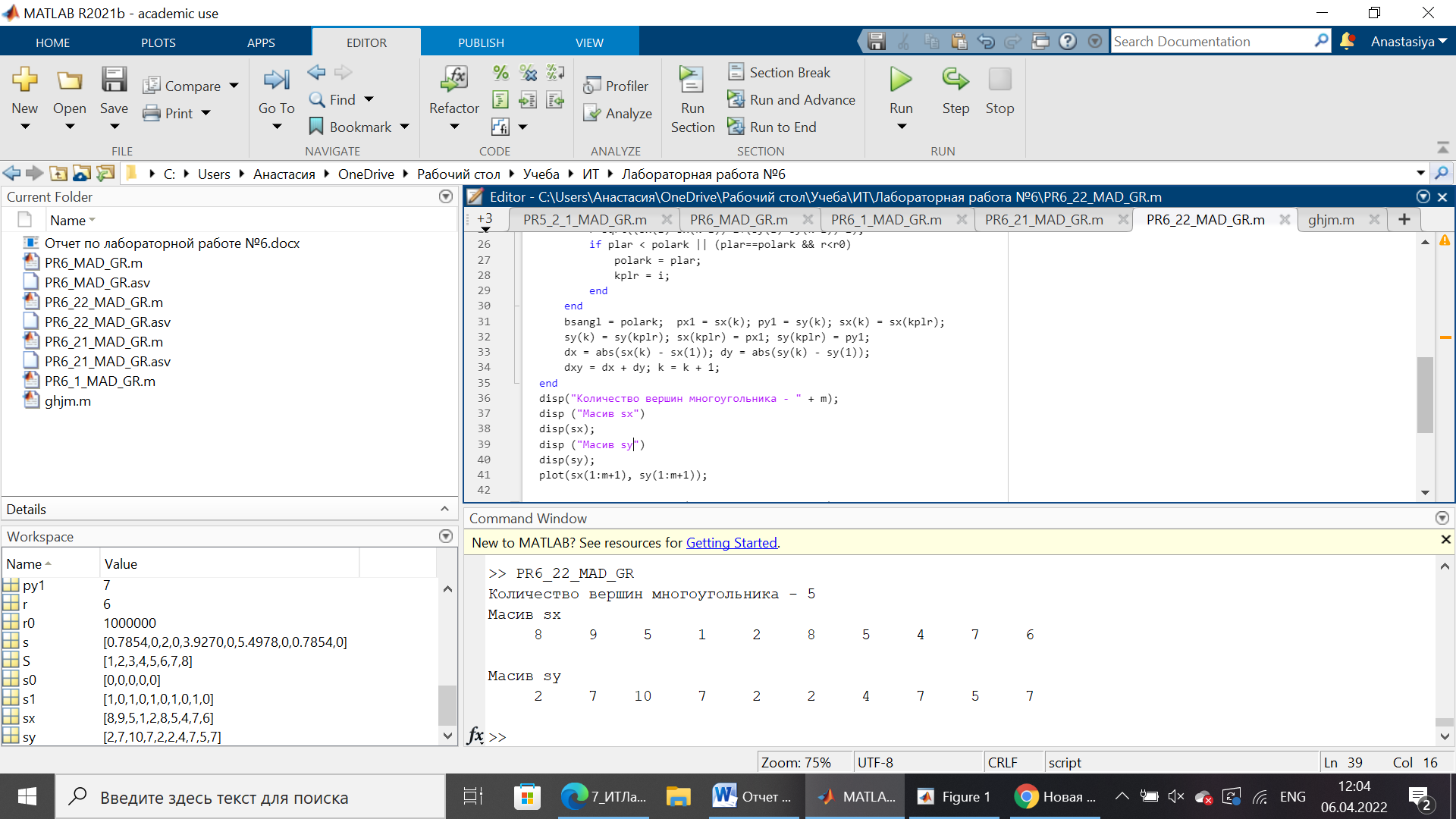 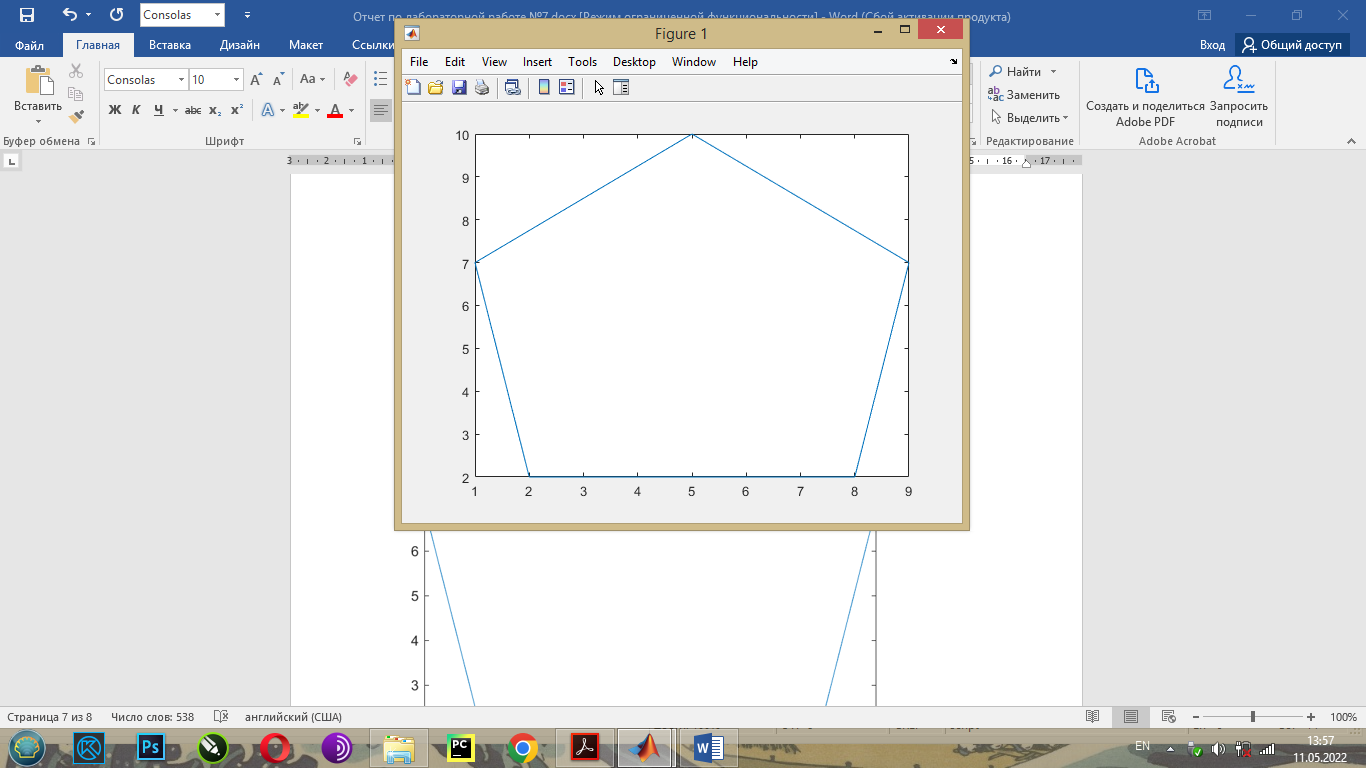 Вывод: При выполнении данной лабораторной работы был изучен и запрограммирован алгоритм построения выпуклой оболочки набора точек. При этом выводились количество вершин многоугольника и сам многоугольник. Также был реализован алгоритм вычисления полярного угла вектора. |
