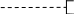1_Лаб_раб_Алгоритмизация. Алгоритмы линейной структуры
 Скачать 114.5 Kb. Скачать 114.5 Kb.
|
Алгоритмы линейной структурыЦель и содержание работы: приобретение навыков составления алгоритмов линейной структуры. Общая постановка задачи 1. Изучите теоретическую часть с основными символами, применяемыми в схемах алгоритмов согласно ГОСТ 19.701 - 90. 2. Изучите алгоритмы линейной структуры на примерах. 3. Разработайте алгоритмы линейных структур и составить их блок-схемы в электронном виде согласно вариантам заданий. Исходные данные вводятся с клавиатуры, результат выводится на экран. 4. Оформите отчет, который должен состоять из: темы, цели лабораторной работы; все блоки по ГОСТ 19.701 – 90 и их значение в виде таблицы (вид таблицы представлен в таблице 1); условия заданий , модели и блок-схемы их алгоритмов по своему варианту. 5. Ответьте на контрольные вопросы и защитите лабораторную работу. Теоретическая частьАлгоритм – конечная последовательность предписаний, однозначно определяющих процесс образования исходящих и промежуточных данных в результате решения задачи. Т.е. алгоритм это четко определенный порядок действий, который необходимо выполнить с целью решения задачи. Применительно к ЭВМ алгоритм определяет вычислительный процесс. Одним из наиболее распространенных способов представлений алгоритмов является графический способ, где алгоритм представляется в виде блок-схем. Построение блок-схем алгоритмов регламентируется ГОСТ 19.701-90 «Единая система программной документации. Схемы алгоритмов программ, данных и систем. Условные обозначения и правила выполнения». Приведем символы, употребляющиеся в схемах программ согласно ГОСТ 19.701-90 (таблица 1). Символ «терминатор» отображает выход во внешнюю среду и вход из внешней среды. Используется для обозначения начала или конца программы или подпрограммы (процедуры или функции). Символ «процесс» отображает обработку данных любого вида, например, выполнение операции или группы операций, приводящее к изменению значения, формы или размещения информации. Чаще всего этим символом обозначают операцию присваивания. Символ «данные» отображает данные, носитель которых не определен. Используется для обозначения операций ввода и вывода данных. Символ «предопределенный процесс» отображает предопределенный процесс, состоящий из одной или нескольких операций, которые определены в другом месте (в подпрограмме или модуле). Таблица 1 – ГОСТ 19.701-90 Схемы алгоритмов, программ, данных и систем
Символ «подготовка» отображает модификацию команды или группы команд. Используется для заголовков циклов с заданным числом повторений (циклов с параметром). Символ «граница цикла» состоит из двух частей, которые отображают начало и конец цикла. Операторы, составляющие цикл, размещаются между символами начала и конца цикла. Условия для инициализации, приращения, завершения и т.д. помещаются внутри символа в начале или в конце в зависимости от расположения операции, проверяющей условие. Обе части символа имеют один и тот же идентификатор. Идентификатор символа должен располагаться слева над символом. Идентификатор определяет символ для использования в справочных целях, например, в листинге программы. Символ «решение» отображает решение или функцию переключательного типа, имеющую один вход и ряд альтернативных выходов, один и только один из которых может быть активизирован после вычисления условий, определенных внутри этого символа. Символ «соединитель» применяется, если схема состоит из нескольких страниц. Символ «комментарий» используют для пояснительных записей в целях объяснения или примечания. Пунктирные линии в символе комментария связаны с соответствующим символом или могут обводить группу символов, текст комментария помещается около ограничивающей фигуры. Символ «линия» отображает поток данных или управления. При необходимости (направления влево или вверх) добавляются стрелки-указатели. Алгоритмы линейной структуры Рассмотрим алгоритмы линейной структуры. Это самый простой вид алгоритмов. В алгоритмах этого типа действия выполняются последовательно одно за другим, в естественном порядке, разветвления отсутствуют. Рассмотрим примеры таких алгоритмов. Пример выполнения работы Пример 1. Вычислить высоты треугольника по заданным сторонам, введенным с клавиатуры. Разработка модели и выбор способа решения. Площадь треугольника, с одной стороны, равна половине произведения основания на высоту, с другой стороны, может быть вычислена по формуле Герона: S = (1/2)aha = (1/2)bhb =(1/2)chc ; где p - полупериметр, p=(a+b+c)/2. Из этих формул можно получить выражения для высот треугольника ha, hb, hc. p:=(a+b+c)/2; t:=2*√(p*(p-a)*(p-b)*(p-c)); ha:=t/a; hb:=t/b; hc:=t/c Схема алгоритма нахождения высот треугольника по заданным сторонам показана рисунке 1. 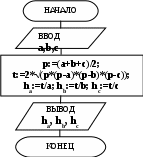 Рисунок 1 – Блок-схема алгоритма нахождения высот треугольника В этом алгоритме вводятся стороны треугольника a, b, c (по свойству массовости алгоритм должен быть пригоден для целого класса однотипных задач, поэтому стороны треугольника не задаются в алгоритме, а вводятся с устройства ввода, причем носитель данных в символе «данные» не определен, это может быть клавиатура, файл и т.п.). Далее вычисляется полупериметр p и удвоенная площадь треугольника t. Далее вычисляются высоты по формуле ha=t/a и аналогичным для b и c. Возникает вопрос, зачем вычислять удвоенную площадь треугольника. Дело в том, что в этом случае умножение на 2 производится один раз при вычислении промежуточной переменной t. Далее t делится на стороны треугольника. Если же вычислять площадь треугольника S, то умножение на два придется выполнить три раза по формулам ha=2S/a, hb=2S/b, hc=2S/c. Введение таких промежуточных переменных сокращает число действий в алгоритме и время работы программы, разработанной по этому алгоритму. По этой причине, прежде чем разрабатывать алгоритм, следует внимательно рассмотреть встречающиеся в формулах выражения и отметить повторяющиеся выражения (в приведенном примере это 2S). Для повторяющихся выражений целесообразно ввести промежуточную переменную, в рассматриваемом случае это t=2S. Далее в алгоритме производится вывод полученных результатов (высот треугольника) и алгоритм завершает работу. Для вывода используется символ «данные», носитель данных не определен. Это может быть монитор, принтер и т.п. В алгоритме нет разветвлений и циклов, все действия производятся в естественном порядке, следовательно, это алгоритм линейной структуры. Пример 2. Вычислить длину окружности, площадь круга и объем шара, имеющих радиус R (R- любое целое число, введенное с клавиатуры). Разработка модели и выбор способа решения. Для вычислений используем формулы L=2πR, S=πR2, V=πR3×4/3= RS× 4/3. Блок-схема решения задачи представлена на рисунке 2, из которого видно, что алгоритм имеет линейную структуру. 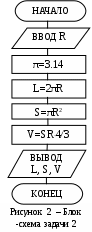 Обратите внимание, что при вычислении V используется значение S, позволяющее упростить вычисления и не использовать операцию возведения в степень. Блоки 3,4,5,6 можно изображать в отдельных блоках (рисунок 2) или в одном, как на рисунке 1. Список индивидуальных заданий Разработайте алгоритмы для четырех заданий, указанных в соответствии с вариантом, из таблиц 2 и 3. Таблица 2 – Варианты и задания
Таблица 3 – Условия заданий
Контрольные вопросы к защите 1. Дайте понятие алгоритма. 2. Перечислите свойства алгоритмов. 3. Какие существуют способы описания алгоритмов. 4. Какие алгоритмы являются линейными? 5. Какие блоки используются в линейных алгоритмах? 6. Назначение основных блоков, используемых для изображения алгоритмов в блок-схемах? |