Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 21 из 67

ЗАДАНИЕ 5. Функции пользователя

Первыйуровеньсложности

Составить программу из задания3 (второй уровень сложности), в которой для каждого x, изменяющегося от a до b с шагом h, вычисление значений Y(x) и S(x) оформить в виде функций пользователя.

В основной функции реализовать следующие действия:

• 
  ввод исходных значений a, b, hи n;
  
• 
  обращение к функциям расчета Y(x) и S(x);
  
• 
  вывод результатов в виде таблицы.
  

Если в задании используется значение факториала, его расчет также оформить функцией.

Второйуровеньсложности

Решить поставленную задачу с использованием рекурсивной и обычной функций. Сравнить полученные результаты.

1. 
   Для заданного целого десятичного числа Nполучить его представление в p-ичной системе счисления (p < 10).
   
2. 
   В упорядоченном массиве целых чисел a _i(i=1, ..., n) найти номер находящегося в массиве элемента c, используя метод двоичного поиска.
   
3. 
   Найти наибольший общий делитель чисел Mи N, используя теорему Эйлера: если Mделится на N,то НОД(N, M) = N,иначе НОД(N, M) = (MmodN, N).
   
4. 
   Числа Фибоначчи определяются следующим образом: Fb(0) = 0;
   

Fb(1) = 1; Fb(n) = Fb(n-1) + Fb(n-2). Определить Fb(n).

5. 
   Найти значение функции Аккермана A(m, n), которая определяется для всех неотрицательных целых аргументов m и n следующим образом:
   

A(0, n) = n+ 1;

A(m, 0) = A(m-1, 1); при m> 0;

A(m, n) = A(m-1, A(m, n-1)); приm> 0 и n> 0.

6. 
   Найти методом деления отрезка пополам минимум функции f(x) =
   

= 7sin²(x) на отрезке [2, 6] с заданной точностью ε (например 0.01).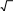

7. 
   Вычислить значение x= a, используя рекуррентную формулу x_n=
   

1 ^� a^�

= ₂ ^�x,_n−в₁ +качест^�ве начального значения использовать x₀ = 0,5(1 + a).

□ ^xn−1 �

8. 
   Найти максимальный элемент в массиве a_i(i=1, …, n), используя
   

очевидное соотношение max(a₁, …, a_n) = max[max(a₁, …, a_n-1), a_n].

9. 
   Вычислить значение y(n) =
   

1+K2 +

n+.

10. 
    Найти максимальный элемент в массиве a _i(i=1, …, n), используя соотношение (деления пополам) max(a ₁,…, a_n) = max[max(a₁,…, a_n/2), max(a_n/2+1, …, a_n)].
    

11. 
    Вычислить значение y(n) =
    

n+

(n

1 _.

1

1) +− ¹

(n2) +− ¹

L

L+ ¹

1+ ¹

2

12. 
    Вычислить произведение четного количестваn(n≥2)
    

�^{2 2}� �^{4 4}� �^{6 6}

сомножителей следующего вида y=_� � _{� �} � _{� �} � … .

_�1 3_{� �}3 5_{� �}5 7

13. 
    Вычислить y= xⁿпо следующему правилу: y= ( x^n/2 )², если n
    

четное и y= x� ⁿy^-1, если nнечетное.

14. 
    Вычислить значение
    

15. 
    Вычислить y(n) =
    

n!


=

k

C
_n(значение 0! = 1).

k!(n− k)!

¹ , nзадает число ступеней.

1 + ¹

1 + ¹

1+ ¹

L