Алгоритмизации
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
ЗАДАНИЕ 1. Составление линейных алгоритмовПервыйуровеньсложностиСоставить программу для расчета двух значенийz 1 и z2, результаты которых должны совпадать [32]. Ввод исходных данных можно задавать при декларации или вводить с клавиатуры. Игнорировать возможность деления на ноль. Значение π = 3,1415926. 1. z2sin 2 (3 2 ) cos2 (5 2 ),π=−z1 1 s+in �5 8α � 1 2 α 4 −= 4 π� π− �. �2 � z cos sin cos 3 sin 3 , z 2 cos α=�αsi+n �π 2=α+� 1 z = sin 2α sin 5α sin 3α , z 2 2 sin α=. α�+α+α �. 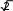 �4 � �4 �1 cos 1 −+2αsin 2 2α 2 z cos 2 �3 π=− β � co−s 2 �11 β� = β 4 1 � � �8 � � +π �, z2 �8 4 � sin . 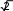 2 2 2 25. z1 1 1 sin 2 2 4 cos 2 , z2 cos 2 cos 4−α=+.α=α+α z cos cos 2 cos 6 cos 7 , z=α4+cαos α c=os 5 α �cos 4α . 1 2 + 2 2 z cos 2 �3 π=− α � co−s 2 �11 α � = sin α . 1 � � � +π �, z2 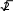 �8 4 � �8 4 � 2 2 �8 4 � �8 4 � 2 2z1 =cos 4 x sin 2 y sin 2 2x1 , 4 z2 +sin( y=−+x) �s+in( y− x) . z1 (cos α=− cos β) 2 − (sin sin ) 2 , zα2 − −=4βsin 2 α − β 2 cos( □ β)+.α � sin �π 3α+� � 5 3 z = �2� , z ctg� α+�π= 1 1 − sin(3α − π) 1 − 2 sin 2 α 2 � �. �4 2 � 1 − tgα z1 = 1 , sin 2α+ z2 =1 . tgα+ z= sin 4α □ cos 2α , z ctg�3 π=− α �. 1 1 cos 4α+1 cos 2α+ 2 � � �2 � z = sin α cos(2 β α) , z= 1 + sin 2 β . 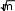 1 cos α − sin(2 β − α) 2 cos 2 β 1 cos α − sin(2 β − α) 2 cos 2 β1 z= (m−1) – (n− 1) − 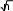 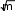 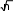 , z2 = m. , z2 = m. 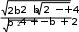  1 1z1 = , z2 = . ВторойуровеньсложностиСоставить программу для расчета заданных выражений. Вводить исходные данные с клавиатуры. Обязательно проверять исключительные ситуации. Значение π = 3,1415926. □ π� �. 2 cos �x− � 2 t= �6��1 + z� � � 0,5 + sin 2 y� 3 − z2 / 5 � 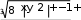 При x= 14.26, y= –1.22, z= 3.5×10-2, результат t= 0.564849. При x= 14.26, y= –1.22, z= 3.5×10-2, результат t= 0.564849.u= x2 + y2 + 2 ex−y(tg2 z+−1)x . При x= –4.5, y= 0.75×10-4, z= 0.845×102, результат u= –55.6848. 1 + sin 2 (x+ y) y 2 � 1 �
v= x+ cos �arctgz�. □ � При x= 3.74×10-2, y= –0.825, z= 0.16×102, результат v= 1.0553. (1+2 sin 2 y)� z2 z3 z4 � w cos x cos y �1 +−z=+ □ 2 + + �. 3 4 � При x= 0.4×104, y= –0.875, z= –0.475×10-3, результат w= 1.9873. 5. =αln�y− � y� − � 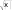 x�+ x�+ □ 2 � sin 2 arctg(z). При x= –15.246, y= 4.642×10-2, z= 20.001×102, результат α = –182.036.  6. 120(3 6. 120(3x=βxy+2 ) �(+arcsin z− x− y) . При x= 16.55×10-3, y= –2.75, z= 0.15, результат β = –38.902. 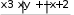 1 17. 5arctg(x) −= 4 x . yz+−x2  При x= 0.1722, y= 6.33, z= 3.25×10-4, результатγ = –172.025. При x= 0.1722, y= 6.33, z= 3.25×10-4, результатγ = –172.025. 8. =� 8. =�ex− y x − y x+ y arctg(x) + arctg(z) При x= –2.235×10-2, y= 2.23, z= 15.221, результат � = 39.374. 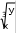 ycos y− ycos y−z (y− x) 9. x x (y−+x−) 1 (y−+x)2 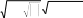 При x= 1.825×102, y= 18.225, z= –3.298×10-2, результат ψ = 1.2131. При x= 1.825×102, y= 18.225, z= –3.298×10-2, результат ψ = 1.2131.10. a= 2−x x+ 4 y3 ex−1/ sin z. При x= 3.981×10-2, y= –1.625×103, z= 0.512, результат a= 1.26185. □ sin 2 z� � 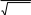 xy�−1 +� xy�−1 +� � 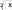 x+ y� x+ y�b= y + cos3 (y)��. ex− y+ x 2 При x= 6.251, y= 0.827, z= 25.001, результат b= 0.7121. y� π� с 2(yx ) (=3 x)y □ arctgz− � 6 −+ � �. x+ 1 y2 + 1 . При x= 3.251, y= 0.325, z= 0.466×10-4, результат c= 4.025.  4 y3 4 y3x−+1 f= x y(sin 2 z+−tgz) При x= 17.421, y= 10.365×10-3, z= 0.828×105, результат f= 0.33056. g= yx+1 x+ y 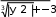 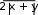 + 2 + 2(x+ 1)−1 / sin z . При x= 12.3×10-1, y= 15.4, z= 0.252×103, результат g= 82.8257. h = xy1 + ey−1+ (  1 1 y− x2  ) 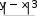 y x+−+ − . y x+−+ − . 2 3 При x= 2.444, y= 0.869×10-2, z= –0.13×103, результат h= –0.49871. | ||||
