ТЭЦ. тэц. Анализ электрического состояния разветвленной электрической цепи синусоидального тока
 Скачать 105.52 Kb. Скачать 105.52 Kb.
|
|
Анализ электрического состояния разветвленной электрической цепи синусоидального тока. План: Анализ физических процессов, имеющих место в магнитной цепи с переменной магнитодвижущей силой. Форма кривой тока идиализированной с магнитной переменной магнитодвижущей силы. Векторная диаграмма и схема замещения. Векторная диаграмма и схема замещения реальной магнитной цепи. 1 Анализ физических процессов, имеющих место в магнитной цепи с переменной магнитодвижущей силой. В этих цепях используется индукционное устройство магнитного поля, в основе которого лежит закон электромагнитной индукции Фарадея – Максвелла. Согласно этого закона в неподвижном контуре, помещенном в изменяющемся во времени магнитное поле, наводится ЭДС, равная: 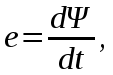 (5.1) (5.1)где ψ = wф – потокосцепление или: 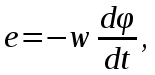 (5.2) (5.2)где w – число витков контура. В толще самого магнитопровода также наводится ЭДС , под давлением которого возникают токи, называемые вихревыми токами. Вихревые токи вызывают дополнительный нагрев сердечника. При анализе физических процессов, имеющих место в магнитной цепи с переменой МДС, результирующее потокосцепление рассматривают состоящим как бы из двух: рабочего потокосцепления ψр, магнитные силовые линии которого замыкаются по магнитопроводу и потокосцепления рассеяния ψs, магнитные силовые линии которого замыкаются по неферромагнитной среде вокруг обмотки. Каждый из этих потокосцеплений наводит ЭДС в намагничивающей обмотки возбуждения: 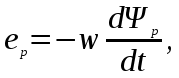 (5.3) (5.3)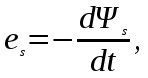 (5.4) (5.4)Далее записывают уравнение напряжений для намагничивающей обмотки возбуждения: U = (-ep) + (-es) + Rобм i, (5.5) где Rобм – активное сопротивление намагничивающей обмотки возбуждения. Так как поток рассеяния замыкается на немагнитной среде, ЭДС es рассматривают как ЭДС самоиндукции и определяют по выражению: 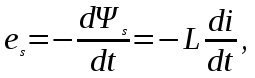 (5.6) (5.6)где LS =ψS/i. Исходя из этого рассуждения реальную катушку можно представить как бы состоящей из двух последовательно соединенных катушек рис. 1  Рисунок 5.14 - Схема замещения катушки с ферромагнитным сердечником Первая из них является линейной катушкой с активным сопротивлением Rоб и индуктивностью Ls, а вторая – идеализированной катушкой с числом витков w, активное сопротивление которой равно нулю. Поток этой катушки замыкается только по сердечнику, и напряжение на ней u΄ = -e. Зависимость u΄ от тока катушки i нелинейная, следовательно, ее индуктивность не является постоянной величиной. Форма кривой тока идеализированной катушки с ферромагнитным сердечником при синусоидальном напряжении. На вход катушки приложено синусоидальное напряжение 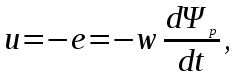 (5.7) (5.7)где ψр = wфp. Из уравнен6ия (5.7):  . .Или 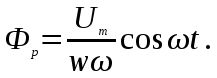 Заменяют: 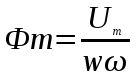 и получают и получают  (5.8) (5.8)где Следовательно магнитный поток Фр=Ф и изменяеться по синусоидальному законуи отстает от приложенного напряжения на угол 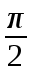 . .По известному напряжению U можно определить форму кривой тока идеализированной магнитной цепи. Для этого из семейства динамических петель нужно выбрать такую, у которой вершина соответствует амплитуде магнитной индукции. Затем на одной плоскости следует совместить динамическую петлю и кривую 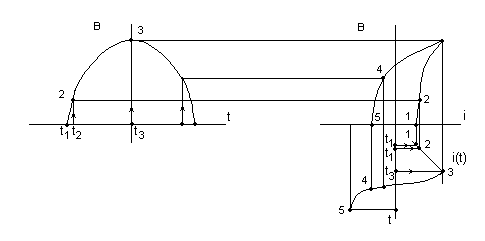 Рисунок 5.15 Построение кривой тока в катушке при синусоидальном напряжении Форма кривой тока получилась несинусоидальной. Это затрудняет количественный анализ процессов в электрических и магнитных цепях. Поэтому реальный несинусоидальный ток заменяют эквивалентным синусоидальным током при условии равенства их действующих значений. В некоторых случаях несинусоидальный ток заменяют его первой гармоникой. Векторная диаграмма и схема замещения идеализированной магнитной цепи. Введение понятия эквивалентного тока позволяет построить векторную диаграмму, построение которой начинают с вектора магнитного потока Фm. Переменный синусоидальный поток индуктирует Эдс Eр=Е в намагничивающей обмотке возбуждения, которая отстает по фазе от вектора Фm на угол 90 градусов , рисунок 5.16. Эдс 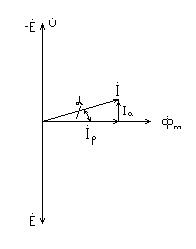 Рисунок 5.16 - Векторная диаграмма идеализированной катушки. Векторной диаграмме соответствует электрическая схема замещения рисунке 5.17. 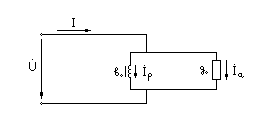 Рисунок 5.17 - Схема замещения идеализированной катушки Векторную диаграмму катушки можно видоизменить, разложив на составляющие напряжение  Рисунок 5. 18 - Векторная диаграмма Этой векторной диаграмме соответствует последовательная схема замещения катушки, рисунок 5.19. 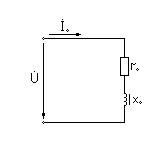 Рисунок 5.19 - Схема замещения идеализированной катушки с последовательным соединением элементов. Реальная магнитная цепь. Реальная магнитная цепь имеет активное сопротивление обмотки и магнитное поле рассеяния, которое к некоторых случаях приходиться учитывать. После замены несинусоидального тока эквивалентным синусоидальным током уравнение (5.7) можно записать для комплексных действующих значений: Данному уравнению соответствует следующая векторная диаграмма и схема замещения: 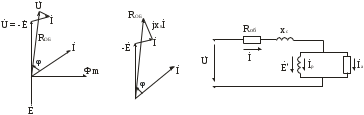 Рисунок 5.20 - Векторная диаграмма и схема замещения реальной магнитной цепи. Вопросы для самоконтроля Что называется магнитными цепями? Какие бывают свойства магнитных материалов? Какие существуют законы магнитных цепей? Какова классификация магнитных цепей? Каковы особенности расчета и анализа неразветвленных магнитных цепей? |
