ЛР 1 Трофимов Ю. Анализ характеристик листовой рессоры локомотива
 Скачать 470.42 Kb. Скачать 470.42 Kb.
|
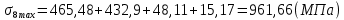 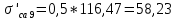 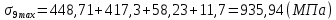 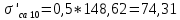 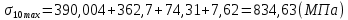 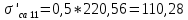 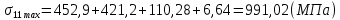 По окончании расчётов необходимо на миллиметровой бумаге начертить рассчитанную листовую рессору с указанием основных линейных параметров. Масштаб длин листов рессоры взять 1:4 или 1:5. Масштаб для толщины листа взять 1:1 или 1:2. На этом же листе сделать таблицу со следующими параметрами по отдельным листам рессоры: 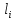 , см; , см; 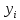 , см; , см; 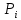 , кН; , кН; 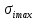 , МПа. , МПа.Количество листов:  (1.8) (1.8)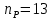 (листов) (листов)Количество листов принимается с округлением в меньшую сторону и дополнительным вычитанием одного листа. Общее количество листов разбивается на количество коренных листов m и количество ступенчатых рессор n. При определении количества коренных листов необходимо придерживаться следующего правила: если общее количество листов рессор меньше восьми включительно, брать два коренных листа; в других случаях – три. m = 3, n = 10 Шаг удлинения листов, см:  (1.9) (1.9)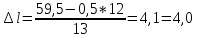 (см) (см)Полученный шаг удлинения листов округляется с шагом 0,5 см. Например, если получилось 4,9 см, то округлить до 5,0 см, если получилось 5,7 см, то округлить до 5,5 см. Длина первого ступенчатого листа (самого длинного), см:  (1.10) (1.10)где i = m+1 – номер первого ступенчатого листа. 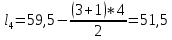 (см) (см)Полученную длину первого ступенчатого листа округляем в меньшую сторону до целого значения. Длины остальных листов ступенчатой части, см:  (1.11) (1.11)где i – шаг расчёта ступенчатого листа, i = n–m–1…1 (с шагом минус 1).  0,5 * 12 + 9 * 0,5 * 12 + 9 * 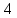 = 42 (см) = 42 (см) 0,5 * 12 +8 * 0,5 * 12 +8 * 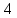 = 38 (см) = 38 (см) 0,5 * 12 + 7 * 0,5 * 12 + 7 * 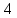 = 34 (см) = 34 (см) 0,5 * 12 + 6 * 0,5 * 12 + 6 * 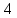 = 30 (см) = 30 (см) 0,5 * 12 + 5* 0,5 * 12 + 5* 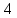 = 26 (см) = 26 (см) 0,5 * 12 + 4 * 0,5 * 12 + 4 * 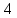 = 22(см) = 22(см) 0,5 * 12 + 3 * 0,5 * 12 + 3 * 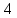 = 18 (см) = 18 (см) 0,5 * 12 + 2* 0,5 * 12 + 2* 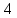 = 14 (см) = 14 (см) 0,5 * 12 + 1 * 0,5 * 12 + 1 * 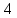 = 10 (см) = 10 (см)Момент инерции сечения листа, см4:  (1.12) (1.12) = 4,1 (см4) = 4,1 (см4)Действительный статический прогиб без учета сил трения, см:  , (1.12) , (1.12)где ln – натуральный логарифм. 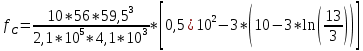 = 4,54 (см) = 4,54 (см)Коэффициент динамичности прогибов:  (1.13) (1.13)Результаты расчёта величин КДП для различных значений μ и РТ/Ра сводим в таблицу 1. Коэффициент динамичности прогибов для μ=0,4, PТ/Pa = 1: 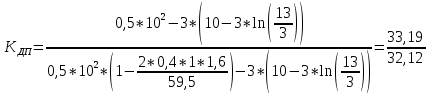 = 1,03 = 1,03Коэффициент динамичности прогибов для μ=0,4, PТ/Pa=fc/ya=4,54/3,4=1,33=1: 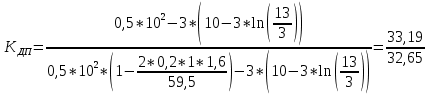 = 1,01 = 1,01Коэффициент динамичности напряжений:  (1.14) (1.14)Результаты расчёта величин КДН для различных значений μ, РТ/Ра и РС/Ра сводим в таблицу 1. Коэффициент динамичности напряжений при μ = 0,4 и Pc/Pa = 1: 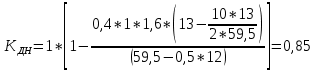 Коэффициент динамичности напряжений при μ = 0,2 PТ/Pa=fc/ya=4,54/3,4=1,33=1: 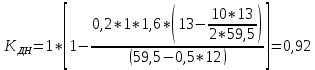 Таблица 1. Коэффициенты динамичности. Результаты расчёта величин  для различных значений для различных значений  , ,  и и  сводим в таблицу 1. сводим в таблицу 1.Таблица 1. Коэффициенты динамичности
Диапазон разброса статического прогиба при учете сил трения, см:  (1.15) (1.15) принимается по табл. 1 при μ = 0,4 и PТ/Pa = 1. принимается по табл. 1 при μ = 0,4 и PТ/Pa = 1.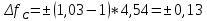 (см) (см)Расчётный чертежный статический прогиб, см: 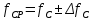 (1.16) (1.16)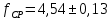 (см) (см)Статическая жесткость рессоры, кН/см:  (1.17) (1.17)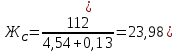 кН/см) кН/см)Динамическая жесткость пружины, кН/см:  (1.18) (1.18)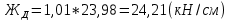  определяется интерполяцией по табл. 1 при μ = 0,2 и PТ/Pa = fc/ya=4,54/3,4=1,43=1. определяется интерполяцией по табл. 1 при μ = 0,2 и PТ/Pa = fc/ya=4,54/3,4=1,43=1.Статическое напряжение, МПа:  (1.19) (1.19)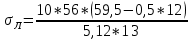 = 450,12 (МПа) = 450,12 (МПа)Расчетные статические напряжения в зоне края хомута, МПа:  (1.20) (1.20) принимается по табл. 1 при μ = 0,4 и Pc/Pa = 1. принимается по табл. 1 при μ = 0,4 и Pc/Pa = 1. 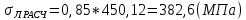 Амплитуда динамических напряжений, МПа:  (1.21) (1.21)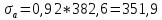 (МПа) (МПа) определяется интерполяцией по табл. 1 при μ = 0,2 и Pc/Pa = fc/ya. определяется интерполяцией по табл. 1 при μ = 0,2 и Pc/Pa = fc/ya.Расчет статических усилий, действующих на отдельные листы рессоры, и напряжений в них Расчет прогибов для сечений, в которых оканчиваются листы коренной и ступенчатой части, см:  (2.1) (2.1)где lni – длины листов рессоры, определяемые по формулам (1.3), (1.10) и (1.11). 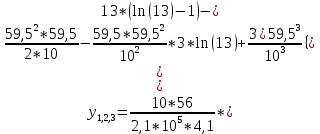 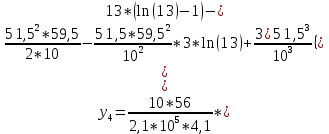 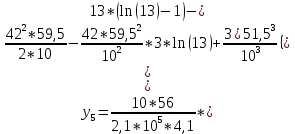 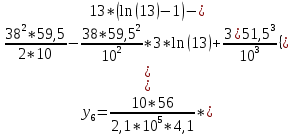 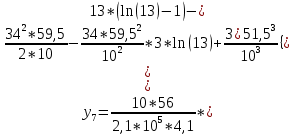 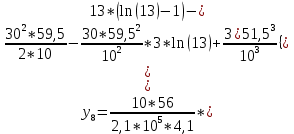 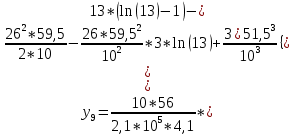 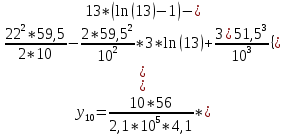 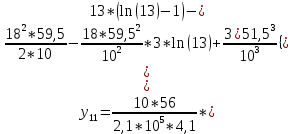 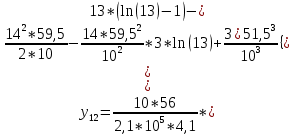 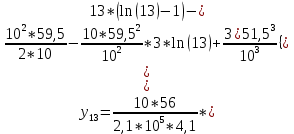 Расчет усилий, действующих на отдельные листы, ступенчатой части, кН: 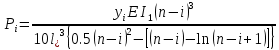 (2.2) (2.2)где i – шаг пересчёта листов ступенчатой части. i = 1÷n. При i = n равенство обращается в ноль, поэтому на последнем шаге необходимо принять i = n – 0.001. 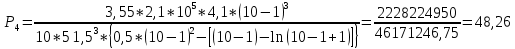 (кН) (кН)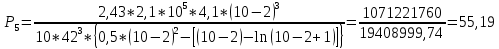 (кН) (кН)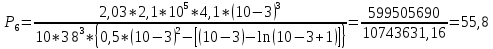 (кН) (кН)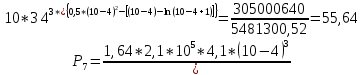 (кН) (кН)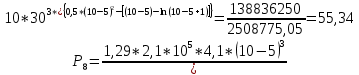 (кН) (кН)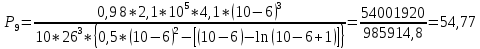 (кН) (кН)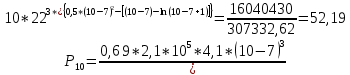 (кН) (кН)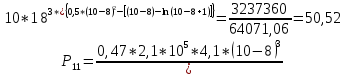 (кН) (кН)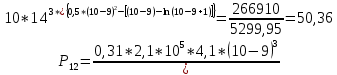 (кН) (кН)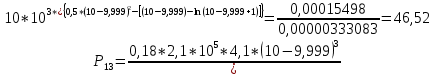 (кН) (кН)Расчет напряжений в отдельных листах, МПа. В коренных листах: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
, 