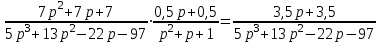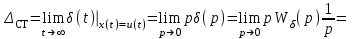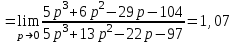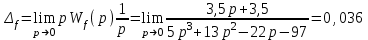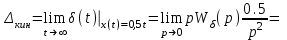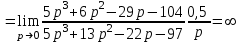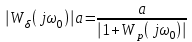Теория автоматического управления на тему: Анализ одноконтурной системы автоматического регулирования. Анализ одноконтурной системы автоматического регулирования
 Скачать 208.31 Kb. Скачать 208.31 Kb.
|
|
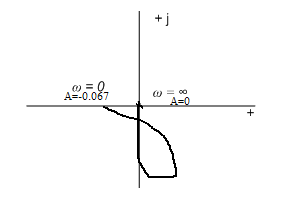
МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» (ФГБОУ ВО «СамГТУ») филиал ФГБОУ ВО «СамГТУ» в г. Новокуйбышевске Кафедра: Электроэнергетика, электротехника и автоматизация технологических процессов КУРСОВАЯ РАБОТА по дисциплине: Теория автоматического управления на тему: Анализ одноконтурной системы автоматического регулирования Выполнил студент 3 курса, группы 41-НФ17уС Направление: 15.03.04 Автоматизация технологических процессов и производств Митюрин Алексей Александрович Руководитель: Заведующий кафедрой Шишков Евгений Михайлович Работа защищена «____» ______________ 2020 г. Оценка ___________________ Новокуйбышевск 2020 МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» (ФГБОУ ВО «СамГТУ») филиал ФГБОУ ВО «СамГТУ» в г. Новокуйбышевске Кафедра: Электроэнергетика, электротехника и автоматизация технологических процессов ОТЗЫВ руководителя на курсовую работу студента 3 курса 41-НФ17уС группы Митюрина Алексея Александровича Направление подготовки: 15.03.04 Автоматизация технологических процессов и производств Профиль: Автоматизация технологических процессов и производств Руководитель: Шишков Евгений Михайлович, заведующий кафедрой Дисциплина: Теория автоматического управления Тема курсовой работы: Анализ одноконтурной системы автоматического регулированияСодержание: 1. По заданной системе уравнений построить математическую модель описания САР в форме структурной схемы. 2. Преобразовать полученную структурную схему к одноконтурному виду. 3. Определить передаточную функцию (ПФ) и выражения для частотных характеристик разомкнутой системы: амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ). 4. Построить ожидаемые асимптотическую логарифмическую амплитудно-частотную и логарифмическую фазо-частотную характеристики (ас. ЛАЧХ и ЛФЧХ), а также АФХ разомкнутой системы. 5. Построить точные характеристики разомкнутой системы: ЛАЧХ, ЛФЧХ, АФХ. Сравнить их с ожидаемыми характеристиками, полученными в п.4. 6. По частотным характеристикам разомкнутой системы, полученным в п.5, определить для замкнутой системы запас по фазе 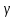 , запас по модулю β и предельный коэффициент усиления Кпр и дать заключение об её устойчивости. , запас по модулю β и предельный коэффициент усиления Кпр и дать заключение об её устойчивости.7. Определить Кпр с помощью одного из алгебраических критериев устойчивости и сравнить его значение с полученным в п.6. 8. Найти передаточные функции ошибки в замкнутой системе по управляющему воздействию x(t) и возмущению f(t). Определить статическую, кинетическую, динамическую ошибки по управляющему воздействию и статическую ошибку по возмущению. Статические ошибки определяются при единичных ступенчатых воздействиях x(t) = u(t), f(t)= u(t), кинетическая ошибка – при x(t) = 0,5t , динамическая ошибка по амплитуде – при гармоническом воздействии x(t) = asin ω0 t с a = 1, ω0 = 0,1 ωср , где ωср - частота среза. Наличие самостоятельных разработок автора В соответствии с заданием на проектирование. Практическая значимость В соответствии с заданием на проектирование. Недостатки __________________________________________________________________________________________________________________________________________________________________________ Оценка _____________________________________________________________________________________ «_____»__________2020 г. ___________________ (дата) (подпись) МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» (ФГБОУ ВО «СамГТУ») филиал ФГБОУ ВО «СамГТУ» в г. Новокуйбышевске Кафедра: Электроэнергетика, электротехника и автоматизация технологических процессов ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студент: Митюрин Алексей Александрович. Курс, группа: 3, 41-НФ17уС Направление подготовки: 15.03.04 Автоматизация технологических процессов и производств Профиль: Автоматизация технологических процессов и производств Руководитель: Шишков Евгений Михайлович, заведующий кафедрой Дисциплина: Теория автоматического управления Тема курсовой работы: Анализ одноконтурной системы автоматического регулированияЗадание: 1. По заданной системе уравнений построить математическую модель описания САР в форме структурной схемы. 2. Преобразовать полученную структурную схему к одноконтурному виду. 3. Определить передаточную функцию (ПФ) и выражения для частотных характеристик разомкнутой системы: амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ). 4. Построить ожидаемые асимптотическую логарифмическую амплитудно-частотную и логарифмическую фазо-частотную характеристики (ас. ЛАЧХ и ЛФЧХ), а также АФХ разомкнутой системы. 5. Построить точные характеристики разомкнутой системы: ЛАЧХ, ЛФЧХ, АФХ. Сравнить их с ожидаемыми характеристиками, полученными в п.4. 6. По частотным характеристикам разомкнутой системы, полученным в п.5, определить для замкнутой системы запас по фазе 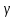 , запас по модулю β и предельный коэффициент усиления Кпр и дать заключение об её устойчивости. , запас по модулю β и предельный коэффициент усиления Кпр и дать заключение об её устойчивости.7. Определить Кпр с помощью одного из алгебраических критериев устойчивости и сравнить его значение с полученным в п.6. 8. Найти передаточные функции ошибки в замкнутой системе по управляющему воздействию x(t) и возмущению f(t). Определить статическую, кинетическую, динамическую ошибки по управляющему воздействию и статическую ошибку по возмущению. Статические ошибки определяются при единичных ступенчатых воздействиях x(t) = u(t), f(t)= u(t), кинетическая ошибка – при x(t) = 0,5t , динамическая ошибка по амплитуде – при гармоническом воздействии x(t) = asin ω0 t с a = 1, ω0 = 0,1 ωср , где ωср - частота среза. Вариант № __11__. Рекомендуемая литература: Лысов В.Е., Пешев Я.И. Теоретические основы дискретных систем автоматического управления: учебное пособие / В. Е. Лысов, Я. И. Пешев, Самар.гос.техн.ун-т, Электропривод и промышленная автоматика.- Самара: 2018.- 160 c Руководитель _____________ /Е.М. Шишков/ Студент ________А.А. Митюрин_________ Исходные данные. Задана система уравнений во временной области, описывающих работу системы автоматического управления: 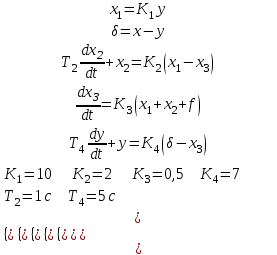 а) х1 = К1у б) δ=х-у в)T2dx2/dt + x2= K2 (х1 -x3) г) dx3/dt =К3(x1+x2+f) (1) д) T4dу/dt + у = K4 (δ-x3) Параметры системы (1): K1 =10; K2 = 2; K3 = 0,5; K4 = 7; T2 = 1c; T4 = 5с. Выполнение расчета. 1. Преобразуем левые и правые части уравнений системы (1) по Лапласу с учетом, что все переменные при t<0 равны нулю: а) X1(p)= К1Y(p) б) δ(p)= X(p)-Y(p)) в) T2 р X2(p)+ X2(p)=К2(X1(p)-X3(p)) (2) г) pX3(p) = К3(X1(p)+X2(p)+F(p)) д) T4 pY(p) + Y(p)= K4 (δ(p)-X3(p)) Представим каждое уравнение системы (2) типовыми соотношениями элементов структурной схемы САР: а) X1(p)= W1 (p)Y(p) б) δ(p)= X(p)-Y(p)) в) X2(p)= 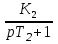 (X1(p)-X3(p))=W2(p) (X1(p)-X3(p (3) (X1(p)-X3(p))=W2(p) (X1(p)-X3(p (3)г) X3(p) = 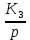 (X1(p)+X2(p)+F(p))=W3(p)(X1(p)+X2(p)+F(p)) (X1(p)+X2(p)+F(p))=W3(p)(X1(p)+X2(p)+F(p))д) Y(p)= 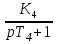 (δ(p)-X3(p))=W4(p) (δ(p)-X3(p)) (δ(p)-X3(p))=W4(p) (δ(p)-X3(p))Отобразим каждое из уравнений системы (3) соответствующим элементом структурной схемы. В результате получим структурную схему системы (1) (рис. 1, а). 2. Преобразуем структурную схему (рис. 1, а) к одноконтурному виду. Для этого произведем последовательно ряд эквивалентных структурных преобразований, сохраняющих неизменными связь между переменными x, y, δ, f (рис. 1, б). Последовательное соединение звеньев с ПФ W1(p) и W2(p) представим звеном с эквивалентной ПФ W5(p)= W1(p)⸱W2(p) (рис. 1,в); звенья с ПФ W2(p) и W3(p), соединенное в цепь обратной связи, представим одним звеном с эквивалентной ПФ W6(p)=W3(p)/(1+W2(p)⸱W3(p)) (рис.1,г), параллельное соединение звеньев с ПФ W1(p) и W5(p) представим звеном с эквивалентной ПФ W7(p)= W1(p)+W5(p) (рис. 1,д); звенья с ПФ W4(p), W7(p) и W6(p), соединенное в цепь обратной связи, представим одним звеном с эквивалентной ПФ W8(p)=W4(p)/(1-W4(p)⸱W6(p) W7(p)). В результате исходная структурная схема (рис. 1, а) представлена в одноконтурном виде (рис. 1, е). 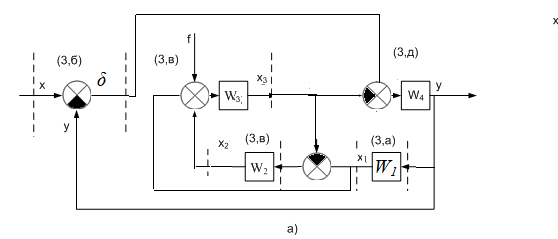 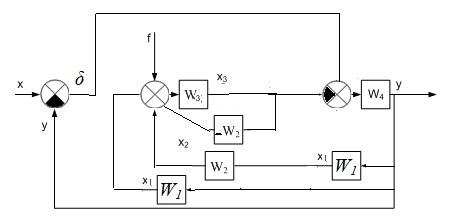 б) 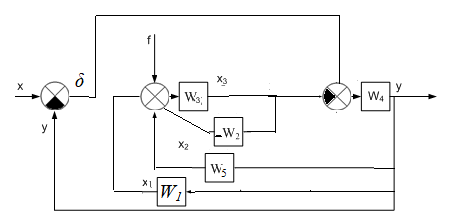 в) 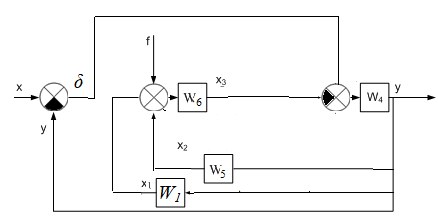 г) 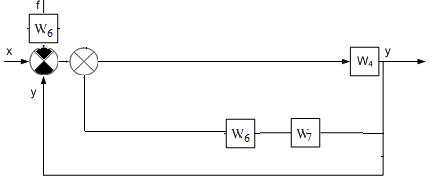 д) 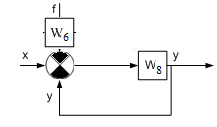 е) Рис.1 3. По структурной схеме (рис. 1, д) найдем ПФ разомкнутой системы как произведение ПФ всех звеньев, входящих в замкнутый контур: Wр(p)=W8(p)= 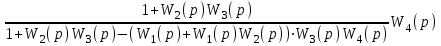 (4) (4)Подставим в (4) выражения ПФ из соотношений (3), преобразуем полученное выражение к дробно-рациональному виду и запишем его с учетом числовых значений параметров: Wр(p)= 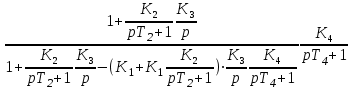 = == 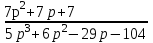 = =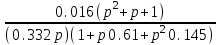 (5) (5)Найдем из (5) выражения для АФХ, АЧХ и ФЧХ разомкнутой системы: Wр(jω) = 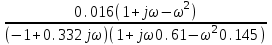 Модулемкомплексного числаz = x + iyназывается вещественное число|z|равное: A(ω) = | Wр(jω) | = 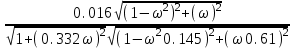 φ(ω) = argWр(jω) = arctg(ω/(1-ω2)) -π+ arctg(0.332ω)– arctgω(0.61ω/(1-ω20.145)) 4. Выражение для ЛАЧХ имеет вид: L(ω)=20lgA(ω)=20lg0.016+20lg 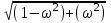 –20lg –20lg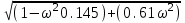 - - -20lg 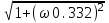 (6) (6)Построим ас. ЛАЧХ, пользуясь следующим приемом: в зависимости от значения частоты под знаком радикала пренебрегаем меньшим из двух слагаемых. Очевидно, что каждому радикалу соответствуют два диапазона частот со своим значением сопрягающей (граничной) частоты, при которой изменяется соотношение между значениями слагаемых. Для радикала вида 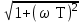 оно равно оно равно 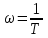 . Найдем сопрягающие частоты: . Найдем сопрягающие частоты:ω1=1/1 = 1 c-1; ω2 =1/√0.165 = 2.46 c-1; ω3 =1/0.332 = 3.01c-1. Запишем выражения для ас. ЛАЧХ 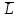 в различных диапазонах частот. в различных диапазонах частот.1) 0 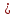 ω ω 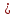 ω1 ; 1>(ω0.332)2 ; 1 > ω2 ; 1 > (ω0.406)2 ω1 ; 1>(ω0.332)2 ; 1 > ω2 ; 1 > (ω0.406)2 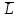 1 = 20lg0.016 1 = 20lg0.016 2) ω 1 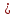 ω ω 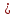 ω2 ; 1<(ω)2 ; 1 > (ω0.332)2 ; 1 > (ω0.406)2 ω2 ; 1<(ω)2 ; 1 > (ω0.332)2 ; 1 > (ω0.406)2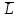 2 = 20lg0.016 +40lgω = 2 = 20lg0.016 +40lgω = 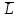 1 +40lgω 1 +40lgω3) ω 2 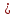 ω ω 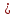 ω3; 1<(ω)2 ; 1 > (ω0.332)2 ; 1 <(ω0.406)2 ω3; 1<(ω)2 ; 1 > (ω0.332)2 ; 1 <(ω0.406)2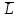 3 = 20lg 0.016 +40lg ω– 40l ω0.406 = 3 = 20lg 0.016 +40lg ω– 40l ω0.406 = 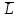 2 -40lg0.406 2 -40lg0.4064) ω 3 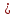 ω ω 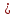 ∞; 1<(ω)2 ; 1 < (ω0.332)2 ; 1 <(ω0.406)2 ∞; 1<(ω)2 ; 1 < (ω0.332)2 ; 1 <(ω0.406)2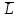 4 = 20lg0.016 +40lgω– 40lgω0.406 – 20 lgω0.322 = 4 = 20lg0.016 +40lgω– 40lgω0.406 – 20 lgω0.322 = 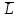 4 – 20lgω0.332 4 – 20lgω0.332Ас. ЛАЧХ и ЛФЧХ представлены на рис.2. На рис.3 представлен ожидаемый характер изменения АФХ. Из них следует следующее асимптотическое поведение частотных характеристик: при ω → 0 : A(ω) → -0.067, φ(ω) → -π; при ω → ∞ : A(ω) → 0, φ(ω) →-π/2. 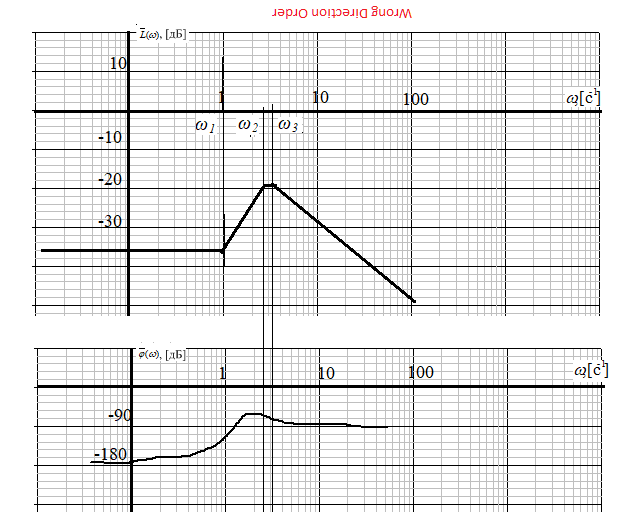 Рис. 2 |

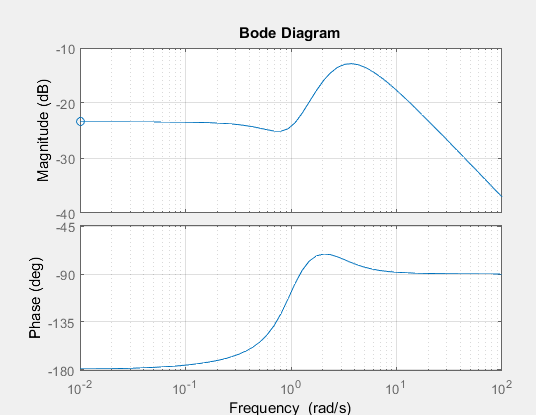
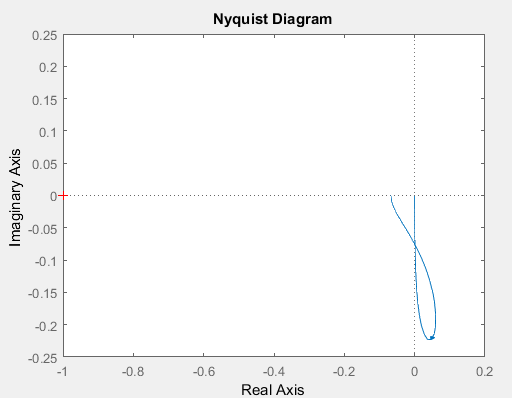
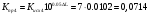
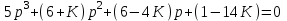 .
.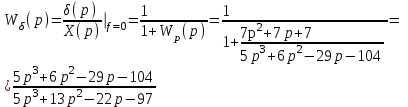
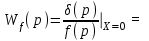
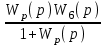 =
=