Анализ панельных данных. Анализ панельных данных Область применения
 Скачать 160.21 Kb. Скачать 160.21 Kb.
|
|
Анализ панельных данных 1. Область применения Термин "панельные данные" (panel data) пришел из обследований индивидов, и в этом контексте "панель" представляла собой группу индивидов, за которыми регулярно осуществляли наблюдения в течение определенного периода времени. В настоящее время методы анализа панельных данных получили большое распространение, и понимание панельных данных стало намного шире. Наряду с термином "панельные данные" иногда также используется термин "лонгитюдные данные" (longitudinal data). Панельные данные состоят из повторных наблюдений одних и тех же выборочных единиц, которые осуществляются в последовательные периоды времени. В качестве объектов наблюдения могут выступать индивиды, домашние хозяйства, фирмы, страны и т.д. Примером панельных данных могут быть ежегодные обследования одних и тех же домашних хозяйств или индивидов (например, для определения изменения их благосостояния), ежеквартальные данные об экономической деятельности отдельных компаний, ежегодные социально-экономические показатели для регионов одной страны или для группы стран и т.д. Панельные данные совмещают в себе как пространственные данные, так и временные ряды и сочетают достоинства каждого их этих видов данных. Это позволяет строить более адекватные и содержательные модели для изучения истинной причинно-следственной связи между различными переменными, что представляется невозможным в рамках только временных или только пространственных данных. Выделяют следующие преимущества использования панельных данных. 1. Панельные данные позволяют учитывать индивидуальную неоднородность. Временные ряды или пространственные данные не всегда позволяют учесть неоднородность индивидов, фирм, регионов или стран, что может привести к смещенным оценкам. Так, например, в исследовании Б. Балтаги и Д. Левина[1] изучался спрос на сигареты в США. Спрос моделировался как функция от лагов потребления, цены и дохода. Эти переменные отличались по штатам и во времени. Однако существовало множество других факторов, различающихся по штатам или во времени, которые могли оказывать влияние на потребление, например такие факторы, как религия, образование и реклама на телевидении и радио. При измерении этих переменных для каждого штата и периода времени возникают определенные трудности и очень сложно достигнуть того, чтобы их можно было включить в уравнение потребления. Однако пропуск этих переменных приведет к смещению в оценках. Панельные данные способны учитывать переменные, отличающиеся по штатам и во времени, вне зависимости от того, измеряемы они или нет, в то время как временные ряды или пространственные данные не позволяют этого сделать. Таким образом, панельные данные дают возможность избежать ошибки спецификации, возникающей из-за того, что существенные переменные не включены в модель. 2. Панельные данные содержат большое число наблюдений и тем самым предоставляют исследователю большее количество информации, им свойственна большая вариация и меньшая коллинеарность объясняющих переменных, они дают большее число степеней свободы и обеспечивают большую эффективность оценок. При анализе временных рядов исследователи часто сталкиваются с мультиколлинеарностью факторов. Например, в рассмотренном выше случае со спросом на сигареты существовала высокая зависимость между ценой и доходом в агрегированных временных рядах для США. Высокая коллинеарность между этими факторами будет менее вероятна при использовании панельных данных по штатам, так как пространственное измерение немного увеличивает вариацию факторов и делает более информативными данные по цене и доходу. Действительно, вариация в данных может быть разложена на две составляющие: вариацию между штатами разных размеров и с различными характеристиками и вариацию внутри штатов, при этом последняя обычно всегда больше. К тому же более информативные данные могут привести к более надежным оценкам параметров. 3. Панельные данные предоставляют возможность изучать динамику изменений индивидуальных характеристик единиц совокупности. Панельные данные хорошо подходят для изучения перемены работы, периода безработицы, изменений в доходах, для исследования длительности пребывания в определенном экономическом состоянии, например в бедности или в качестве безработного, а также могут помочь изучить скорость приспособления индивидов к изменениям в экономической политике. Так, при измерении безработицы пространственные данные позволяют оценить, какую долю в совокупности составляют безработные в конкретный момент времени; временные данные могут показать, как эта доля менялась во времени; и только панельные данные позволяют оценить, какая доля тех, кто являлся безработным в один период, останется безработным в другой период. Панельные данные могут использоваться как для объяснения того, почему различные единицы совокупности ведут себя по-разному, так и для того, чтобы определить, почему конкретная единица совокупности ведет себя по-разному в различные периоды времени. 4. Панельные данные лучше способны идентифицировать и измерить эффекты, которые просто не определяемы только во временных рядах или только в пространственных данных. В качестве примера может выступать исследование того, происходит ли увеличение или уменьшение заработной платы за счет членства в профсоюзе. На этот вопрос лучше всего ответить, если мы наблюдаем переход работника с работы с профсоюзом на работу без профсоюза или наоборот, а это могут отразить только панельные данные. Рассматривая индивидуальную характеристику работника в качестве константы, можно будет определить, оказывает ли влияние членство в профсоюзе на зарплату и насколько. Подобный анализ может также использоваться для оценки других типов дифференциации зарплаты, например, для оценки премии, выплачиваемой за опасную или неприятную работу. 5. Панельные данные позволяют конструировать и тестировать более сложные поведенческие модели, чем пространственные данные и временные ряды в отдельности. Например, техническая эффективность лучше изучается и моделируется с панельными данными. Также в панелях может быть наложено меньше ограничений на модели распределенного лага, которые обычно рассматриваются во временных рядах. 6. Панельные данные позволяют избежать смещения, связанного с агрегированием данных, так как панельные данные, собранные на микроуровне (по индивидам, фирмам или домашним хозяйствам), могут быть измерены более точно, чем аналогичные переменные, полученные на макроуровне. При этом во временных рядах рассматривается изменение во времени характеристик некоторой усредненной репрезентативной единицы совокупности, а в пространственных данных не учитываются ненаблюдаемые индивидуальные характеристики единиц совокупности. 7. Панельные данные макроуровня имеют более длинные временные ряды, и панельные тесты на единичный корень имеют стандартные асимптотические распределения в отличие от проблемы нестандартных распределений, типичной для теста на единичный корень в анализе временных рядов. Однако у панельных данных есть и недостатки. Определенные проблемы связаны со сбором данных: проблема покрытия, т.е. неполный учет интересующей совокупности; отсутствие отклика, которое может быть связано как с отсутствием взаимодействия с респондентом, так и с ошибкой интервьюера, искажения, связанные с ошибками измерения, которые могут возникнуть по причине неправильного ответа из-за неясной формулировки вопроса, ошибок памяти, намеренного искажения ответа (престижное смещение), неподходящих информантов, ошибочной записи ответов и эффектов интервьюера. Отсутствие данных может быть вызвано различными причинами. Например, если индивиды выбирают, что им не стоит работать, потому что предлагаемая зарплата ниже минимального размера оплаты труда, то в этом случае для этих индивидов будут отсутствовать данные по зарплате, но будут иметься данные по другим характеристикам. Так как пропущена только их зарплата, то выборка будет цензурированной. Однако если мы не наблюдаем всех данных этих индивидов, то выборка будет уже усеченной, и в результате получатся смещенные оценки. В первой волне панели отсутствие отклика может быть связано с тем, что выбранный индивид или домохозяйство отказались участвовать в опросе или просто никого не оказалось дома. Частичное отсутствие отклика возникает, когда не дан ответ на один или несколько вопросов. В последующих волнах панели вследствие отсутствия отклика может возникнуть проблема истощения данных, когда респондент, ранее принимавший участие в опросах, может умереть, переехать на другое место жительства или обнаружить, что затраты на участие в опросе для него стали слишком большими, и отказаться от дальнейшего участия. В настоящее время панельные обследования в разных формах проводятся во многих странах. Впервые панельные данные начали формироваться в США в 1960-х гг. Среди наиболее известных баз панельных данных США можно выделить PSID и NLS. Панельное исследование динамики доходов (The US Panel Study of Income Dynamics (PSID), psidonline.isr.umich.edu/)– база панельных данных по американским домохозяйствам, собираемая Институтом социальных исследований Мичиганского университета. База PSID появилась в 1968 г. и включала данные по 4800 семьям. В настоящее время она охватывает около 9000 американских семей. Данные содержат более 5000 переменных по экономике, демографии, здоровью и социальному поведению. Национальные лонгитюдные исследования (National Longitudinal Surveys (NLS), bls.gov/nls/horrktm) – панельные исследования, спонсируемые Бюро трудовой статистики США, которые начали проводиться с 1966 г. На примере нескольких групп мужчин и женщин изучаются различные аспекты активности на рынке труда и другие значительные события в жизни этих людей. Европейские панельные данные стали появляться только в 1980-х гг. Так, например первая волна панельного обследования Немецкой социально-экономической панели (Soziooekonomisches Panel (SOEP), diw.de/soep), формируемой Немецким институтом экономических исследований (Deutsches Institut fiir Wirtschaftsforschung (DIW), Berlin), состоялась в 1984 г. и охватила более 5000 западногерманских домохозяйств. В настоящее время это обследование содержит данные около 11 000 домохозяйств, которые включают в себя демографические переменные, зарплату, доход, выплату пособий, уровень удовлетворенности различными аспектами жизни, надежды и страхи, политическую активность и т.д. С 1991 г. Институтом социальных и экономических исследований Эссекского университета проводится панельное исследование британских домохозяйств (The British Household Panel Survey (BHPS), iser.essex.ac.uk/survey/bhps). Это национальная репрезентативная выборка 5500 домохозяйств и 10 300 индивидов, выбранных из 250 районов Великобритании. Эти данные отражают демографические характеристики домохозяйств, рынок труда, здоровье, образование, жилищные условия, потребление, доход и т.д. В 1994– 2001 гг. при содействии Евростата проводилось Европейское панельное обследование домохозяйств (The European Community Household Panel (ECHP), epunet.essex.ac.uk/echpphp), в рамках которого в странах, являющихся членами Евросоюза, собирались данные домохозяйств по доходу, работе и безработице, бедности, жилью, здоровью и т.д. В России панельные обследования стали проводиться в 1990-х г. Наиболее известной базой панельных данных является РМЭЗ – Российский мониторинг экономического положения и здоровья населения (Russia Longitudinal Monitoring Survey (RLMS), cpc.unc.edu /projects / rims). РМЭЗ представляет собой серию общенациональных репрезентативных опросов домохозяйств и индивидов, проводившихся в России с 1992 г. Данные обследований содержат ответы на более чем 3000 вопросов, касающихся доходов и расходов, материального благосостояния, занятости, уровня образования, состояния здоровья и т.д. 2. Модели панельных данных и основные обозначения Пусть имеются данные 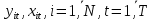 . Здесь N – количество субъектов, а Т – число последовательных моментов времени. Требуется оценить модель линейной связи между переменными Y и X. В общем случае Х является вектором конечной размерности k (может существовать p независимых факторов). . Здесь N – количество субъектов, а Т – число последовательных моментов времени. Требуется оценить модель линейной связи между переменными Y и X. В общем случае Х является вектором конечной размерности k (может существовать p независимых факторов).Рассмотрим сбалансированные панели, где для каждой пространственной единицы имеется одинаковое число наблюдений по всем периодам времени. Тогда общее число наблюдений будет NT. При N=1 и достаточно большом Т получаются временные ряды, а при Т=1 и достаточно большом N получаются пространственные данные. Метод оценивания панельных данных относится к случаю, когда N>1 и Т >1. Будем рассматривать панельные данные с короткими временными рядами, где N намного больше Т, что очень часто встречается на практике, когда число наблюдаемых единиц достаточно велико (может достигать нескольких сотен или тысяч), а число моментов наблюдения ограничено. Для і-й единицы совокупности данные можно представить в виде 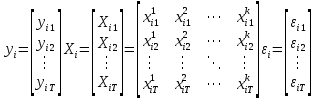 Тогда объединенные данные по всем единицам совокупности примут вид 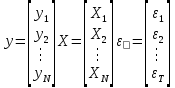 где у и ε – матрицы размерностью NT× 1, а X имеет размерность NT×k. 3. Модель пула При отсутствии значимых различий (неоднородности) между пространственными объектами выборки, возможно построение регрессии по объединенной выборке (pooled regression) – пула. Это модель сквозной регрессии: 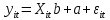 (1) (1)с остатками 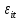 , удовлетворяющими требованиям МНК. В этом случае мы имеем дело с обычной линейной регрессией с NT наблюдениями, удовлетворяющей предположениям классической нормальной линейной модели. Для получения эффективных оценок вектора коэффициентов достаточно использовать обычный метод наименьших квадратов (OLS) . Полученные при этом оценки b и а являются наилучшими линейными несмещенными оценками (BLUE – best linear unbiased estimate) вектора β. При соответствующих предположениях о поведении значений объясняющих переменных, когда N → ∞ или/и T → ∞, эта оценка является также и состоятельной оценкой этого вектора. , удовлетворяющими требованиям МНК. В этом случае мы имеем дело с обычной линейной регрессией с NT наблюдениями, удовлетворяющей предположениям классической нормальной линейной модели. Для получения эффективных оценок вектора коэффициентов достаточно использовать обычный метод наименьших квадратов (OLS) . Полученные при этом оценки b и а являются наилучшими линейными несмещенными оценками (BLUE – best linear unbiased estimate) вектора β. При соответствующих предположениях о поведении значений объясняющих переменных, когда N → ∞ или/и T → ∞, эта оценка является также и состоятельной оценкой этого вектора. 4. Модель регрессии с фиксированным эффектом (fixed effect model) 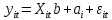 (2) (2)В отличие от предыдущего случая свободный член ai принимает различные значения для каждого объекта выборки. Смысл его в том, чтобы отразить влияние пропущенных или ненаблюдаемых переменных, характеризующих индивидуальные особенности исследуемых объектов не меняющиеся со временем. Термин "фиксированные эффекты" означает, что константа в уравнении регрессии может различаться между объектами, но для каждого конкретного объекта константа является постоянной во времени, т.е. не изменяется с течением времени t. Уравнение модели в матричной записи 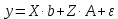 (3) (3)Размерности матриц: 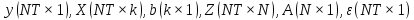 А -вектор констант, соответствующих детерминированным индивидуальным эффектам, а Z–блочно-диагональная матрица фиктивных переменных.  В этом случае оценка коэффициентов β 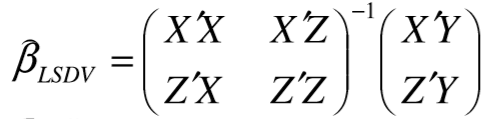 Считаются через обычный МНК. Эта модель является довольно гибкой, так как, в отличие от предыдущей модели, она позволяет учитывать индивидуальную гетерогенность объектов. Однако, за эту гибкость часто приходится расплачиваться потерей значимости оценок (из-за увеличения их стандартных ошибок), так как приходится оценивать N лишних параметров. Если количество субъектов анализа N велико, необходимость обращать матрицу высокой размерности (N+K) вызывает вычислительные трудности. Интересно, что численно те же самые значения оценок параметров β и а можно получить иным способом. Пусть 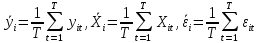 где под Х понимается вектор из всех факторов 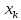 . То есть надо рассчитать средние по времени для каждого из факторов. Усредняя по времени обе части уравнения (2), получим . То есть надо рассчитать средние по времени для каждого из факторов. Усредняя по времени обе части уравнения (2), получим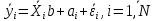 (4) (4)Из уравнений (2) и (4) получаем 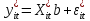 (5) (5)где 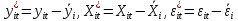 В результате мы получили модель, скорректированную на индивидуальные средние. Свободные члены оказались исключенными из уравнения. По полученному уравнению можно рассчитать параметр b. Эта оценка называется «внутригрупповой» («within-group» estimate), имея в виду, что она строится только на основании отклонений значений переменных от их средних по времени и тем самым принимает во внимание только изменчивость в пределах каждого субъекта, не обращая внимание на изменчивость между субъектами. Впрочем, в последнее время в эконометрической литературе чаще стали говорить об указанной оценке просто как о “within”-оценке. Получив параметр b, оценку ai можно получить 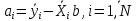 (6) (6)Полученные в итоге этих двух методов оценки а и b численно совпадают, но стандартные ошибки оценок β отличаются в этих двух моделях. При “within”-оценке стандартная ошибка меньше. А стандартные ошибки оценок αi, получаемые по (6), нельзя вычислять по формулам для стандартных ошибок оценок наименьших квадратов. Таким образом, β является состоятельной оценкой и когда N → ∞ и когда T → ∞, в то время как αi состоятельна только, когда T →∞ . Последнее есть следствие того, что оценивание каждого αi производится фактически лишь по T наблюдениям, так что при фиксированном T с ростом N происходит лишь увеличение количества параметров αi , но это не приводит к возрастанию точности оценивания каждого конкретного αi Для сравнения моделей будем сравнивать три модели. Мы будем говорить о модели M0 как о «модели без ограничений». Обозначим остаточную сумму квадратов SSост в этой модели как S0. 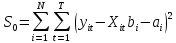 В рамках модели без ограничений рассмотрим две гипотезы: H1: βi одинаковы для всех i и равны β - модель с фиксированным эффектом - M1 с остаточной суммой квадратов SSост равной S1. H2: βi и αi одинаковы для всех i - модель пула – M2 с остаточной суммой квадратов SSост равной S2. М0: 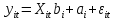 М1: 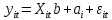 М2: 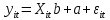 Проверка гипотезы H1 (следует ли использовать модель с фиксированными эффектами М1, либо строить модели отдельно для каждого объекта М0) 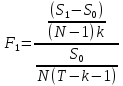 Если значение F1 статистически незначимо, то следует использовать модель с фиксированными эффектами. Если же значение F1 статистически значимо, то следует искать источник гетерогенности параметров, то есть модель с фиксированными эффектами использовать нельзя. Проверка гипотезы H2 (следует ли использовать единую модель для всех объектов М2, либо строить модели отдельно для каждого объекта М0) 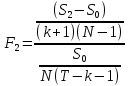 Если значение F2 статистически незначимо, то следует объединить данные в пул. Если же значение F2 статистически значимо, то следует искать источник гетерогенности параметров, то есть в пул объединять нельзя. Также можно сравнить модель пула и модель фиксированных эффектов. Проверка гипотезы H3 (тест Вальда). В рамках модели М1 проверяется гипотеза о равенстве всех ai при условии равенства всех βi 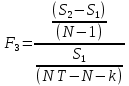 Если значение F3 статистически незначимо, то следует объединить данные в пул. Если же значение F3 статистически значимо, то следует использовать М1. 5. Модель регрессии со случайным эффектом (random effect model) В ряде ситуаций N субъектов, для которых имеются статистические данные, рассматриваются как случайная выборка из некоторой более широкой совокупности (популяции), и исследователя интересуют не конкретные субъекты, попавшие в выборку, а обезличенные субъекты, имеющие заданные характеристики. Соответственно, в таких ситуациях предполагается, что αi являются случайными величинами, и мы говорим тогда о модели со случайными эффектами (random effects). В такой модели αi уже не интерпретируются как значения некоторых фиксированных параметров и не подлежат оцениванию. Вместо этого оцениваются параметры распределения случайных величин αi 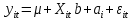 В матричной записи уравнение модели имеет вид 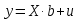 Размерности матриц: 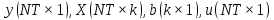 Здесь 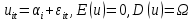 . .В такой форме модели ошибка 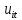 состоит из двух компонент αi и состоит из двух компонент αi и 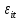 . Как и в модели с фиксированными эффектами, случайные эффекты αi также отражают наличие у субъектов исследования некоторых индивидуальных характеристик, не изменяющихся со временем в процессе наблюдений, которые трудно или даже невозможно наблюдать или измерить. Однако теперь значения этих характеристик встраиваются в состав случайной ошибки, как это делается в классической модели регрессии, в которой наличие случайных ошибок интерпретируется как недостаточность включенных в модель объясняющих переменных для полного объяснения изменений объясняемой переменной. . Как и в модели с фиксированными эффектами, случайные эффекты αi также отражают наличие у субъектов исследования некоторых индивидуальных характеристик, не изменяющихся со временем в процессе наблюдений, которые трудно или даже невозможно наблюдать или измерить. Однако теперь значения этих характеристик встраиваются в состав случайной ошибки, как это делается в классической модели регрессии, в которой наличие случайных ошибок интерпретируется как недостаточность включенных в модель объясняющих переменных для полного объяснения изменений объясняемой переменной.Здесь 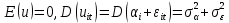 . .Ковариационная матрица u имеет вид  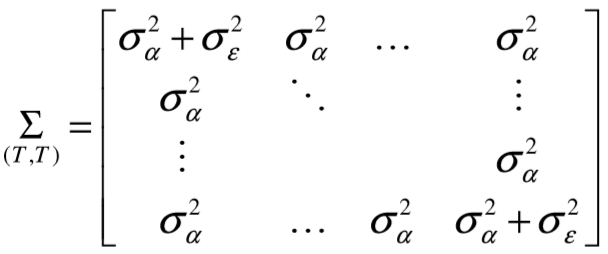 Таким образом, дисперсия y складывается из двух некоррелированных компонент: их называют компонентами дисперсии, а саму модель называют стандартной моделью со случайными эффектами (RE модель – random effects model). Эта модель является компромиссом между двумя предыдущими (пулом и моделью с фиксированными эффектами), поскольку она является менее ограничительной, чем первая модель, и позволяет получать более статистически значимые оценки, чем вторая. Если сформулированные предположения выполняются, оценки обобщенного метода наименьших квадратов (GLS) этой модели будут несмещенными. 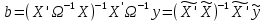 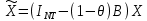 Здесь для преобразования переменных используется В-оператор. Оператор «Between» (B) - оператор усреднения по времени для отдельного объекта. Например, By. Если y имеет размерность (NT,1), то В будет размерности (NT,NT) и 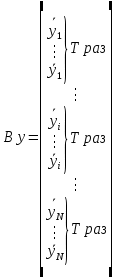 Также существует оператор вычисления отклонения от среднего по времени для отдельного объекта «Within» (W). 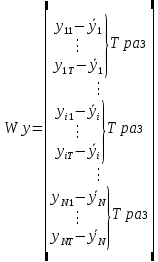 Используя эти операторы, можно показать, что переход к новым переменным в ОМНК осуществляется по формулам: 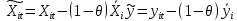 (7) (7)Где 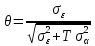 В анализе панельных данных принято вычислять оценки коэффициентов несколькими способами, и путем сравнения полученных результатов выбирать спецификацию, наиболее адекватную данным. В данном случае для оценки используется оператор В: Оценка «between» получается, если применить МНК к преобразованному под действием оператора В уравнению регрессии: 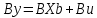 В предыдущем методе с фиксированными эффектами использовалась «within» оценка: 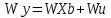 то есть мы переходили к новым переменным с использованием оператора W – из каждого значения вычитали среднее по времени по объекту. В модели со случайными эффектами оценки β находятся 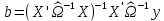 где 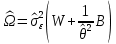 Таким образом, обобщенная оценка наименьших квадратов в RE-модели учитывает и внутригрупповую и межгрупповую изменчивость. Она является взвешенным средним “межгрупповой” оценки, учитывающей только межгрупповую изменчивость, и “внутригрупповой” оценки, учитывающей только внутригрупповую изменчивость, а коэффициент перед В измеряет вес, придаваемый межгрупповой изменчивости. Практически получить оценки для β можно следующим образом. Сначала найти среднее по времени для каждого из субъектов, потом по формуле (7) перейти к новым переменным. Для расчета θ требуются оценки 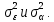 Для оценки 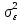 используют остаточную дисперсию из модели, скорректированной на индивидуальные средние, то есть из М1. используют остаточную дисперсию из модели, скорректированной на индивидуальные средние, то есть из М1. Оценить дисперсию 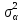 случайных эффектов можно, заметив, что при оценивании модели случайных эффектов можно, заметив, что при оценивании модели 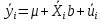 , приводящей к межгрупповой оценке , приводящей к межгрупповой оценке 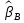 , дисперсия остатка для i-й группы равна , дисперсия остатка для i-й группы равна 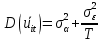 , откуда находим , откуда находим 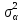 . . Алгоритм: 1. находим 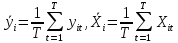 2. по полученным 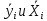 строим регрессию и находим остаточную дисперсию строим регрессию и находим остаточную дисперсию 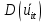 3. находим 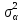 = =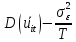 ( (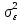 -остаточная дисперсия из модели с фиксированными эффектами) -остаточная дисперсия из модели с фиксированными эффектами)4. находим 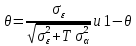 5. переходим к новым переменным 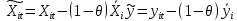 6. строим по ним регрессию и получаем оценки β – коэффициенты в модели со случайными эффектами. Для сравнения модели со случайными эффектами со сквозной регрессией (моделью пула) используется тест Бройша-Пагана. Это критерий для проверки в рамках RE-модели (со стандартными предположениями) гипотезы о равенстве межгрупповой дисперсии ошибок нулю: 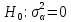 – сведение к модели пула. – сведение к модели пула.Статистика критерия Бройша–Пагана 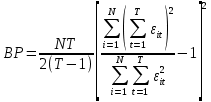 Здесь остатки берутся из модели пула. Статистика критерия Бройша–Пагана распределена по χ2(1). Соответственно, гипотеза H0 отвергается в пользу модели со случайными эффектами, если наблюдаемое значение статистики BP превышает критическое значение, рассчитанное по распределению χ2(1). Выбор между моделями с фиксированными или случайными эффектами Прежде всего напомним уже отмеченные ранее особенности моделей с фиксированными или случайными эффектами. • FE: получаемые выводы – условные по отношению к значениям эффектов αi в выборке; это соответствует ситуациям, в которых эти значения нельзя рассматривать как случайную выборку из некоторой более широкой совокупности (популяции). Такая интерпретация наиболее подходит для случаев, когда субъектами исследования являются страны, крупные компании или предприятия, т.е. каждый субъект ”имеет свое лицо”. • RE: получаемые выводы – безусловные относительно популяции всех эффектов αi. Исследователя интересуют не конкретные субъекты, а обезличенные субъекты, имеющие заданные характеристики. Для сравнения модели со случайными эффектами с моделью с фиксированными эффектами используется тест Хаусмана. Модель со случайным эффектом имеет место только в случае некоррелированности случайного эффекта с регрессорами. Это требование часто бывает нарушено. Как было показано Мундлаком, учет подобной корреляции приводит к регрессии, в которой МНК-оценки коэффициентов наклона совпадают с оценками «within». В тесте проверяются следующие гипотезы: 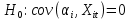 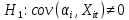 Можно проводить сразу несколько версий теста Хаусмана, введя 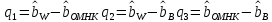 Для всех трех вариантов проверяется критерий 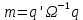 который распределен по χ2(k). Если остаемся в области Н0, следует пользоваться моделью RE со случайными эффектами. Если попадаем в критическую область, следует пользоваться моделью FE c фиксированными эффектами. |
