курсовая работа. Курсовая Хеда. Анализ поставленной задачи и постановка задачи на проектирование
 Скачать 59.57 Kb. Скачать 59.57 Kb.
|
СОДЕРЖАНИЕ
ВВЕДЕНИЕ Актуальность темы заключается в том, что сортировка данных на сегодняшний день при современном развитии компьютерных технологий является одним из наиболее распространенных процессов современной обработки данных. Задачи на сортировку данных встречаются очень часто в различных профессиональных сферах деятельности. Алгоритмы сортировки очень широко распространяются практически во всех задачах обработки информации. При этом они настолько тесно связаны друг с другом, что образуют отдельный класс алгоритмов. Алгоритмы сортировки, как правило, применяются с целью осуществления последующего более быстрого поиска. Например, трудно пользоваться словарями, если бы слова в них не были бы упорядочены по алфавиту. Важность сортировки основана на том факте, что на ее примере можно показать многие основные фундаментальные приемы и методы построения алгоритмов. Сортировка является хорошим примером огромного разнообразия алгоритмов, которые выполняют одну и ту же задачу. Кроме того, многие из них имеют определенные преимущества друг перед другом. За счет усложнения алгоритма можно добиться существенного увеличения эффективности и быстродействия алгоритма по сравнению с более простыми методами. Как правило, термин сортировка понимают, как процесс перестановки объектов некоторого множества в определенном порядке. Цель сортировки - облегчить последующий поиск элементов в отсортированном множестве. Алгоритмы информационного поиска и сортировки очень тесно связаны друг с другом. Они образовали фактически отдельный класс алгоритмов. Этот класс интересен и с точки зрения обучения, и с точки зрения использования при решении многих задач. Специфической особенностью данного класса является то, что внешне тривиальные задачи: «найти элемент» или «упорядочить последовательность элементов» допускают разнообразные решения. Цель курсовой работы заключается в изучении методов сортировки данных и применяемых алгоритмов поиска. Объектом исследования является алгоритмизация. Предметом исследования являются методы сортировки данных. Для достижения поставленной цели нужно решить следующие задачи: -изучить различные источники по выбранной теме; -исследовать различные методы и алгоритмы сортировки данных; -рассмотреть использование различных методов сортировки при поиске данных. -расширить, систематизировать и закрепление теоретические знания; -рассмотреть примеры использования методов сортировки данных. -провести сравнение различных методов сортировки. Практическая значимость работы может быть определена как приобретение навыков ведения самостоятельных теоретических и практических исследований в соответствии с направлением обучения в области поиска и сортировки данных, а также в формировании навыков правильного оформления научно-исследовательской работы. Теоретическое значение курсовой работы заключается в приобретении опыта обработки, анализа и систематизации результатов практических (экспериментальных) исследований. Курсовая работа состоит из введения, четырех разделов, списка используемой литературы. Работа содержит 3 рисунка и 5 таблиц. ГЛАВА 1. АНАЛИЗ ПОСТАВЛЕННОЙ ЗАДАЧИ И ПОСТАНОВКА ЗАДАЧИ НА ПРОЕКТИРОВАНИЕ1.1 Поиск, анализ и выбор основных вопросов, подлежащих реализации В соответствии с целями данного курсового проекта, возможно начать проектирование и анализ требуемых для проекта программ. В начале необходимо отметить основные типы и виды сортировок, их основные характеристики. Это необходимо для выделения основных отличий рассматриваемых в курсовом проекте сортировок от других существующих методов сортировок. По рекомендованной литературе выполнить теоретическое сравнение алгоритмов сортировок, рассматриваемых в рамках курсового проекта. Построить блок-схемы, наглядно отображающие принцип работы алгоритмов сортировок методом простых вставок и методом «пузырька». Далее следует описать, разработать и запрограммировать алгоритмы сортировки методом перестановки данных рассматриваемые в курсовом проекте. Протестировать программы (массивы должны сортироваться) и отобразить это в отчете. Выполнить сравнительный анализ работы двух алгоритмов сортировки, и выявить зависимость среднего времени сортировки от числа сортируемых элементов, построить график, отображающий данную зависимость. 1.2 Обзор алгоритма сортировки Сортировка - это процесс перестановки объектов данного множества в определённом порядке. Цель сортировки - облегчить последующий поиск элементов в отсортированном множестве. Поэтому элементы сортировки присутствуют во многих задачах прикладного программирования. Рассмотрим алгоритмы сортировки «на месте», то есть те алгоритмы в которых не используется копирование массива. Удобной мерой эффективности алгоритмов сортировки "на месте" является число необходимых сравнений в ходе сортировки и число необходимых пересылок элементов. Эффективные алгоритмы сортировки требуют порядка С=N*log2 (N) сравнений, где N - число элементов, а С - число необходимых сравнений. Мы рассмотрим простые методы сортировки, которые требуют число сравнений порядка. C=N2 Методы сортировки «на месте» можно разбить на три основных класса: -сортировка выбором -сортировка вставками -сортировка обменом В сортировке выбором выбирается элемент с наибольшим значением ключа и меняется местами с последним. Затем то же самое повторяется для s-1 элемента. Найденный элемент с наибольшим значением ключа меняется м 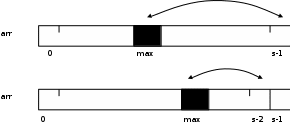 естами предпоследним элементом и т.д. (рисунок 1.1). Рисунок 1.1 Сортировка простым выбором В сортировке включениями элементы разделяются на уже упорядоченную и неупорядоченную последовательности. В начале упорядоченная часть содержит только один элемент. Очередной элемент из начала неупорядоченной части вставляется на подходящее место в упорядоченную часть. При этом упорядоченная часть удлиняется на один элемент, а неупорядоченная - укорачивается. Сортировка заканчивается при исчезновении неупорядоченной части (рисунок 2). 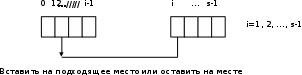 Рисунок 1.2 Сортировка простыми включениями Основная характеристика сортировки обменом - перестановка местами двух соседних элементов, если они расположены не так, как требует отсортированный массив.  Рисунок 1.3 Сортировка простым обменом В рассмотренной классификации существуют разные алгоритмы. Они отличаются сложностью, быстротой выполнения, последовательностью операций. Например: -сортировка вставками; -пузырьковая сортировка; -корневая сортировка; -пирамидальная сортировка; -сортировка слиянием; -быстрая сортировка; -сортировка Шелла и др. Рассмотрим подробнее основные типы и виды сортировок (сначала простые сортировки затем более сложные). -Сортировка массива простым выбором -Метод основан на следующем правиле: -Выбирается элемент с наибольшим значением ключа Он меняется местами с последним элементом arr [s-1]. Затем эти операции повторяются с оставшимися первыми s-1 элементами, затем - с s-2 первыми элементами и т.д. до тех пор, пока не останется только первый элемент - наименьший. Пример сортировки методом простого выбора показан на рисунке 1.4.   Рисунок 1.4 Сортировка массива простым выбором Эффективность сортировки простым выбором. Число сравнений ключей не зависит от начального порядка ключей. Операция сравнения выполняется в теле цикла с управляющей переменной kи средним числом повторений size/2. Этот цикл, в свою очередь, находится в теле цикла с управляющей переменной L и числом повторений size −1. Таким образом, число сравнений С= (size −1) * size −1/2 Число пересылок, напротив, зависит от начального порядка ключей. Если принять, что операция сравнения в теле цикла по k дает результат "истина" в половине случаев, то среднее число пересылок в этом цикле равно size/4. Цикл поL, как указывалось выше, выполняется size −1 раз и в теле цикла выполняется три пересылки и цикл по k. С учетом этого число пересылок: М= (3+ size/4) * (size −1) Получаем, что при сортировке простым выбором и число сравнений, и число пересылок пропорционально CIZE2. 1.3 Сортировка массива простыми включениями Метод простых вставок предполагает разделение всего массива элементов на упорядоченную часть, которая вначале содержит лишь один элемент, и неупорядоченную. Очередной элемент из неупорядоченной части вставляется в определенное место упорядоченной части, проходя сравнение с ее элементами. При поиске подходящего места удобно чередовать сравнения и пересылки, т.е. как бы "просеивать" выбранный элемент, сравнивая его с очередным элементом a [j] и либо вставляя, либо пересылая a [i] направо и продвигаясь налево. Заметим, что "просеивание" может закончиться при двух различных условиях: найден элемент a [j] с ключом меньшим, чем ключ x или достигнут левый конец готовой последовательности. При этом упорядоченная часть удлиняется на один элемент. Сортировка заканчивается при окончании неупорядоченной части. При данной сортировке общее число сравнений приблизительно равно С=N2 C=N*log2 (N) 4 При этом требуется количество проходов по данным P. P=log2 (N) Р 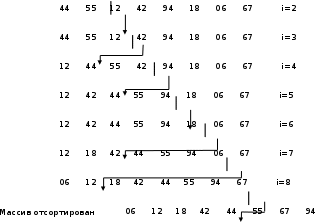 ассмотрим пошагово сортировку методом простых вставок на рисунке 1.5 Рисунок 1.5 Пример сортировки массива простыми включениями Число Ci сравнений ключей при i-м просеивании составляет самое большее i-1, самое меньшее 1 и, если предположить, что все перестановки n ключей равновероятны, в среднем равно i/2. Число Мi пересылок (присваиваний) равно Ci+2 (учитывая барьер). Поэтому общее число сравнений и пересылок есть Cmin = n-1 Mmin = 2 (n-1) Cср. = (n2+n-2) /4 Mср. = (n2+9n-10) /4 Cmax = ( (n2+n) - 1) /2 Mmax = (n2+3n-4) /2. Алгоритм сортировки простыми включениями можно легко улучшить, пользуясь тем, что готовая последовательность a [1],…, a [i-1], в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти значительно быстрее, применив бинарный поиск, который исследует средний элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения. ГЛАВА II. СОРТИРОВКА И АНАЛИЗ ЧИСЛОВЫХ МАССИВОВ-АЛГОРИТМОВ 2.1 Сортировка обменом, выбором, включением Понятие и теоретическая основа Пусть имеется некоторая последовательность однотипных записей, одно из полей записей выбрано в роли ключа, данное поле называется ключевым. Тип данных ключевого поля должен включать операции сравнения, то есть "=", ">", "<", ">=" и "<=". Тогда задача сортировки заключается в преобразовании исходной совокупности записей в такую последовательность записей, которая содержит те же записи, но в порядке убывания или возрастания значений ключевого поля. Метод сортировки будет называться устойчивым, если при его применении не изменяется относительное положение записей с равными значениями ключа. Экономия памяти – это главное требование, предъявляемое к методам сортировки. То есть, при выборе метода сортировки руководствуются критерием экономичного использования памяти. Классификация алгоритмов проводится в соответствии с эффективностью. Удобно измерять эффективность, подсчитывая число необходимых сравнений ключей и число пересылок элементов. Эти числа определяются некоторыми функциями от числа n сортируемых элементов. Исследование алгоритмов сортировки начинают с самых простых, но в то же время самых неэкономичных методов. Это объясняется следующими причинами: 1) Тексты программ, которые основаны на данных методах, легки и коротки для понимания. 2) Данные методы хорошо подходят для объяснения принципов и свойств сортировки. 3) Простая реализация позволяет экономить время работы программиста над разработкой программы, которое также необходимо учитывать, как составную часть при анализе эффективности работы программы. 4) При достаточно малой размерности массивов эти методы часто работают даже лучше, чем более сложные методы. Методы внутренней сортировки можно разбить на три основных группы. Они классифицируются в зависимости от лежащего в их основе метода: 1) Сортировка обменом. 2) Сортировка выбором. 3) Сортировка включением. Самым распространенным алгоритмом сортировки является пузырьковый способ (или способ сортировки обменом). Данный метод основан на выполнении в цикле операций сравнения и при необходимости обмена смежных элементов. Название алгоритма дано ему из-за аналогии с процессом всплывания пузырьков в сосуде с водой. То есть, каждый пузырек всплывает до своего собственного уровня, определяемого соответствующим весом «пузырька». Другими словами, идея метода сортировки пузырьком заключается в сравнении смежных элементов и их обмене, если они находятся не в нужном порядке. Повторное выполнение таких действий заставляем наименьший элемент "всплывать" в начало последовательности. Следующий проход приведет к всплыванию второго наименьшего элемента массива, и так до тех пор, пока после итерации список не будет полностью отсортирован. Таким образом, массив данных будет отсортирован по возрастанию. Для сортировки последовательности элементов по возрастанию, сначала всплывает наибольший элемент в начало последовательности. При следующем проходе второй по величине элемент всплывает и тд. Далее приведен фрагмент программы, реализующий поиск пузырьком на языке Паскаль: -for i:=n-1 downto 1 do {n – количество элементов в массиве} -for j:=1 to i do -if a[j]>a[j+1] then -begin -y:= a[j]; -a[j]:= a[j+1]; -a[j+1]:= y; -end; Данный алгоритм основан на двух вложенных циклах. Так как число элементов массива задается переменнойn, внешний цикл вызывает просмотр массива раз. В результате этой процедуры каждый элемент встает на искомую позицию. Внутренний цикл фактически выполняет операции сравнения и обмена. Пример процесса сортировки обменом представлен в таблице 1. Для иллюстрации работы сортировки пузырьковым методом в таблице 1 даны результаты каждого этапа сортировки массива.
Таблица 1. Сортировка массива методом пузырька Сортировка большого числа элементов данным методом потребует большого времени, поскольку время выполнения сортировки квадратично зависит от числа элементов последовательности. Сортировка в этом случае осуществляется выбором элемента массива с наименьшим значением и обменом его с первым элементом последовательности. Далее находится элемент с наименьшим значением из оставшихся элементов и делается его обмен со вторым элементом до обмена двух последних элементов. В общем случае, при i-ом проходе по массиву (0 i n– 2) алгоритм ищет наименьший элемент среди последних n – i элементов и обменивает его с a[i]; После выполнения n – 1 проходов список оказывается отсортирован. Кол программы на языке Паскаль, которая реализует данный алгоритм: for i = 0 to n – 2 do min = I; for j = i + 1 to n – 1 do if a[j] < a[min] then begin min = j y:= a[i]; a[i]:= a[min]; a[min]:= y; end; Для иллюстрации работы сортировки пузырьковым методом в таблице 2 представлены результаты каждого этапа сортировки массива.
Таблица 2. Сортировка выбором Данная сортировка является последней из простых алгоритмов. При сортировке включением (вставками) сначала упорядочиваются первые два элемента последовательности. Затем последовательно осуществляется вставка третьего элемента массива в соответствующую для него позицию по отношению к первым двум элементам, а затем четвертый элемент вставляется в список из трех элементов. Этот процесс повторяется до тех пор, пока весь массив не будет отсортирован. Таким образом, процесс сортировки вставками осуществляется путем сканирования, отсортированного подмассива слева направо, пока не достигается первый элемент, больший или равный a[n–1], и после этого происходит вставка элемента непосредственно перед найденным элементом. Сортировка включением (вставками) основана на рекурсии. Однако более эффективной будет ее итеративная реализация, то есть снизу вверх. Элемент a[i] (начиная с элемента a[1] и заканчивая a[n–1]) вставляется на соответствующую позицию среди первых i элементов массива, которые к этому времени уже отсортированы. Однако в отличие от сортировки выбором элемент в общем случае вставляется не в окончательную позицию, которую он будет занимать в полностью отсортированном массиве [2, с. 230]. Ниже приведен фрагмент программы на языке Паскаль, которая реализует сортировку включением. -for i = 1 to n - 1 do -y= a[i]; -j = i – 1; -while j >= 0 and a[j] >y do begin -mass[j + 1] = a[j]; -j = j – 1; -end; -a[j + 1] = y; Иллюстрация работы алгоритма представлена в таблице 3.
Таблица 3. Сортировка вставками Сортировка простыми вставками противоположна сортировке простым выбором. При сортировке простыми вставками (включениями) на каждом шаге алгоритма рассматривается только один очередной элемент входного массива и все элементы готового массива для нахождения места вставки. Сортировка вставками имеет два преимущества: 1) Данный метод обладает естественным поведением. Другими словами, сортировка включением выполняется быстрее для упорядоченного массива и дольше всего выполняется, когда массив упорядочен в обратном направлении. Это полезно в том случае, когда массив почти отсортирован. 2) Сортировка включением устойчива. Элементы с одинаковыми ключами не переставляются, и если список элементов сортируется с использованием двух ключей, то после завершения сортировки вставками он по-прежнему будет отсортирован по двум ключам. Хотя число сравнений может быть достаточно небольшим для определенных последовательностей элементов, постоянные сдвиги массива требуют выполнения большого числа операций перестановок. 2.2 Сравнение и рассмотрение способов внутренней и внешней сортировки Анализируя любой метод сортировки, можно получить число операций сравнения и обмена, выполняемых в лучшем, среднем и худших случаях. Для рассмотренных методов внутренней сортировки существуют точные формулы, вычисление которых дает минимальное, максимальное и среднее число сравнений ключей (C) и пересылок элементов массива (M). [2] Таблица 4 содержит данные, приводимые в книге Никласа Вирта
Таблица 4. Сравнение методов внутренней сортировки Прямое слияние Внешней сортировкой называется сортировка последовательных файлов, которые располагаются во внешней памяти. Данные файлы слишком велики, чтобы полностью поместиться в основную память, поэтому к ним неприменимы рассмотренные ранее методы внутренней сортировки. Чаще всего внешнюю сортировку используют в системах управления базами данных. Пусть имеется некоторый последовательный файл А, который включает в себя записи а1, а2,…, аn. Каждая такая запись состоит из одного ключевого элемента. Для сортировки прямым слиянием необходимы два вспомогательных файла В и С, размер каждого из них равен n/2. В таблице 5 показан пример внешней сортировки простым слиянием.
Таблица 5. Внешняя сортировка простым слиянием Данный метод сортировки состоит из последовательных шагов. На каждом таком шаге выполняется распределение файла А в файлы В и С, а затем осуществляется слияние файлов В и С в исходный файл А. Файл А содержит записи: 8 23 5 95 44 33 2 6. Размер файла А=8, таким образом, размер вспомогательных файлов В и С равен n/2=4. Сначала осуществляется начальное распределение: последовательно считываются записи файла А, записи a1, a3, ..., a(n-1) пишутся в файл B, а записи a2, a4, ..., an - в файл C. То есть файл В содержит элементы: 8 5 44 2, а файл С: 23 95 33 6. На втором шаге снова осуществляется последовательное считывание файла А, при этом в файл В записываются последовательные пары с нечетными номерами, а в файл С – с четными. В процессе слияния образуются упорядоченные четверки записей. Они записываются в файл А. И так продолжается до последнего шага. Перед последним шагом, файл А будет содержать две упорядоченные подпоследовательности размером n/2 каждая. В процессе очередного распределения первая из них попадает в вспомогательный файл В, а вторая в С. В результате слияния исходный файл А будет содержать полностью упорядоченную последовательность записей. Естественное слияние Недостатком предыдущего способа можно считать то, что при прямом слияние не рассматривается то факт, что исходный файл может быть уже частично отсортирован. Устранить данный недостаток призван метод естественного слияния. При этом методе сортировка выполняется за несколько шагов, как и при методе прямого слияния. На каждом шаге сначала выполняется распределение исходного файла А по вспомогательным В и С, а потом слияние вспомогательных в исходный файл. При распределении распознается первая серия записей и переписывается в файл B, вторая - в файл C и т.д. В процессе слияние осуществляется сливание первой серии файла В с первой серией файла С, второй серии файла В со второй серией С и т.д. В случае, если по причине разного размера серий, просмотр одного файла закончился раньше, чем просмотр другого, то остаток большего файла записывается в конец исходного файла целиком. Процесс сортировки методом естественного слияния заканчивается, когда в исходном файле А остается одна серия. Пример данной сортировки представлен на рисунках 1 и 2.
Рисунок 1. Первый шаг сортировки
       
Рисунок 2. Второй шаг сортировки При использовании метода естественного слияния число чтений и записи файлов будет меньше, чем при использовании метода прямого слияния. Но с другой стороны увеличивается число сравнений, это обуславливается распознаванием концов серий. Кроме того, поскольку длина серий может быть произвольной, то максимальный размер файлов B и C может быть близок к размеру файла A. Сбалансированное многопутевое слияние В основе сбалансированного многопутевого слияния лежит распределение серий исходного файла по нескольким вспомогательным, то есть по по m вспомогательным файлам B1, B2, ..., Bm и их слияние в m вспомогательных файлов C1, C2, ..., Cm. На следующем шаге производится слияние файлов C1, C2, ..., Cm в файлы B1, B2, ..., Bm и т.д., пока в B1 или C1 не образуется одна серия. Сбалансированное многопутевое слияние является развитием идеи двухпутевого слияния, использованного в предыдущих методах сортировки. Простой пример использования данного метода представлен на рисунке 3.
Рисунок 3. Многопутевое слияние Данный метод сортировки имеет следующие преимущества: число проходов алгоритма оценивается как O(log n) (n - число записей в исходном файле), где логарифм берется по основанию n. Порядок числа копирований записей равен O(log n). Но число сравнений не будет меньше, чем при использовании метода простого слияния. Таким образом, чем более длинные серии содержит файл перед началом применения внешней сортировки, тем меньше потребуется слияний и тем быстрее закончится сортировка. Поэтому до начала применения любого из методов внешней сортировки, основанных на применении серий, начальный файл частями считывается в основную память, к каждой части применяется один из наиболее эффективных алгоритмов внутренней сортировки. Кроме того, конечно, при выполнении распределений и слияний используется буферизация блоков файла(ов) в основной памяти. Возможный выигрыш в производительности зависит от наличия достаточного числа буферов достаточного размера. ЗАКЛЮЧЕНИЕ Алгоритмы сортировки числовых массивов применяется во всех без исключения областях программирования, будь то базы данных или математические программы. Алгоритмы сортировки представляют собой пошаговое упорядочение элементов в определенном массиве данных, независимо от его размеров. Практически каждый алгоритм сортировки можно разбить на три части: сравнение, определяющее упорядоченность пары элементов; перестановку, меняющую местами пару элементов; собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены. Важность сортировки основана на том факте, что на ее примере можно показать многие основные фундаментальные приемы и методы построения алгоритмов. Сортировка является хорошим примером огромного разнообразия алгоритмов, которые выполняют одну и ту же задачу. Кроме того, многие из них имеют определенные преимущества друг перед другом. За счет усложнения алгоритма можно добиться существенного увеличения эффективности и быстродействия алгоритма по сравнению с более простыми методами. Как правило, термин сортировка понимают, как процесс перестановки объектов некоторого множества в определенном порядке. Цель сортировки - облегчить последующий поиск элементов в отсортированном множестве. Различают методы внутренней и внешней сортировки. К методу внутренней сортировки относят методы сортировки массив. Методы сортировки массивов можно разделить на три основных класса в зависимости от лежащего в их основе метода: сортировка пузырьком; сортировка выбором; сортировка включением. Пузырьковая сортировка просто реализуется, но используется только в учебных целях и не используется на практике. Это объясняется тем, что сортировка обменом эффективна лишь при небольших массивах элементов. Сортировка выбором так же относится к простым методам сортировки. И, как и при методе пузырька, данная сортировка выполняется слишком медленно для большого числа элементов. Однако хотя, для сортировок пузырьковым методом и сортировок выбором, число операций обмена для среднего случая будет значительно меньшим для сортировки выбором. Сортировка вставками является последней из простых алгоритмов. В отличие от сортировки методом обмена и сортировки выбором, количество операций сравнения для сортировки вставками зависит от исходной упорядоченности массива элементов. Сортировка включением имеет естественное поведение и требует наименьшее число операций обмена для почти упорядоченного списка, а также наибольшее число операций обмена, в тех случаях, когда массив данных упорядочен в противоположном направлении. Время выполнения простых сортировок пропорционально квадрату числа элементов в массиве. Способы внешней сортировки используются, когда исходный файл, содержащий записи, не может быть полностью помещен в основную память. Существуют следующие методы внешней сортировки: метод прямого слияния, метод естественного слияния, метод сбалансированного многопутевого слияния. Чем более длинные серии содержит файл перед началом применения внешней сортировки, тем меньше потребуется слияний и тем быстрее закончится сортировка. Поэтому до начала применения любого из методов внешней сортировки, основанных на применении серий, начальный файл частями считывается в основную память, к каждой части применяется один из наиболее эффективных алгоритмов внутренней сортировки. В ходе выполнения курсовой работы рассмотрены этапы эволюции методов сортировки данных, выполнен сравнительный анализ и изучены основные методы сортировки данных. Получены навыки ведения самостоятельных теоретических и практических исследований и навыки правильного оформления научно-исследовательской работы. Также приобретен опыт обработки, анализа и систематизации результатов практических исследований по направлению обучения. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ Алексеев Е.Р., Чеснокова О.В., Кучер Т.В., Самоучитель по программированию на Free Pascal и Lazarus. - Донецк.: ДонНТУ, Технопарк ДонНТУ УНИТЕХ, 2013. – 503 с. Вирт Н. Алгоритмы и структуры данных. М.: Мир, 2014. - 360 с. Гагарина Л.Г., Алгоритмы и структуры данных: Учебное пособие. – М.: ИНФРА-М, 2013. – 304 с.: ил, ISBN 978-5-16-003-682-3. Гагарина Л.Г., Алгоритмы и структуры данных: Учебное пособие. – М.: ИНФРА-М, 2012. – 304 с.: ил, ISBN 978-5-16-003-682-3. Демидов Д.В., Основы программирования на языке Pascal в примерах: Учебное пособие. – М.: НИЯУ МИФИ, 2016. – 172 с. Демидов Д.В., Основы программирования на языке Pascal в примерах: Учебное пособие. – М.: НИЯУ МИФИ, 2011. – 172 с. Дупленко А. Г. Сравнительный анализ алгоритмов сортировки данных в массивах // Молодой ученый. — 2013. — № 8. — 80 с. Кауфман В.Ш. Языки программирования. Концепции и принципы. – М.: ДЖК Пресс, 2014. – 464 с. Красиков И.В. Алгоритмы. Просто как дважды два. – М.: Эксмо, 2013. – 256 с. ISBN 978-5-699-21047-3. Кулаков В.Г., Алгоритмический язык Паскаль: Учебное пособие. – М.: МГИЭМ, 2014. – 41 с. Лозовая С.Ю., Решение типовых задач по программированию: практическое пособие: НИУ БелГУ; НИУ БелГУ.-Белгород: ИПК НИУ "БелГУ", 2011. - 148 с. Марапулец Ю.В., Программирование на языках высокого уровня: Учебное пособие. – КамчатГТУ, 2014. – 189 с. ISBN 978-5-328-00185-4. Павловская Т.А. Паскаль. Программирование на языке высокого уровня: Учебник для вузов. – СПб.: Питер, 2012. – 393с. Павловская Т.А., Паскаль. Программирование на языке высокого уровня: Учебник для вузов. – СПб.: Питер, 2015. – 464с. Попов И.И., Основы алгоритмизации и программирования: Учебное пособие. – 3-е издание – М.: Форум, 2014. – 432 с. Потопахин В.В. Искусство алгоритмизации: Учебное пособие. – М.: ДЖК Пресс, 2014. – 320 с., ил., ISBN 978-5-94074-621-8. Потопахин В.В., Искусство алгоритмизации: Учебное пособие. – М.: ДЖК Пресс, 2015. – 320 с., ил., ISBN 978-5-94074-621-8. Потопахин В.В., Современное программирование с нуля. – М.: ДЖК Пресс, 2010. – 240 с., ил. Решение 50 типовых задач по программированию на языке Pascal – 2012 [Электронный ресурс] – URL: http://el-prog.narod2.ru/ (дата обращения: 12.09.2022). Сулейманов Р.Р., Методика решения учебных задач средствами программирования: Методическое пособие – М: БИНОМ. Лаборатория знаний 2014, с. 112, ISBN:978-5-9963-0112-6. Язык Pascal. Программирование для начинающих. – 2011 [Электронный ресурс] - URL: http://pas1.ru/pascaltextbook (дата обращения: 12.09.2022). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 5
5