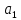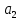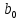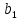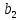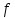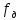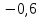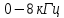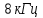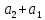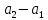цос 2.6-2. Анализ рекурсивных цифровых фильтров 1го и 2го порядка
 Скачать 235.76 Kb. Скачать 235.76 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Государственное образовательное учреждение высшего профессионального образования _______________________________________________ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ Кафедра общей теории связи ЛАБОРАТОРНАЯ РАБОТА № 26-2 по дисциплине «Цифровая обработка сигналов» на тему: «Анализ рекурсивных цифровых фильтров 1-го и 2-го порядка» Вариант №2 Выполнил: студ. гр. БМС1301 Дарьин Роман Проверил: проф. каф. ОТС Волчков В. П. (Осенний семестр) Москва 2015 1. Цель работы На персональном компьютере провести анализ рекурсивных цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики фильтров, а так же их взаимосвязь со значениями коэффициентов (параметров) ЦФ; определить области устойчивости рекурсивных фильтров 1 и 2 порядка. 2. Выполнение домашнего задания 2.1. Исходные данные варианта Исходные данные в соответствии с номером варианта представлены в табл. 1.
Табл. 1. Таблица значений параметров фильтра. 2.2. Запись разностного уравнения и системной функции ЦФ 1-го порядка Разностное уравнение в общем виде: 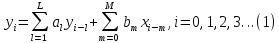 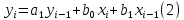 Подставим в уравнение значения коэффициентов и получим итоговое разностное уравнение: 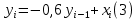 После получения разностного уравнения можем составить системную функцию. Системная функция в общем виде: 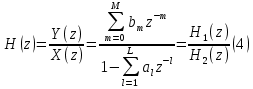 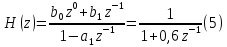 2.3. Изображение структурной схемы ЦФ. Построим структурную схему ЦФ 1-го порядка с заданными коэффициентами. 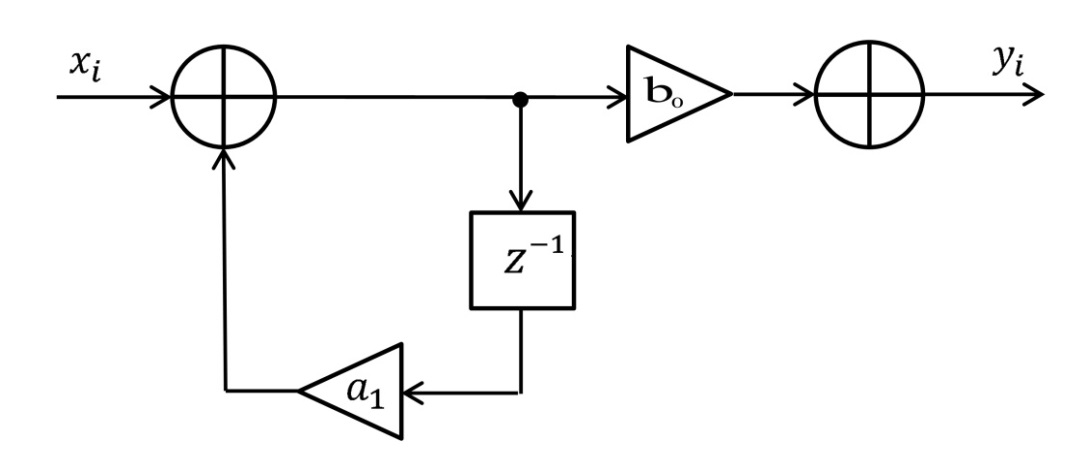 Рис. 1. Структурная схема рекурсивного ЦФ 1-го порядка ( 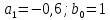 ) )2.4. Расчёт импульсной реакции и амплитудно-частотной характеристики ЦФ Импульсной реакцией 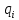 ,i = 0, 1, 2, …, называется отклик ЦФ на входной единичный импульс: ,i = 0, 1, 2, …, называется отклик ЦФ на входной единичный импульс: 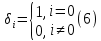 В соответствии с формулами (3) и (6) получаем импульсную реакцию заданного рекурсивного ЦФ 1-го порядка: 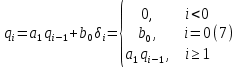 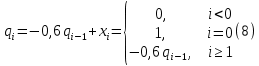 Теперь построим график импульсной характеристики по полученным точкам. 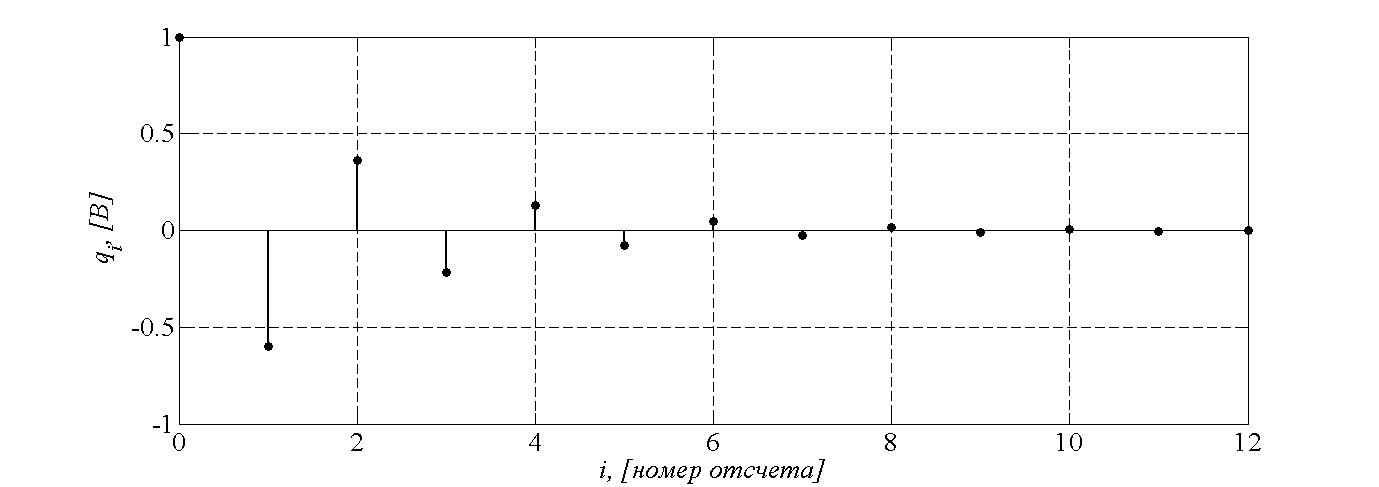 Рис. 2. Импульсная реакция рекурсивного ЦФ 1-го порядка ( 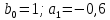 ) )Передаточная и системная функции ЦФ связаны равенством: 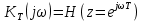 . При определении АЧХ и ФЧХ ЦФ его передаточную функцию нужно представить в следующем виде: . При определении АЧХ и ФЧХ ЦФ его передаточную функцию нужно представить в следующем виде: 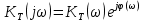 . Здесь . Здесь 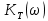 является модулем функции является модулем функции 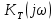 или АЧХ, а или АЧХ, а 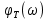 – аргумент функции – аргумент функции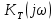 или ФЧХ ЦФ. Тогда, при подстановке или ФЧХ ЦФ. Тогда, при подстановке 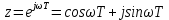 в найденную нами в пункте 2.2. системную функцию, мы получим уравнение вида: в найденную нами в пункте 2.2. системную функцию, мы получим уравнение вида: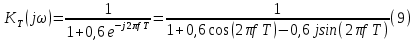 Отсюда мы можем найти АЧХ ЦФ, которую можно найти по формуле: 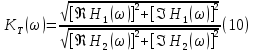 АЧХ примет вид: 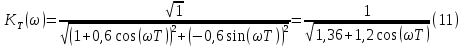 По условию, нам задан диапазон от 0 до 8 кГц, значит, частота дискретизации 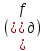 равна 8 кГц. Тогда мы можем найти период по формуле: равна 8 кГц. Тогда мы можем найти период по формуле: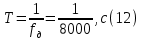 Зная период, мы можем вычислить и построить график АЧХ: 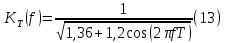 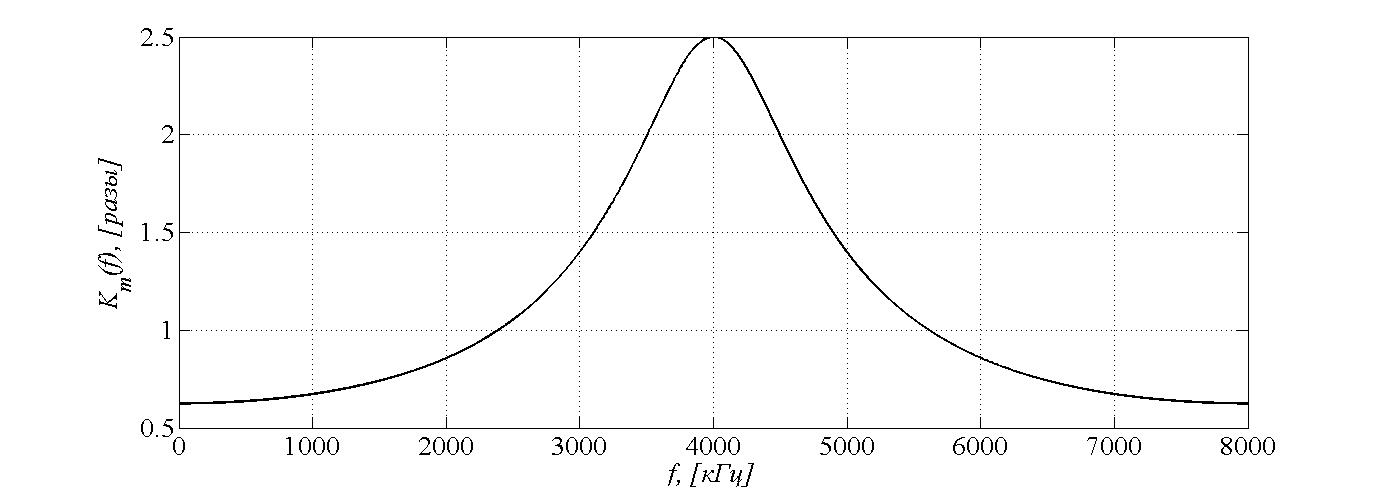 Рис. 3. АЧХ рекурсивного ЦФ 1-го порядка ( 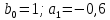 ) )Выполнение лабораторной работы Исходные параметры фильтров
Структурная схема ЦФ 2-го порядка Структурная схема исследуемого рекурсивного ЦФ второго порядка представлена ниже 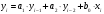 (14) (14)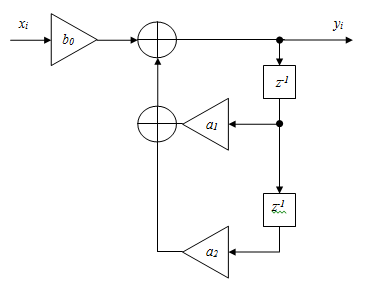 Рис. 4. Неканоническая структурная схема рекурсивного ЦФ 2-го порядка. Для построения канонической структурной схемы введем вспомогательную функцию: 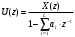 (15) (15)Откуда получаем следующее соотношение U(z): 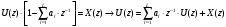 (16) (16)Изображение отклика ЦФ имеем: 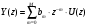 (17) (17)Применяя обратное Z-преобразование и используя свойства Z-преобразования, приходим к соотношениям для последовательностей {ui} и {yi} : 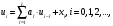 (18) (18)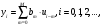 (19) (19)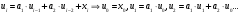 (20) (20)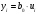 (21) (21)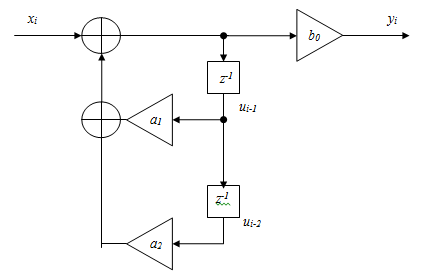 Рис. 5. Каноническая структурная схема рекурсивного ЦФ 2-го порядка. Результаты эксперимента В данном отчете приведены импульсные характеристики (ИХ), амплитудно-частотные характеристики (АЧХ), переходные характеристики (ПХ), которые рассчитываются по данным формулам: ИХ фильтра первого порядка: 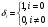 (22) (22)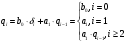 (23) (23)ИХ фильтра второго порядка: 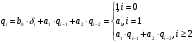 (24) (24)АЧХ фильтра первого порядка: 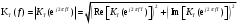 (25) (25)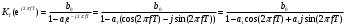 (16) (16)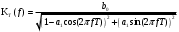 (26) (26)АЧХ фильтра второго порядка: 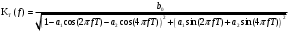 (27) (27)ПХ фильтров: 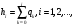 (28) (28)Детальные выводы по проделанной работе. Устойчивость: Фильтры № 3а и № 6а являются неустойчивыми, это мы можем доказать с помощью трех неравенств устойчивости: 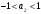 (29) (29)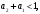 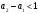 (30) (30)Поскольку фильтр №3 имеет значение коэффициента 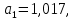 а фильтр №6 имеет значение коэффициента а фильтр №6 имеет значение коэффициента 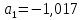 , мы можем сделать вывод, что они не устойчивы, так как условие (30) не выполняется. , мы можем сделать вывод, что они не устойчивы, так как условие (30) не выполняется.Все остальные фильтры устойчивы, так как удовлетворяют заданным условиям.
2) Классификация исследуемых фильтров: ФНЧ–в фильтре нижних частот АЧХ локализована в обрасти нижних частот. ФВЧ – в фильтре верхних частот АЧХ локализована в области частоты Найквиста. ПФ– в полосовом фильтре АЧХ локализована в области между 0 и частотой Найквиста. В домашней работе, рекурсивный ЦФ 1-го порядка (b0 = 1, a1 = -0,6) представляет собой фильтр верхних частот (ФВЧ). Список номеров фильтров и соответствующих им типов, полученных в результате анализа частотных характеристик:
3) Сравнение АЧХ рекурсивных ЦФ и нерекурсивных ЦФ 1-го и 2-го порядка: Сравнение ФВЧ (АЧХ-№2, №5, №6 из лаб. 26-1 и АЧХ-№2a, №4a, №6а, №8а, №2б из лаб. 26-2) для одного и того же порядка, можно сделать вывод, что: Рекурсивные фильтры имеют более крутой подъем АЧХ на границе полосы пропускания; ЦФ 2-го порядка имеют нежелательные пульсации, как нерекурсивные (АЧХ-№5 из лаб. 26-1), так и рекурсивные (АЧХ-№2б из лаб. 26-2). Однако можно заметить, что в рекурсивных ЦФ пульсации менее заметны. Сравнение ФНЧ (АЧХ-№1, №3, №4 из лаб. 26-1 и АЧХ-№1a, №3a, №5а, №7а, №1б из лаб. 26-2) для одного и того же порядка, можно сделать вывод, что: Рекурсивные фильтры имеют более крутой спад АЧХ на границе полосы пропускания; ЦФ 2-го порядка имеют нежелательные пульсации, как нерекурсивные (АЧХ-№5 из лаб. 26-1), так и рекурсивные (АЧХ-№2б из лаб. 26-2). Однако можно заметить, что в рекурсивных ЦФ пульсации менее заметны. 4) Сравнение АЧХ рекурсивных ЦФ 1-го и 2-го порядка: Сравнив АЧХ-№4а и №2б ФВЧ разных порядков можно сделать вывод: Чем больше порядок, тем больше крутизна подъема; В фильтре 2-го порядка наблюдаются нежелательные пульсации в полосе пропускания. Сравнив АЧХ-№5а и №1б ФНЧ разных порядков можно сделать вывод: Чем больше порядок, тем больше крутизна спада; В фильтре 2-го порядка наблюдаются нежелательные пульсации в полосе задерживания. 5) Преимущества и недостатки БИХ-фильтров: Преимущества: БИХ фильтры могут быть использованы для реализации цифровых аналогов классических видов аналоговых фильтров, таких как фильтры Баттерворта, Чебышева и т.д. При аналогичных характеристиках, БИХ фильтры имеют более простую реализацию по сравнению с КИХ фильтрами. Недостатки: БИХ фильтры более чувствительны к конечной разрядности вычислений, которая приводит к появлению колебаний т.н. «предельных циклов». За исключением специального случая, когда все полюса передаточной функции лежат на единичной окружности z-плоскости, невозможно построить реализуемый стабильный БИХ фильтр, имеющий точно линейную ФЧХ. |