Анализ вычислительной сложности алгоритма сортировки массива методом Шелла. Анализ вычислительной сложности алгоритма сортировки массива ме. Анализ вычислительной сложности алгоритма сортировки массива методом Шелла Постановка задачи

• Название: Анализ вычислительной сложности алгоритма сортировки массива методом Шелла Постановка задачи
• Анкор: Анализ вычислительной сложности алгоритма сортировки массива методом Шелла
• Дата: 07.11.2021
• Размер: 0.79 Mb.
• Имя файла: Анализ вычислительной сложности алгоритма сортировки массива ме.docx
• Тип: Анализ; #265411

Анализ вычислительной сложности алгоритма сортировки массива методом Шелла

Постановка задачи

Составить программу сортировки массива методом Шелла.

В программе должны быть предусмотрены два варианта формирования исходного массива (выбирается в начале работы программы):

• 
  вводом с клавиатуры (для тестового прогона программы), n=10;
  
• 
  с помощью генератора псевдослучайных чисел (для рабочего прогона программы), n=1000, 10000, 100000, 1000000.
  

Провести аналитическую и практическую оценки вычислительной сложности алгоритма. Примечание:

- Практическая оценка вычислительной сложности алгоритма производится путем вычисления количества выполненных операций сравнения С и перемещения М.

Описание алгоритма

Сортировка Шелла (англ. Shell sort) — алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Изобретатель этого метода Дональд Шелл опубликовал этот алгоритм в 1959 году. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и на определённом расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными «грубыми» проходами. При сортировке Шелла сначала сравниваются и сортируются между собой значения, стоящие один от другого на некотором расстоянии d (по-другому называется шаг). После этого процедура повторяется для некоторых меньших значений d, а завершается сортировка Шелла упорядочиванием элементов при d=1 (то есть обычной сортировкой вставками).

Текст исходного кода программы

Алгоритм реализован на языке программирования Python.

import random

max_array_size_for_manual_input = 10
limit_of_show_progress = 100
random_from = 1
random_to = 10000

n = int(input('Please enter array size: '))
is_generate_random_values = n > max_array_size_for_manual_input

arr = []
for i in range(n):
if n <= max_array_size_for_manual_input:
arr.insert(i, int(input('Enter ' + str(i) + ' item value: ')))
else:
random.seed()
arr.insert(i, random.randint(random_from, random_to))

is_show_progress = bool(input('Show progress (0/1)?: '))

count_of_compare = 0
count_of_move = 0

gap = n // 2
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap:
count_of_compare += 1
if arr[j - gap] > temp:
count_of_move += 1
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
else:
break
if is_show_progress and n < limit_of_show_progress:
print(arr)
gap //= 2
if n < limit_of_show_progress:
print(arr)
print('Count of compare: ' + str(count_of_compare))
print('Count of move: ' + str(count_of_move))
Контрольные прогоны программы
Тест №1 - n = 10:

Тест №2 - n = 1000: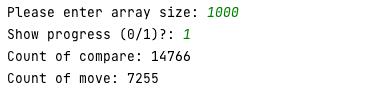

Тест №3 - n = 10 000: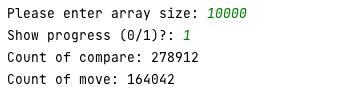


Тест №4 - n = 100 000: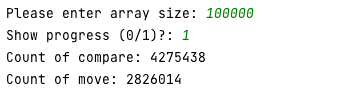


Тест №5 - n = 1000 000: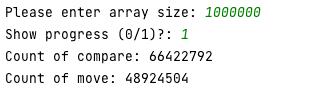

Результаты.

Размер массива (n)	Практическая сложность	Теоретическая сложность (худший случай)
10	42	100
1 000	22 021	1 000 000
10 000	442 954	100 000 000
100 000	7 101 452	10 000 000 000
1 000 000	115 347 296	1 000 000 000 000

Особенность сортировки Шелла состоит в том, что элементы «быстрее» встают на свои места. Эффективность этого алгоритма объясняется тем, что на каждом шаге просматривается относительно небольшое количество элементов. Кроме того, что принципиально, элементы массива уже частично отсортированы и их упорядоченность увеличивается при каждом новом проходе массива. Кроме того, сортировка методом Шелла наиболее эффективна, когда массив уже частично отсортирован.