юд. вар 1 лаб работа 3. Аппроксимация первой и второй производных через конечные разности

• Название: Аппроксимация первой и второй производных через конечные разности
• Дата: 01.10.2022
• Размер: 52.07 Kb.
• Имя файла: вар 1 лаб работа 3.docx
• Тип: Документы; #708717

Аппроксимация первой и второй производных

через конечные разности

Вспомним определение первой производной. Если f (x) – функция одной переменной и x₀ ∈ [a, b], то функцию f ′(x) можно записать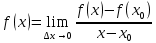

, (1)

где x₀ – фиксированная точка.

Геометрическая интерпретация показана на рис. 1. Пусть на графике функции f заданы фиксированная точка P₀ [x₀, f (x₀)] и подвижная точка P [x, f(x)], и секущая, проведенная через эти точки, образует угол β с положительным направлением оси x.

, (2)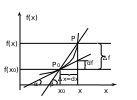



Рис. 1. Геометрическая интерпретация первой производной

Разностное отношение функции f в точке x₀ равно угловому коэффициенту секущей, проведенной через точки P и P₀. Функция f называется дифференцируемой в точке x₀∈[a,b], если существует предел разностного отношения функции в точке x₀:

, (3)

Предел (3) называется производной функции f в точке x₀ и обозначается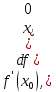

(4)

Производная функции f в точке x₀ – это тангенс угла наклона касательной к графику функции f в точке P₀[x₀, f(x₀)](рис. 1)

tgα= f ′(x₀ )`. (5)

Простейшая формула численного (приближенного) дифференцирования для непрерывной функции в точке x₀ через конечные разности имеет вид

f ′(x0) = f x( 0 + ∆x) − f x( 0)(6)

∆x

или f ′(x0) = f x( 0 + ∆x) − f x( 0 − ∆x) ,

2⋅∆x

где ∆x=x₁– x₀или в общем виде ∆x=x_i – x_i-1– шаг дифференцирования, величина которого должна быть достаточно малой.

Если производная функции f ^/ (4) дифференцируема в точке то [f ′( )_x ]′ называется второй производной функции f в

x₀,

x x= ₀

точке x₀ и обозначается одним из приведенных способов

′′(x₀),d² f x(2 ₀) ,d²2f . (7)

f

dx dx

x x= ₀

Формула численного нахождения второй производной

f ′′(x0) = f ′(x0 + ∆x) − f ′(x0)(8)

∆x

При подстановке в (8) выражения для нахождения первой производной получим

f ′′(x0) = f x( 0 + 2⋅∆x) − 2⋅ f x2( 0 + ∆x) + f x( 0)(9)∆x

45

или f ′′(x0) = f x( 0 + ∆x) − 2⋅ f x(2 0) + f x( 0 − ∆x) .

∆x

При численном дифференцировании исходят из того, что функция f (x) задана конечной последовательностью пар значений (x_i , f_i) без помехи, и приближенные значения величин f ^/ _(xi ) и f ^// (x_i ) находят по формулам (6) и (9).