Главная страница
Навигация по странице:

  • 22. B 4 № 137310.

  • 30. B 4 № 311757.

  • 32. B 4 № 311845.

  • 36. B 4 № 314408.

  • 38. B 4 № 314425.

  • 44. B 4 № 314632.

  • 48. B 4 № 314653.

  • 50. B 4 № 316254.

  • 52. B 4 № 316317.

    		•

    Арифметические и геометрические прогрессии b 4 35


    Скачать 241 Kb.
    НазваниеАрифметические и геометрические прогрессии b 4 35
    Дата29.03.2022
    Размер241 Kb.
    Формат файлаdoc
    Имя файла6Arif_GeometrProgressia.doc
    ТипДокументы
    #426772

    Ариф­ме­ти­че­ские и гео­мет­ри­че­ские прогрессии

    1. B 4 № 35. Дана ариф­ме­ти­че­ская про­грес­сия: Най­ди­те сумму пер­вых де­ся­ти её чле­нов.

    Ответ: 50
    2. B 4 № 87. Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­я­ми: . Най­ди­те  

    Ответ: 256
    3. B 4 № 113. Дана ариф­ме­ти­че­ская про­грес­сия   Най­ди­те   .

    Ответ: 23
    4. B 4 № 139. Дана ариф­ме­ти­че­ская про­грес­сия   Най­ди­те сумму пер­вых де­ся­ти её чле­нов.

    Ответ: 75
    5. B 4 № 191. Ариф­ме­ти­че­ская про­грес­сия за­да­на усло­ви­я­ми:  . Най­ди­те

    Ответ: 32
    6. B 4 № 137294. По­сле­до­ва­тель­ность за­да­на фор­му­лой . Какое из ука­зан­ных чисел яв­ля­ет­ся чле­ном этой по­сле­до­ва­тель­но­сти?

     

    1) 1
    2) 2
    3) 3
    4) 4

    Ответ: 3
    7. B 4 № 137295. По­сле­до­ва­тель­ность за­да­на фор­му­лой . Какое из сле­ду­ю­щих чисел не яв­ля­ет­ся чле­ном этой по­сле­до­ва­тель­но­сти?

     

    1)

    2)

    3)

    4)

    Ответ: 3
    8. B 4 № 137296. Какое из ука­зан­ных чисел не яв­ля­ет­ся чле­ном по­сле­до­ва­тель­но­сти

     

    1)

    2)

    3)

    4)

    Ответ: 4
    9. B 4 № 137297. По­сле­до­ва­тель­ность за­да­на фор­му­лой . Сколь­ко чле­нов в этой по­сле­до­ва­тель­но­сти боль­ше 1?

     

    1) 8
    2) 9
    3) 10
    4) 11

    Ответ: 2
    10. B 4 № 137298. По­сле­до­ва­тель­но­сти за­да­ны не­сколь­ки­ми пер­вы­ми чле­на­ми. Одна из них — ариф­ме­ти­че­ская про­грес­сия. Ука­жи­те ее.

     

    1)

    2)

    3)

    4) ; ; ; ; ...

    Ответ: 3
    11. B 4 № 137299. Одна из дан­ных по­сле­до­ва­тель­но­стей яв­ля­ет­ся гео­мет­ри­че­ской про­грес­си­ей. Ука­жи­те эту по­сле­до­ва­тель­ность.

     

    1)

    2)

    3)

    4) ; ; ; ; ...

    Ответ: 2
    12. B 4 № 137300. Какая из сле­ду­ю­щих по­сле­до­ва­тель­но­стей яв­ля­ет­ся ариф­ме­ти­че­ской про­грес­си­ей?

     

    1) По­сле­до­ва­тель­ность на­ту­раль­ных сте­пе­ней числа 2.

    2) По­сле­до­ва­тель­ность на­ту­раль­ных чисел, крат­ных 5.

    3) По­сле­до­ва­тель­ность кубов на­ту­раль­ных чисел.

    4) По­сле­до­ва­тель­ность всех пра­виль­ных дро­бей, чис­ли­тель ко­то­рых на 1 мень­ше зна­ме­на­те­ля.

    Ответ: 2
    13. B 4 № 137301. Вы­пи­са­ны пер­вые не­сколь­ко чле­нов ариф­ме­ти­че­ской про­грес­сии: 3; 6; 9; 12;… Какое из сле­ду­ю­щих чисел есть среди чле­нов этой про­грес­сии?

     

    1) 83
    2) 95

    3) 100
    4) 102

    Ответ: 4
    14. B 4 № 137302. Ариф­ме­ти­че­ские про­грес­сии , и за­да­ны фор­му­ла­ми n-го члена:

    , ,

    Ука­жи­те те из них, у ко­то­рых раз­ность равна 4.

     

    1) и

    2) и

    3) , и

    4)

    Ответ: 2
    15. B 4 № 137303. В пер­вом ряду ки­но­за­ла 30 мест, а в каж­дом сле­ду­ю­щем на 2 места боль­ше, чем в преды­ду­щем. Сколь­ко мест в ряду с но­ме­ром n?

     

    1)

    2)

    3)

    4)

    Ответ: 1
    16. B 4 № 137304. Дана ариф­ме­ти­че­ская про­грес­сия: 33; 25; 17; … Най­ди­те пер­вый от­ри­ца­тель­ный член этой про­грес­сии.

     

    1)

    2)

    3)

    4)

    Ответ: 1
    17. B 4 № 137305. Ариф­ме­ти­че­ская про­грес­сия за­да­на усло­ви­я­ми: , . Какое из дан­ных чисел яв­ля­ет­ся чле­ном этой про­грес­сии?

     

    1) 80
    2) 56
    3) 48
    4) 32

    Ответ: 3
    18. B 4 № 137306. По­сле­до­ва­тель­ность за­да­на усло­ви­я­ми , . Най­ди­те .

    Ответ: -9
    19. B 4 № 137307. По­сле­до­ва­тель­ность за­да­на усло­ви­я­ми , . Най­ди­те .

    Ответ: 4
    20. B 4 № 137308. Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов ариф­ме­ти­че­ской про­грес­сии: …; 11; ; –13; –25; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой .

    Ответ: -1
    21. B 4 № 137309. В пер­вом ряду ки­но­за­ла 30 мест, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в преды­ду­щем. Сколь­ко мест в ряду с но­ме­ром ?

    Ответ: 28+2n
    22. B 4 № 137310. Дана ариф­ме­ти­че­ская про­грес­сия: 33; 25; 17; … . Най­ди­те пер­вый от­ри­ца­тель­ный член этой про­грес­сии.

    Ответ: -7
    23. B 4 № 311318. В гео­мет­ри­че­ской про­грес­сии из­вест­но, что . Найти пятый член этой про­грес­сии.

    Ответ: 32
    24. B 4 № 311330. Ариф­ме­ти­че­ская про­грес­сия за­да­на фор­му­лой n-го члена и из­вест­но, что . Най­ди­те пятый член этой про­грес­сии.

    Ответ: 1

    1

    25. B 4 № 311341. В ариф­ме­ти­че­ской про­грес­сии     из­вест­но, что  . Най­ди­те тре­тий член этой про­грес­сии.

    Ответ: -1
    26. B 4 № 311353. Гео­мет­ри­че­ская про­грес­сия     за­да­на фор­му­лой   - го члена   . Ука­жи­те чет­вер­тый член этой про­грес­сии.

    Ответ: -54
    27. B 4 № 311363. В ариф­ме­ти­че­ской про­грес­сии     из­вест­но, что   . Най­ди­те четвёртый член этой про­грес­сии.

    Ответ: 7
    28. B 4 № 311373. Гео­мет­ри­че­ская про­грес­сия     за­да­на фор­му­лой  n - го члена   . Ука­жи­те тре­тий член этой про­грес­сии.

    Ответ: 12
    29. B 4 № 311677. Дана ариф­ме­ти­че­ская про­грес­сия: Най­ди­те сумму пер­вых де­ся­ти её чле­нов.

    Ответ: 50
    30. B 4 № 311757. Дана ариф­ме­ти­че­ская про­грес­сия 14, 9, 4, ... Какое число стоит в этой по­сле­до­ва­тель­но­сти на 81-м месте?

    Ответ: -386
    31. B 4 № 311787. Дана ариф­ме­ти­че­ская про­грес­сия −19, −15, −11, ... Какое число стоит в этой по­сле­до­ва­тель­но­сти на 81-м месте?

    Ответ: 301
    32. B 4 № 311845. Дана ариф­ме­ти­че­ская про­грес­сия 11, 7, 3, ... Какое число стоит в этой по­сле­до­ва­тель­но­сти на 7-м месте?

    Ответ: -13
    33. B 4 № 311909. Ариф­ме­ти­че­ская про­грес­сия за­да­на усло­ви­я­ми: . Най­ди­те сумму пер­вых 19 её чле­нов.

    Ответ: 95
    34. B 4 № 311953. Дана гео­мет­ри­че­ская про­грес­сия (bn), зна­ме­на­тель ко­то­рой равен 2, а . Най­ди­те сумму пер­вых шести её чле­нов.

    Ответ: -47,25
    35. B 4 № 314399. Какое наи­боль­шее число по­сле­до­ва­тель­ных на­ту­раль­ных чисел, на­чи­ная с 1, можно сло­жить, чтобы по­лу­чив­ша­я­ся сумма была мень­ше 528?

    Ответ: 31
    36. B 4 № 314408. Най­ди­те сумму всех по­ло­жи­тель­ных чле­нов ариф­ме­ти­че­ской про­грес­сии 11,2; 10,8; …

    Ответ: 162,4
    37. B 4 № 314423. Какое наи­мень­шее число по­сле­до­ва­тель­ных на­ту­раль­ных чисел, на­чи­ная с 1, нужно сло­жить, чтобы по­лу­чив­ша­я­ся сумма была боль­ше 465?

    Ответ: 31
    38. B 4 № 314425. Най­ди­те сумму всех от­ри­ца­тель­ных чле­нов ариф­ме­ти­че­ской про­грес­сии –7,2; –6,9; …

    Ответ: -90
    39. B 4 № 314618. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 75, а сумма вто­ро­го и тре­тье­го чле­нов равна 150. Най­ди­те пер­вые три члена этой про­грес­сии.

     

    В от­ве­те пе­ре­чис­ли­те через точку с за­пя­той пер­вый, вто­рой и тре­тий члены про­грес­сии.

    Ответ: 25;50;100
    40. B 4 № 314619. Ариф­ме­ти­че­ская про­грес­сия (an) за­да­на усло­ви­я­ми: a1 = 3, an + 1 = an + 4. Най­ди­те a10.

    Ответ: 39

    41. B 4 № 314620. Гео­мет­ри­че­ская про­грес­сия ( ) за­да­на усло­ви­я­ми: . Най­ди­те

    Ответ: -2
    42. B 4 № 314628. За­пи­са­ны пер­вые три члена ариф­ме­ти­че­ской про­грес­сии: 20; 17; 14. Какое число стоит в этой ариф­ме­ти­че­ской про­грес­сии на 91-м месте?

    Ответ: -250
    43. B 4 № 314629. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 40, а сумма вто­ро­го и тре­тье­го чле­нов равна 120. Най­ди­те пер­вые три члена этой про­грес­сии.
    44. B 4 № 314632. За­пи­са­ны пер­вые три члена ариф­ме­ти­че­ской про­грес­сии: −6; 1; 8. Какое число стоит в этой ариф­ме­ти­че­ской про­грес­сии на 51-м месте?
    45. B 4 № 314633. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 48, а сумма вто­ро­го и тре­тье­го чле­нов равна 144. Най­ди­те пер­вые три члена этой про­грес­сии.

     

    В от­ве­те пе­ре­чис­ли­те через точку с за­пя­той пер­вый, вто­рой и тре­тий члены про­грес­сии.

    Ответ: 12;36;108
    46. B 4 № 314640. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 160, а сумма вто­ро­го и тре­тье­го чле­нов равна 40. Най­ди­те пер­вые три члена этой про­грес­сии.
    47. B 4 № 314650. В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 144, а сумма вто­ро­го и тре­тье­го чле­нов равна 72. Най­ди­те пер­вые три члена этой про­грес­сии.
    48. B 4 № 314653. Дана ариф­ме­ти­че­ская про­грес­сия (аn): −6, −2, 2, … . Най­ди­те a16.

    Ответ: 54
    49. B 4 № 316227. Дана ариф­ме­ти­че­ская про­грес­сия 8, 4 , 0, ... . Какое число стоит в этой по­сле­до­ва­тель­но­сти на 7-ом месте?

    Ответ: -16
    50. B 4 № 316254. Дана ариф­ме­ти­че­ская про­грес­сия: 11, 7, 3, ... . Какое число стоит в этой по­сле­до­ва­тель­но­сти на 7-м месте?

    Ответ: -13
    51. B 4 № 316280. Дана ариф­ме­ти­че­ская про­грес­сия: −15, −8, −1, ... . Какое число стоит в этой по­сле­до­ва­тель­но­сти на 6-м месте?

    Ответ: 20
    52. B 4 № 316317. Дана ариф­ме­ти­че­ская про­грес­сия: −18, −11, −4, ... . Какое число стоит в этой по­сле­до­ва­тель­но­сти на 21-м месте?

    Ответ: 122
    53. B 4 № 316343. Вы­пи­са­ны пер­вые не­сколь­ко чле­нов ариф­ме­ти­че­ской про­грес­сии: −87 ; −76; −65; … Най­ди­те пер­вый по­ло­жи­тель­ный член этой про­грес­сии.

    Ответ: 1
    54. B 4 № 316369. Вы­пи­са­ны пер­вые не­сколь­ко чле­нов ариф­ме­ти­че­ской про­грес­сии: 93; 85,5; 78; … Най­ди­те пер­вый от­ри­ца­тель­ный член этой про­грес­сии.

    Ответ: -4,5
    55. B 4 № 333009. Вы­пи­са­ны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской про­грес­сии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её чле­нов.

    Ответ: -1364

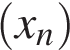    написать администратору сайта