Комплекс санның тригонометриялық түрі. Комплекс санның тригонометриялық турі. азастан Республикасы Білім жне ылым министрлігі Рымбек Байсейітов атындаы Семей аржыэкономикалы колледжі рмК
 Скачать 74.07 Kb. Скачать 74.07 Kb.
|
Қазақстан Республикасы Білім және ғылым министрлігі«Рымбек Байсейітов атындағы Семей қаржы-экономикалық колледжі» РМҚК«Математика» пәнінен ТҚЖ қолдану сабағы «Комплекс санның тригонометриялық турі» Оқытушы: Ыкласова А.Ж2017-2018 оқу жылы Комплекс сандар алгебралық теңдеулерді шешу негізінде пайда болды. Комплекс сан деп z=a+bi түріндегі санды айтамыз, мұндағы a және b –нақты сандар, ал i –жорамал бірлік, i2=–1. a комплекс санның нақты бөлігі, b –оның жорамал бөлігі. Re(z)= a,Im(z) =b 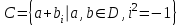 - комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі, - комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі, 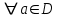 үшін үшін 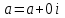 . .Комплекс сандар жиыны нақты сандар жиынының кеңеюі 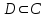 . .z=a+bi және 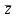 =a–bi өзара түйіндес сандар деп аталады =a–bi өзара түйіндес сандар деп аталады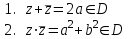 z1=a+bi және z2=c+di cандары тең 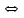 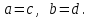 Комплекс сандарының қосындысы комплекс сан болады. 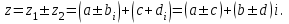 Қосудың қасиеттері: "z1,z2,z3C үшін (z1+z2)+z3=z1+(z2+z3), $0C, "zC , z+0=0+z=z , "zC, $ –zC, z+(–z)=(–z)+z=0 , "z1,z2C; z1+z2=z2+z1 . Комплек сандардың көбейтіндісі комплекс сан. z=z1×z2=(a+bi)×(c+di)=(ac–bd)+(bc+ad)i. Көбейтудің қасиеттері: "z1,z2,z3C (z1×z2)×z3=z1×(z2×z3) (ассоциативті), $1C, "zC, z×1=1×z=z (1=1+0×i), "zC, $ z-1C, z×z-1=z-1×z=1 (z=a+bi және z-1= 1/z=(a/(a2+b2))+((–b)/(a2+b2))i), "z1,z2C, z1×z2=z2×z1 (коммутативті). Қосу мен көбейту амалдары дистрибутивтілік заңымен байланысқан 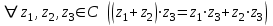 . .Комплекс сандардың бөліндісі комплекс сан, 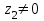 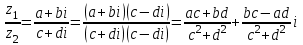 Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі. 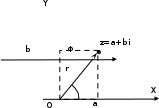 Комплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. Ox - осінің бойына комплекс санның нақты бөлігін (a=a+0∙i), ал Oy осінің бойына оның жорамал бөлігін орналастырсақ (bi=0+bi) жазықтықта әрбір комплекс сан z(a,b) нүктесі түрінде анықталады. 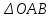 тік бұрышты тік бұрышты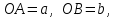 ïzï ïzï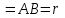 r=ïzï= r=ïzï=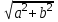 . . 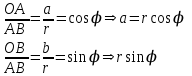 z=a+bi=r(cosφ+isinφ)- комплекс санның тригонометриялық түрі. 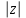 =r - комплекс санның модулі =r - комплекс санның модулі 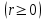 . .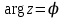 -комплекс санның аргументі. -комплекс санның аргументі.Тригонометриялық түрдегі комплекс сандарға амалдар қолдану өте жеңіл. Айталық, z1=r1(cosφ1+isinφ1), z2=r2(cosφ2+isinφ2) болсын. Онда 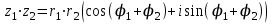 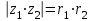 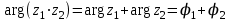 Егер 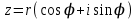 болса, онда болса, онда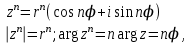 Муавр формуласы 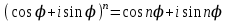 Комплекс саннан nші дәрежелі түбір табу және 1 ден табылған түбірлердің группасы. Айталық, а=r(cos 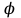 +isin +isin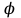 ) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін ) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін 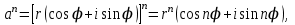 яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.  теңдігін пайдаланып , Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады. a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек 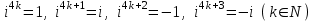 ескерсек жеткілікті.  Муавр формуласының дербес түрін қарастырайық. 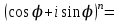 cos n cos n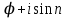 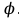 Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық. 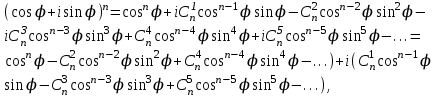 Мұндағы 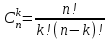 теңдігінің сол және оң жақ бөліктерін салыстырсақ, 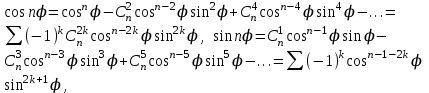 теңдіктерін аламыз. Сонымен, 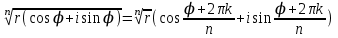 , мұндағы , мұндағы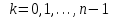 ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз. |
