Базы данных. Лекции - База данных, лекционный курс. Базы данных лекционный курс

• Название: Базы данных лекционный курс
• Анкор: Базы данных
• Дата: 10.03.2022
• Размер: 1.23 Mb.
• Имя файла: Лекции - База данных, лекционный курс.doc
• Тип: Документы; #390809
• страница: 5 из 11

Тогда

Право ÷ q

Пилот

Иванов

Сидоров

8) Соединение.

Естественноесоединение. Пусть r – отношение со схемой R, s – отношение со схемой S и R ∪ S = T. Естественным соединением отношений r и s (r ⊲⊳ s) является отношение q со схемой T, содержащее кортежи, каждый являющийся комбинацией кортежа из r и кортежа из s с равными (R ∩ S) – значениями.

Примечание. Если R ∩ S = ∅, то r ⊲⊳ s даст декартово произведение r и s.

Примеры:

а) Даны отношения k и m

k	(A	B)		m	(B	C)
	a1	b1			b1	c2
	а1	b2			b2	c1
	a2	b1

Тогда

k ⊲⊳m =	(A	B	C)
	a1	b1	c2
	a2	b1	c2
	a1	b2	c1

б) Даны отношения R1 и S1

R1 S1

№_П	ФИО_П	Город_П		№_Д	Название	Вес	Город_Д
Р1	Иванов И. И.	Москва		Д1	гайка	12	Москва
Р2	Сидоров С. С.	Киев		Д3	винт	17	Ростов
				Д6	шпилька	19	Москва

Естественное соединение R1 и S1 по атрибуту Город (в отношении R1 – это Город_П, а в отношении S1 – Город_Д):

R1 ⊲⊳ S1

№_П	ФИО_П	Город	№_Д	Название	Вес
Р1	Иванов И.И.	Москва	Д1	гайка	12
Р1	Иванов И.И.	Москва	Д6	шпилька	19

Тета – соединение. При естественном соединении отношения могут комбинироваться только по одноименным столбцам и должны комбинироваться по всем таким столбцам.

Примечание. В предыдущем примере вначале была применена операция переименования атрибутов Город_Д и Город_П на Город.

Отношения могут соединяться также по столбцам с различными именами атрибутов, но равными доменами.

Тета – соединение отношений r и s по столбцам i и j 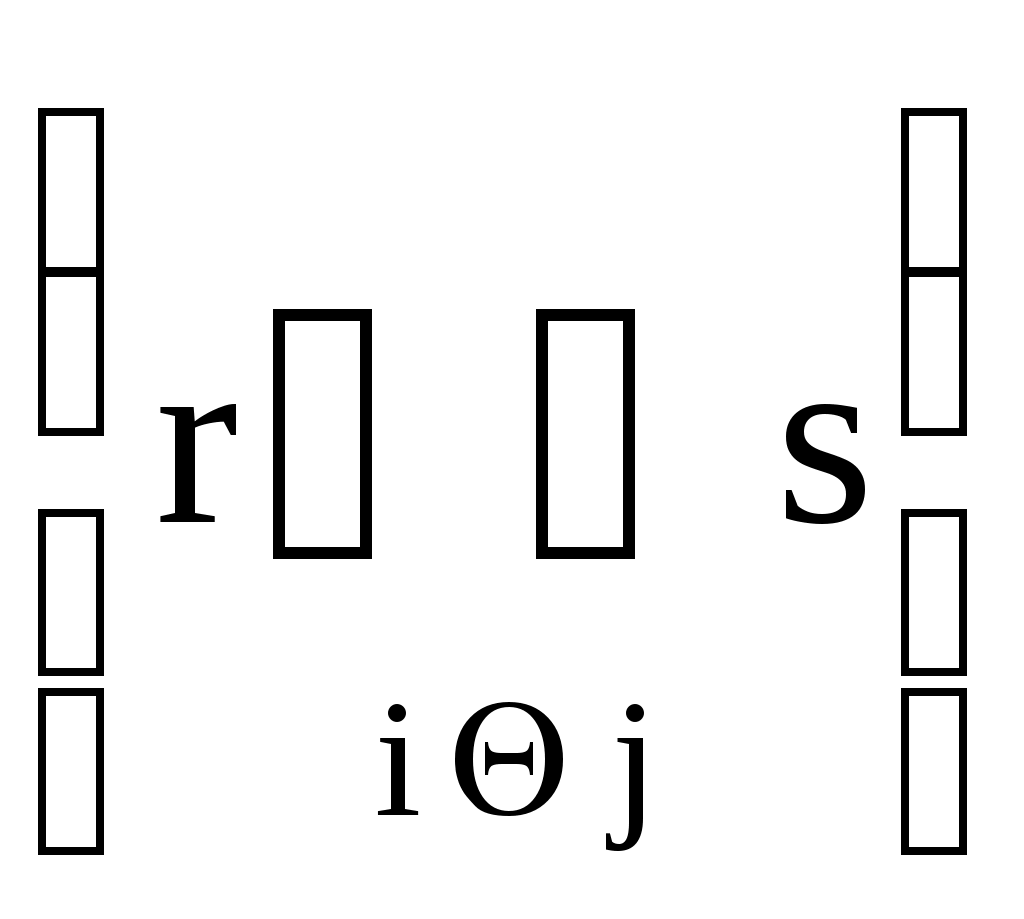представляет собой множество кортежей в декартовом произведении r и s, таких, что i-й элемент r находится в связи Θ с j–элементом s.

Если Θ является оператором «=», то эта операция называется эквисоединением.

Примеры

а) Пусть R1 – отношение, содержащее информацию о рейсах из города «а» в город «в», S1 – отношение, содержащее информацию о рейсах из города «в» в город «с»:

R1

Номер	Время_вылета	Время_прибытия
60	9.40	11.45
91	12.50	14.47
112	16.05	18.15
306	20.30	22.25
420	21.15	23.11

S1

Номер	Время_вылета	Время_прибытия
11	8.30	9.52
60	12.25	13.43
156	16.20	17.40
158	19.10	20.35

Требуется узнать, какие рейсы из «a» в «в» сочетаются с рейсами из «в» в «c».

Для этого необходимо соединить те кортежи, для которых Время_прибытия в отношении R1 меньше Время_вылета в отношении S1.
Тета – соединение отношений R1 и S1:

Номер	Время_вылета	Время_прибытия	Но­мер	Время_вылета	Время_прибытия
60	9.40	11.45	60	12.25	13.43
60	9.40	11.45	156	16.20	17.40
60	9.40	11.45	158	19.10	20.35
91	12.50	14.47	156	16.20	17.40
91	12.50	14.47	158	19.10	20.35
112	16.05	18.15	158	19.10	20.35

б) Даны отношения Маршрут и Адрес

Маршрут

Номер	Пункт_отправления	Пункт_назначения
84	Чикаго	Нью-Йорк
109	Нью-Йорк	Лос-Анджелес
117	Атланта	Бостон
213	Нью-Йорк	Бостон
214	Бостон	Нью-Йорк