МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ УББ НА ПАСИВНОМ УЧАСТКЕ ТРАЕКТОРИИ. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ МБР НА АКТИВНОМ УЧАСТКЕ ТРАЕКТОРИ. Ббк 34. 4 Авторы Саратовцев Д. А., 242 уч группа
 Скачать 186.41 Kb. Скачать 186.41 Kb.
|
|
ББК 34.4 Авторы: Саратовцев Д.А., 242 уч. группа Тюрин В.Ю., 242 уч. группа Ермаков Д.С. 243уч. группа. Научный руководитель: канд. тех. наук подполковник Щедрин Е.А. Военной академии РВСН им. Петра Великого (филиал г. Серпухов) МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ МЕКОНТИНЕНТАЛЬНОЙ БАЛЛИСТИЧЕСКОЙ РАКЕТЫ НА АКТИВНОМ УЧАСТКЕ ТРАЕКТОРИИ Точность попадания ББ в точку цели характеризуется ошибками управления. Ошибки разделяются на инструментальные, обусловленные несовершенством приборов и систем, и методические, обусловленные несовершенством методов измерений. Считая, что инструментальные ошибки близки к идеальным значениям, то для понижения методических ошибок необходимо применять новые (перспективные) методы и алгоритмы управления. В теории автоматического управления можно повысить точностные характеристики за счет усовершенствования методик синтеза алгоритма управления. Необходимость повышения точности МБР, обусловлена повышением эффективность их боевого применения, снижения кругового вероятностного отклонения, повышая живучесть ракеты снижения массы ракеты. Таким образом данная тема исследования актуальна. Цель статьи: исходя вышеизложенного целью является, получения системы дифференциальных уравнений движения МБР для ее дальнейшего использования при синтезе алгоритма управления. Для управления ОУ нужно знать его модель. В качестве модели ракеты можно рассматривать закон его движения на различных участках траектории. На атмосферном участке полета МБР на ракету действуют следующие силы: сила тяги двигательной установки 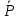 , управляющая сила , управляющая сила 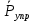 , аэродинамическая сила , аэродинамическая сила 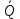 , сила притяжения Земли , сила притяжения Земли 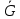 . На внеатмосферном участке траектории на МБР действуют силы: сила тяги двигательной установки . На внеатмосферном участке траектории на МБР действуют силы: сила тяги двигательной установки 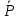 , управляющая сила , управляющая сила 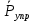 , сила притяжения Земли , сила притяжения Земли 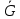 . .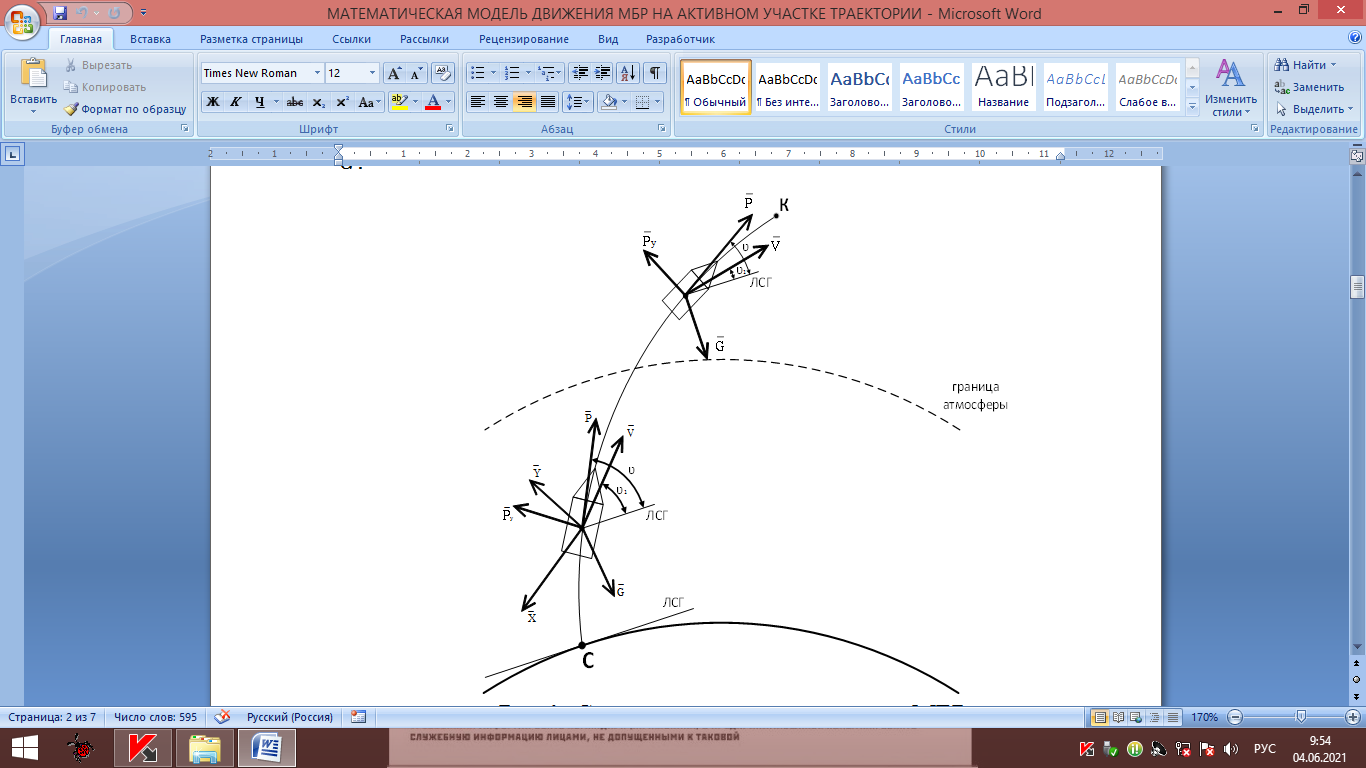 Рисунок 1. Схема траектории движения МБР Сила тяги 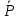 ракетного двигателя создается за счет сгорания топлива и выброса с большой скоростью продуктов сгорания через сопло и пределах атмосферы на высоте h определяется соотношением: ракетного двигателя создается за счет сгорания топлива и выброса с большой скоростью продуктов сгорания через сопло и пределах атмосферы на высоте h определяется соотношением: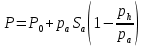 , (1) , (1)где 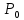 – сила тяги на поверхности земли – сила тяги на поверхности земли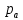 – давление газов на срезе сопла – давление газов на срезе сопла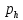 –статическое давление окружающего воздуха –статическое давление окружающего воздуха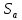 – площадь среза сопла. – площадь среза сопла.Сила тяги 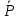 ракетного двигателя вне атмосферы равна: ракетного двигателя вне атмосферы равна: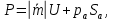 (2) (2)где 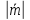 – массовый секундный расход топлива – массовый секундный расход топлива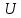 – скорость истечения. – скорость истечения.Управляющая сила 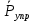 создается за счет поворота и отклонения органов управления ракеты, которые стремятся направить ракету по попадающей траектории и определяется выражением: создается за счет поворота и отклонения органов управления ракеты, которые стремятся направить ракету по попадающей траектории и определяется выражением: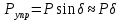 , (3) , (3)где 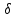 – угол отклонения органов управления. – угол отклонения органов управления.Аэродинамическая сила 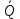 возникает от набегающего потока воздуха и равна: возникает от набегающего потока воздуха и равна: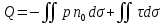 , (4) , (4)где 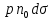 – сила нормального давления – сила нормального давления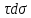 – касательная сила. – касательная сила.Сила притяжения Земли 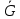 – гравитационная сила, которая возникает в результате взаимодействия гравитационных полей Земли и ракеты, и определяется выражением: – гравитационная сила, которая возникает в результате взаимодействия гравитационных полей Земли и ракеты, и определяется выражением: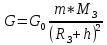 , (5) , (5)где 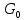 – универсальная постоянная тяготения – универсальная постоянная тяготения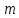 – масса ракеты – масса ракеты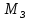 – масса Земли – масса Земли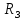 – средний радиус Земли – средний радиус Земли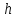 – расстояние между центом массы ракеты и поверхностью Земли. – расстояние между центом массы ракеты и поверхностью Земли.На основании второго закона Ньютона 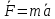 (6) (6)составим систему уравнений движения ракеты в пределах атмосферы с проекцией на оси гироскопической системы координат:  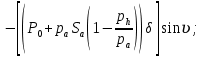 (7) (7)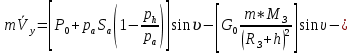 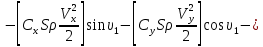 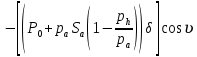 , (8) , (8)где, 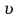 – угол тангажа – угол тангажа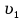 – угол наклона вектора скорости к плоскости стартового горизонта. – угол наклона вектора скорости к плоскости стартового горизонта.Отсюда полное ускорение ракеты равно: 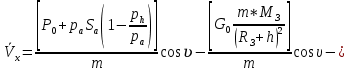 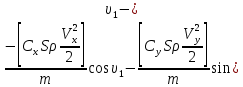 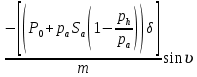 ; (9) ; (9)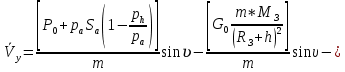 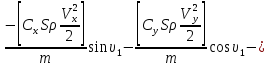 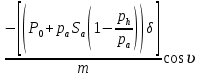 . (10) . (10)Т.к. ускорение это производная от скорости 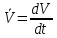 , то полная скорость в операторной форме будет ровна: , то полная скорость в операторной форме будет ровна: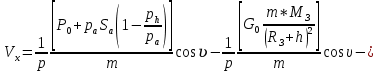 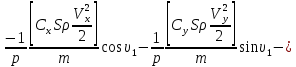 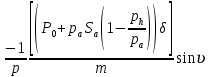 ; (11) ; (11)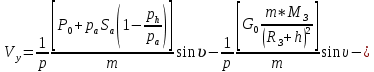 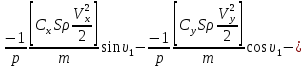 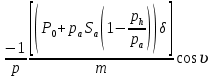 . (12) . (12)Т.к. скорость это производная от пути 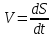 , то положение ракеты в операторной форме будет ровна: , то положение ракеты в операторной форме будет ровна: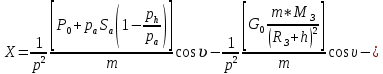 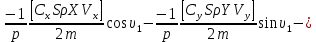 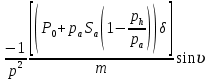 ; (13) ; (13)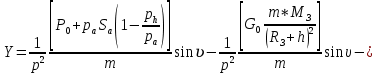 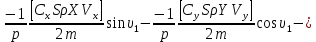 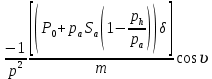 . (14) . (14)В малоугловом приближение 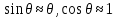 получим получим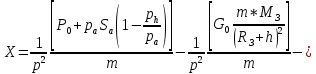 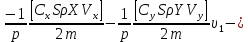 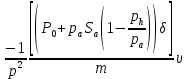 ; (15) ; (15)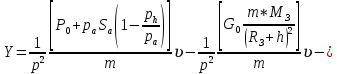 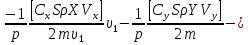 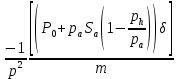 . (16) . (16)Для упрощения записи, введем следующие обозначения: 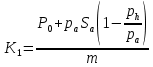 ; (17) ; (17)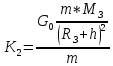 ; (18) ; (18)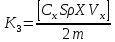 ; (19) ; (19)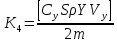 ; (20) ; (20)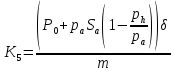 ; (21) ; (21)Таким образом, система уравнений принимает следующий вид: 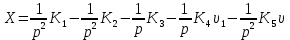 ; (22) ; (22)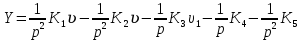 .(23) .(23)Так как после выхода МБР перестает действовать полная аэродинамическая сила, то система уравнений принимает следующий вид: 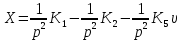 ; (24) ; (24)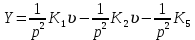 . (25) . (25)Вывод: на основе вышеописанной системы уравнений можем построить замкнутую систему автоматического управления (САУ), которая будет реализовывать принцип повышения эффективности применения за счет увеличения точности наведения ракет. Литература: Нижегородов А.А., Пискулин Е.В., Щедрин Е.А. /Системы управления летательными аппаратами /Учебник МО РФ – Серпухов 2017. Пушкарев Ю.А., Пушкарева Е.Ю. /Теория автоматического управления/ Учебник МО РФ – Серпухов 2010. Югрина Е.И. Правила оформления выпускной квалификационной работы. Методическое пособие. Серпухов 2012. |
