ЖБК 200 вопросов и ответов. Бетон, арматура и железобетон

• Название: Бетон, арматура и железобетон
• Анкор: ЖБК 200 вопросов и ответов.doc
• Дата: 07.02.2017
• Размер: 11.86 Mb.
• Имя файла: ЖБК 200 вопросов и ответов.doc
• Тип: Документы; #2374
• страница: 42 из 53

152. В ЧЕМ СУТЬ РАСЧЕТА ПО ОБРАЗОВАНИЮ НОРМАЛЬНЫХ ТРЕЩИН ПРИ ИЗГИБЕ?

Суть  в выполнении условия М  М_crc, где М  изгибающий момент в нормальном сечении от внешней расчетной нагрузки, а М_crc  момент внутренних сил, который сопротивляется образованию трещин.

Чтобы вызвать образование трещин в сечении преднапряженного изгибаемого элемента, нужно загрузить его внешним моментом, численно равным М_crc и состоящим из двух слагаемых: М_р  момента, который погашает предварительное обжатие крайнего волокна бетона (на рис. 75  нижнего), т.е. уменьшает в нем сжимающие напряжения от _bp до 0, и М_bt  момента, который повышает в этом же волокне растягивающие напряжения от 0 до сопротивления бетона растяжению R_bt,ser. Очевидно, что при отсутствии преднапряжения первое слагаемое отсутствует.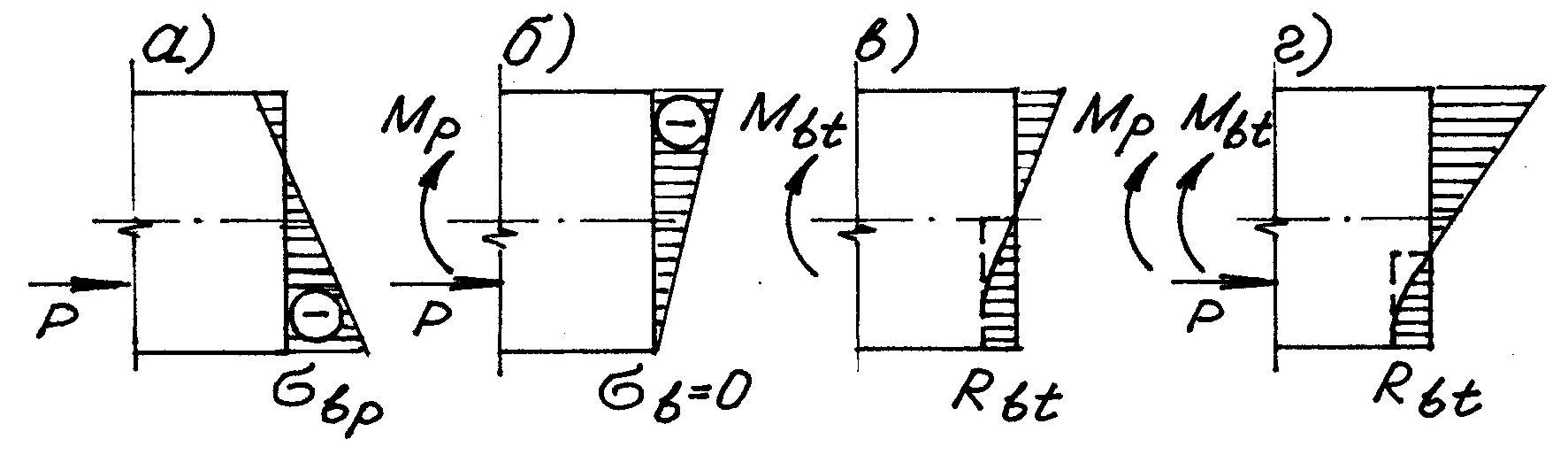



Рис. 75
Поскольку М_р = W_red_bp, а _bp = P/A_red + Pe_op / W_red (см. вопрос 49), то подставив второе выражение в первое, получим (рис. 76,а):

M_p = W_red (P/A_red + Pe_op /W_red) = P(r + e_op),

где r = W_red /A_red  расстояние от центра тяжести приведенного сечения до верхней ядровой точки (радиус ядра сечения). Для учета неупругих свойств бетона вводят поправочный коэффициент , составляющий в зависимости от напряжений в сжатом бетоне от0,7 до 1. Тогда r = =W_red /A_red. Другими словами, М_р  это момент силы обжатия Р относительно ядровой точки, наиболее удаленной от растянутого волокна, обозначается он М_rp.

M_bt = W_pl R_bt,ser  обычная формула сопромата, в которую только внесена поправка на неупругие деформации бетона растянутой зоны: W_pl  упруго-пластический момент сопротивления приведенного сечения. Его можно определить по формулам Норм или из выражения W_pl = W_red, где W_red  упругий момент сопротивления приведенного сечения для крайнего растянутого волокна (в нашем случае  нижнего),  = (1,25...2,0)  зависит от формы сечения и определяется по таблицам справочников. R_bt,ser  расчетное сопротивление бетона растяжению для предельных состояний 2-й группы (численно равное нормативному R_{bt, n}).



Рис. 76

153. ПОЧЕМУ НЕУПРУГИЕ СВОЙСТВА БЕТОНА УВЕЛИЧИВАЮТ МОМЕНТ СОПРОТИВЛЕНИЯ СЕЧЕНИЯ?

Рассмотрим простейшее прямоугольное бетонное (без арматуры) сечение и обратимся к рис.75,в, на котором показана расчетная эпюра напряжений накануне образования трещин: прямоугольная в растянутой и треугольная в сжатой зоне сечения. По условию статики равнодействующие усилий в сжатой N_b и в растянутойN_bt зонах равны между собой, значит равны и соответствующие площади эпюр, а это возможно, если напряжения в крайнем сжатом волокне вдвое больше растягивающих: _b= 2R_bt,ser. Равнодействующие усилий в сжатой и растянутой зонах N_b = =N_bt = R_bt,serbh /2, плечо между ними z = h /4 + h /3 = 7h /12. Тогда момент, воспринимаемый сечением, равен M = N_btz =(R_bt,serbh/2)(7h/12)= =R_bt,serbh²7/24 = R_bt,ser(7/4)bh²/6, или M = R_bt,ser1,75 W. То есть, для прямоугольного сечения = 1,75. Таким образом, момент сопротивления сечения возрастает благодаря принятой в расчете прямоугольной эпюре напряжений в растянутой зоне, вызванной неупругими деформациями бетона.