математика 6 класс. Математика 6кл - Конспект.. Фигуры на плоскости, симметричные относительно точки
 Скачать 195.02 Kb. Скачать 195.02 Kb.
|
|
Субботина Ирина Юрьевна учитель математики МБОУ «Кайрактынская СОШ» Математика 6 класс Математика 6 класс С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин М., Просвещение, 2014 г. Уровень обучения базовый. Тема урока: Фигуры на плоскости, симметричные относительно точки. Количество часов на изучение темы: 1 час Урок изучения нового материала. Цель урока: Ознакомить учащихся с понятием симметрии относительно точки. Сформировать навыки строить фигуры на плоскости, симметричные относительно точки. Задачи: Образовательные: познакомить учащихся с новым понятием, сформировать умения и навыки построения фигуры, симметричной данной относительно точки; Развивающие: развитие ЗУН по теме данного урока, развитие мыслительной деятельности, развитие творческой деятельности; Воспитательные: формирование эстетических навыков при оформлении записей, выполнении чертежей, формирование трудолюбия и самостоятельности. Планируемые результаты: Предметные: Знают понятие симметрии относительно точки. Умеют строить фигуры на плоскости, симметричные относительно точки. Метапредметные: Регулятивные: различают способ и результат действий. Познавательные: владеют общим приёмом решения задач. Коммуникативные: договариваются о совместной деятельности, приходят к общему решению, в том числе в ситуации столкновения интересов. Личностные: Имеют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений Техническое обеспечение урока: компьютер, проектор, экран. Дополнительное методическое и дидактическое обеспечение урока: Рабочая тетрадь по математике к учебнику «Математика. 6 класс» М.К. Потапов, А.В. Шевкин, М: «Просвещение», 2014, «Математика. Методические рекомендации. 6 класс» М.К. Потапов, А.В. Шевкин. М., Просвещение , 2013 г. Содержание урока: 1. Организационный момент. 2. Актуализация знаний обучающихся. Демонстрация слайдов с изображениями проявлений симметрии в природе, в продуктах человеческой деятельности; Учитель предлагает учащимся назвать симметричные фигуры в окружающем мире. 3. Изучение нового материала. Построим координатную ось. Изобразим числа 3 и –3 (рис.1). Видим, что точки А(3) и удалены от начала отсчёта на одинаковое расстояние. При этом говорят, что они симметричны относительно точки О. Определение. Точки А и В называют симметричными относительно точки О, если эти три точки лежат на одной прямой и точка О делит отрезок на две равные части. 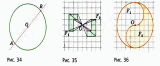 На рисунке 34 (учебник)окружность с центром в точке О пересекает прямую в точках А и В. А, О, В – лежат на одной прямой и АО = ОВ. Т.о. точки А и В – симметричны относительно точки О. Если точку А повернуть на 1800 вокруг точки О (по окружности), то она совместится с точкой В. Н 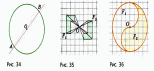 а рис. 35 показаны фигуры F1 и F2 и точка О. Если одну из этих фигур повернуть на 1800, то она совместится с другой фигурой (т.е. фигуры совпадут при наложении их друг на друга). а рис. 35 показаны фигуры F1 и F2 и точка О. Если одну из этих фигур повернуть на 1800, то она совместится с другой фигурой (т.е. фигуры совпадут при наложении их друг на друга).F1 и F2 – симметричны относительно точки О. Фигуры F1 и F2 равны, пишут: F1 = F2. Н 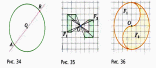 а рис. 36 показаны фигуры F1 и F2 и точка О. Если одну из этих фигур повернуть на 1800, то она совместится с другой фигурой (т.е. фигуры совпадут при наложении их друг на друга). а рис. 36 показаны фигуры F1 и F2 и точка О. Если одну из этих фигур повернуть на 1800, то она совместится с другой фигурой (т.е. фигуры совпадут при наложении их друг на друга).F1 и F2 – симметричны относительно точки О. Фигуры F1 и F2 равны, пишут: F1 = F2. Пример 1.Даны точки А и О. Постройте точку А1, симметричную точке А относительно точки О. Решение. Требуется построить точку А1 так, чтобы она была симметрична точке А относительно точки О. При этом центр симметрии О будет серединой отрезка АА1. Проведем из точки А через центр симметрии О луч АО. На луче АО, с помощью циркуля, отложим отрезок ОА1 так, чтобы ОА1 = ОА.  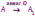 т.к. точки А, О, А1 лежат на одной прямой и ОА = ОА1). Пример 2. Дан отрезок АВ и точка О, не принадлежащая ему. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О. Решение. Требуется построить отрезок А1В1 так, чтобы он была симметричен отрезку АВ относительно точки О. При этом центр симметрии О будет серединой каждого из отрезков АА1 и ВВ1. Проведем из точки А через центр симметрии О луч АО. На луче АО, с помощью циркуля, отложим отрезок ОА1 так, чтобы, ОА1 = ОА. Проведем из точки В через центр симметрии О луч ВО. На луче ВО, с помощью циркуля, отложим отрезок ОВ1 так, чтобы, ОВ1 = ОВ.  1) 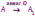 (т.к. точки А, А1, О лежат на (т.к. точки А, А1, О лежат наодной прямой и ОА = ОА1). 2) 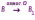 (т.к. точки В, В1, О лежат на (т.к. точки В, В1, О лежат наодной прямой и ОВ = ОВ1). 3) Значит 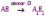 . .Пример 3. Дан треугольник АВС и точка О вне этого треугольника. Постройте треугольник А1В1С1, симметричный треугольнику АВС относительно точки О. Решение. Требуется построить треугольник А1В1С1 так, чтобы он была симметричен треугольнику АВС относительно точки О. При этом центр симметрии О будет серединой каждого из отрезков АА1, ВВ1и СС1. Проведем из точки А через центр симметрии О луч АО. На луче АО, с помощью циркуля, отложим отрезок ОА1 так, чтобы, ОА1 = ОА. Проведем из точки В через центр симметрии О луч ВО. На луче ВО, с помощью циркуля, отложим отрезок ОВ1 так, чтобы, ОВ1 = ОВ. Проведем из точки С через центр симметрии О луч СО. На луче СО, с помощью циркуля, отложим отрезок ОС1 так, чтобы, ОС1 = ОС. 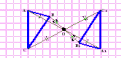 1) 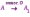 (т.к. точки А, А1, О лежат на одной прямой и ОА = ОА1). (т.к. точки А, А1, О лежат на одной прямой и ОА = ОА1).2) 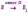 (т.к. точки В, В1, О лежат на одной прямой и ОВ = ОВ1). (т.к. точки В, В1, О лежат на одной прямой и ОВ = ОВ1).3) 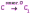 т.к. точки С, С1, О лежат на одной прямой и ОС = ОС1. т.к. точки С, С1, О лежат на одной прямой и ОС = ОС1.4) Значит . 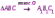 4. Тренировочные упражнения. Уч.с.80 № 396. Какая точка координатной оси симметрична относительно начала координат точке: а) 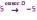 ; б) ; б) 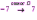 ; в) ; в) 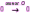 . .Уч.с.80 № 398(а-в). По рисунку 50 определите, какая точка симметрична относительно точки О точке: а 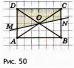 ) ) 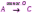 ; ;б) 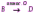 ; ;в)  . .Уч.с.80 № 399(а-г). По рисунку 50 определите, какой отрезок симметричен относительно точки О отрезку: а 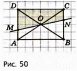 ) ) 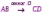 ; б) ; б) 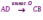 ; ;в) 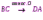 ; г) ; г) 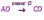 . .Уч.с.80 № 400(а,г,д). По рисунку 50 определите, какой фигуре симметричен относительно т 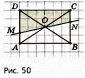 очки О: очки О:а) 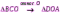 ; ;г) 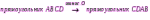 ; ;д) 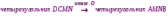 . .5. Итоги урока. Что нового вы узнали на уроке? Что вам понравилось? Не понравилось? Что показалось вам трудным в этой теме? Домашнее задание: .§ Д.1 (выучить теорию). № 398(г-ж), 399(д-з), 400(б,в) + доп.задания. № 401. |
