оибр. Документ Microsoft Word. Безусловная проекция
 Скачать 18.44 Kb.
|
|
Безусловная проекция T[Z] отклонения T[A] на некоторое подмножество атрибутов Z€A получается удалением из T[A] всех столбцов имена которых не принадлежат множеству Z (принадлежат множеству A\Z)с постоянным удалением лишних экземпляров один.строк ,если они возникли в рез-те удаления столбцов .Применяется с целью сокращения путем удаления столбцов ,соответствующих несущественных параметров. Z=[Y1;Y3]Следует T[Z] ={1.1, 2.1}
2)T[1,{Y1,Y2}]=(1,1)(1,2)(1,3) 3)T{q1,1,{Y1,Y2}}={1,1} Применение :Анализ большого обьема ИД с целью выявления н\р несущественных параметров , обычно очень трудоемкий процесс. НО его можно разделить на легкие процессы . Система открытая по входу нарушен баланс между входом и выходом .Восстановление этого баланса осуществляется огрублением значений вых переменных путем перехода и классом значений которые являются классами эквивалентности заданных на множестве Y.для систем открытых по входу выполняется отображение 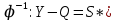 которое каждому картежу значений вых переменных сопоставляет ед.состояние при этом некторые кортежи соответсвуют одному и тому же состоянию.Китайский почтальон 1)для исходной не эйлеровой модели построить Q+ и Q- множества 2)Найти веса всех кратчайших путей Δt от a к b (1 этап алг.Дейкстры) 3)Для найденных весов решить транспортную задачу и тем самым определить БМИП c минимальным суммарным весом которую необх ввести в модель для получения эйлеровой модели 4)Построить сами кратчайшие пути (2 этап алг. ДЕйкстры) 5)Добавляем дуги построенных кратчайших путей чтобы каждая была в 4 экземплярах в иттоге получаем эйлерову модель 6)построить эйлеров обход для модели , исп. Алг. Флери 1этап) Алг дейкстры 1)удалить из МОИ все петлевые дуги а также параллельные оставляя дуги с наим весом ,положить все состояния + равным 0 и считать a0 – сост. С постоянным весом 2)Для всякого а не равного а0 положить V(a)=бесконечность и как начальный временный вес 3)из всех состояний с временным весом выделить те для которых V(ai)-V(p)> Δt 4)выбрать сост с мин нач весом присвоить переменной p значение aj и считать а с пост-м весом 5)если среди сост с пост весом находятся все состояния из множества Q то закончить 1 этап и считать весами кратчайших путей из а0 2 этап алг дейкстры Построитть кратчайшие пути из а в б |