Билеты по геометрии 7 класс
Билет №1.
Точка-это простейшая геометрическая фигура. Точки обозначают Заглавными латинскими буквами , прямая- это геометрическая фигура, не имеющая ни начала ни конца. Через две точки можно провести прямую, Притом только одну. Прямую обозначают маленкой латинской буквой . ,отрезок-это прямая ограниченная двумя точками. Обозначается двумя Заглавными латинскими буквами.
Первый признак равенства треугольников (с доказательством).
ТЕОРЕМА: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство: Расмотрим тереугольники АВС и А1В1С1 у которых АВ=А1В1, АС=А1С1 , углы А и А1. Докажем, что АВС=А1В1С1
Найдите величины смежных углов, если один из них в 5 раз больше другого. 1 угол х, второй тогда будет 5х, а сумма смежных углов составляет 180* x+5x=180 6x=180 x=30 первый угол -30, второй 5 раз больше, значит 5*30=150 Ответ:30 и 150
Билет №2.
Луч- это прямая, которая имеет начало и не имеющая конца.
дополнительные лучи- лучи, на которые точка разбивает прямую.
плоскость и полуплоскость:
Плоскость- поверхность, которая содержит прямую и любые
её две точки.
Полуплоскость- геометрическая фигура состоящия из множесьва точек плоскости,
лежащих по одну сторону от прямой на этой плоскости.
Второй признак равенства треугольников (с доказательством).
ТЕОРЕМА:Если сторона и два прилежащих к ней угла одного треугольника
соответствено равны стороне и двум прилежащим к ней углам другово треугольника, то
такие треугольники равны.
Доказательство: Расмотрим тереугольники АВС и А1В1С1 у которых АВ=А1В1
,А=А1, углы В=В1. Докажем, что АВС=А1В1С1
Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А
совместиласть с с вершиной А1 , сторона АВ - с равной её стороной А1В1, и вершины С
и С1 оказались по одну сторону от прямой А1В1
Так как А=А1 и В=В1 , то сторона АС наложится на лучь А1С1 а сторона ВС- на лучь
В1С1. Поэтому вершина С- общая тоска сторон АС и ВС- окажется лежащей на луче
А1С1, так и на луче В1С1 и, следовательно, совместится с общей точкой этих лучей-
вершиной С1. Значит, совместятся стороны АС и А1С1, ВС и В1С1.
Итак, треугольники АВС и А1В1С1 полностью совместятся, по этому они равны.
равны. Теорема доказана.
Отрезки MN и DK пересекаются в их общей середине B. Докажите равенство треугольников MDB и NKB. Расмотрим треугольники MDB и NKB:
1)MB=BN по условию 2)DB=BK по условию 3)угол MDB= углу NBK т.к. вертикальные
Треугольник MDB равен треугольнику NKB по двум сторонам и углу между ними.
Теорема доказана
Билет №3.
Угол- геометрическая фигура, которая состоит из точки и лучей исходяших из этой точки. Виды углов- прямой угол, острый угол, тупой угол, развёрнутый угол. Биссектриса угла- это лучь исходящий из вершины угла и делящий его на два равных угла.
Третий признак равенства треугольников (с доказательством).
Теорема:Если три стороны одного треугольника равны соответствено трём сторонам
другого треугольника, то такие треугольники равны.
Доказательство:Расмотрим треугольники ABC и A1B1C1 у которых AB=A1B1, BC=B1C1,
CA=C1A1. Докажем что ABC=A1B1C1
Расположим треугольники ABC и A1B1C1 так, чтобы вершина A соовместилась с
вершиной A1, вершина B - с B1 , а вершины C и C1 лежали на разных полу плоскостях
относительно прямой AB. Проведём отрезок CC1. Так как AC=A1C1, то треугольник C
Найдите периметр равнобедренного треугольника ADC с основанием AD, если AD = 7 см, DC = 8 см.
Дано:АDC- равнобедреный
Найти: Периметр ADС
Решение: DC=AC (т.к. ADC- равнобедреный) Периметр ADC=AD+DC+AC. Периметр
7+8+8=23 Ответ:P ADC=23см
|
Билет №4.
Треугольник- это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков попарно соединяющих эти точки. Точки называбт верщинами, а отрезки- его сторонами.
Виды треугольников: треугольник у которого все стороны равны называют равностороним.
Равнобедреный треугольник это треугольник у которого две стороны равны, равные стороны
называются боковыми а нижняя основанием.
Разностороний треугольник это треугольник у которого нет ни одной равной стороны
Прямоугольный треугольник это треугольник у которого одна сторона равна 90 он называется
пряугольный угол, сторона лежащая против прямого угол гипотенузой две другие катетами.
Теорема о биссектрисе равнобедренного треугольника, проведенной к основанию (с доказательством).
Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126° .
Билет №5.
Треугольник. Элементы треугольника.
Теорема об угле в 300 в прямоугольном треугольнике (с доказательством).
Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR.
Билет №6.
Измерение отрезков и углов.
Теорема о двух прямых перпендикулярных к третьей прямой (с доказательством).
Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.
|
Билет №7.
Смежные и вертикальные углы.
Свойство углов равнобедренного треугольника (с доказательством).
Найдите углы треугольника, на которые высота разбивает равносторонний треугольник
Билет №8.
Теорема. Обратная теорема. Следствие. Доказательство методом от противного.
Признак равенства прямоугольных треугольников по гипотенузе и катету (с доказательством).
Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .
Билет №9.
Перпендикулярные прямые. Перпендикуляр к прямой.
Первоесвойство равнобедренного треугольника (с доказательством).
Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126° .
Билет №10.
Равнобедренный треугольник.
Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)
Найдите смежные углы, если один из них на 55° больше другого.
Билет №11.
Равносторонний треугольник и его свойства.
Обратная теорема об угле в 300 в прямоугольном треугольнике (с доказательством).
Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO.

|
Билет №12.
Прямоугольный треугольник.
Определение медианы треугольника. Свойство медианы равнобедренного треугольника (с доказательством).
3.Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что AC= 17 см, угол ABC равен 84° .
|
Билет № 13.
Признаки равенства прямоугольных треугольников. (Доказательство одной из теорем по выбору учащегося.)
Свойство вертикальных углов.
Докажите равенство отрезков, соединяющих середину основания равнобедренного треугольника с серединами боковых сторон.
Билет №14.
Третий признак равенства треугольников (с доказательством).
Отрезок. Построение середины отрезка.
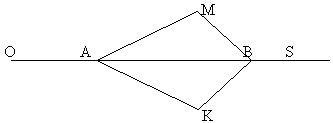
Известно, что 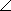 OAM = OAM = 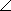 OAK и OAK и 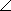 MBS = MBS = 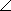 KBS. Докажите, что AK = AM,BM = BK. KBS. Докажите, что AK = AM,BM = BK.
|
Билет №15.
Определение угла. Построение угла, равного данному.
Теорема о сумме углов треугольника (с доказательством).
Прямая а пересекает стороны угла A. Докажите ,что 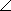 1 = 1 = 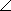 2, если известно, что 2, если известно, что 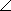 5 = 5 = 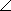 6. 6.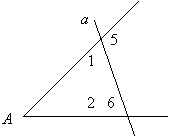
Билет №16.
Определение треугольника. Построение треугольника по трем сторонам.
Теорема о внешнем угле треугольника (с доказательством).
Найдите углы при основании MP равнобедренного треугольника МОР,если MK – его биссектриса и 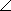 OKM = 96°. OKM = 96°.
Билет №17.
Равные треугольники. Неравенство треугольника. Соотношения между сторонами и углами треугольника.
Определение внешнего угла. Свойство внешнего угла.
В треугольнике MOK 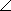 O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника. O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.
Билет №18.
Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)
Теорема о сумме углов прямоугольного треугольника (с доказательством).
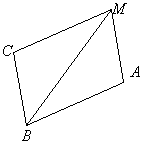
Отрезки AB и CM параллельны и равны. Докажите, что AM = BC.
|
Билет №19.
Окружность. Хорды, дуги, радиус, диаметр.
Определение параллельных прямых. Признаки параллельности прямых (доказательство одного из признаков по выбору учащегося).
Докажите, что AB = CM.
|
Билет №20.
Определение биссектрисы угла. Построение биссектрисы угла.
Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)
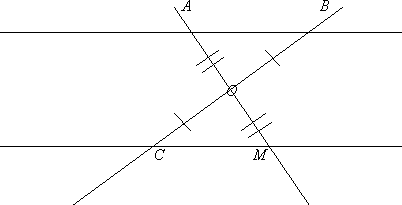
Треугольник MCB – равносторонний, BK и MP – его медианы, пересекающиеся в точке O.
Докажите равенство треугольников BOP и MOK.
| |
 Скачать 29.63 Kb.
Скачать 29.63 Kb.