10-тригонометриялық теңдеулер және олардың жүйелерін шешу. Білімдерін тексеру Кім жылдам ойыны бойынша ткен материалдарды срап шыу
 Скачать 106.08 Kb. Скачать 106.08 Kb.
|
23-дәріс. 4.6. Тригонометриялық теңдеулер мен олардың жүйелерін шешу әдістері. Алдыңғы параграфта қарапайым тригонометриялық теңдеулерді шешу жолдарымен таныстық. Енді тригонометриялық теңдеулерді жалпы түрде шешудің әр түрлі әдістерін қарастырайық. I. Бір тригонометриялық функциямен берілген алгебралық теңдеулерге келетін тригонометриялық теңдеулер. 1 мысал. 2sin2x+3sinx-2=0 теңдеуінің шешімін табайық. Шешуі. Берілген теңдеу sіn х функциясына қатысты квадрат теңдеу болып табылады. Егер sіn х=и алмастыруын жасасак, онда 2u2+ Зu — 2 = 0 түріндегі алгебралык квадрат теңдеу аламыз, оның түбірлері и1=-2; и2 =1/2. Сонда берілген теңдеу sіn х функциясына катысты sіn х=-2 және sіn х=1/2 түріндегі қарапайым екі теңдеуге келеді. sіnх=-2 теңдеуінің шешімі жоқ, себебі теңдіктің оң жағы |-2| >1. sіn х=1/2,х=(-1)п•π/6 + πп, пεz. Енді табылған шешімінің берілген теңдеуді канағаттандыратынын тексерейік. Ол үшін х=π/6 -ны берілген теңдеуге коямыз. Сонда 2sin2π/6 + 3•sіnπ/6 - 2 = 2 • (1/2)2+ 3•(1/2) - 2 =(1/2) +(3/2)-2 = 0. Табылған шешім берілген теңдеуді қанағаттандырады. Жауабы: х= (-1)п•π/6 + πп, пεz 2-мысал. 3 соs2х = 7 соsх теңдеуін шешейік. Шешуі. Берілген теңдеудегі тригонометриялык функцияларды соs2х = 2соs2х — 1 формуласын пайдаланып, аргументтері бірдей тригонометриялық функцияға келтіреміз. 3(2соs2x- 1) = 7соsх немесе 6соs2х - 7 соsх - 3 = 0. соsх = и деп белгілеп, 6и2 — 7и - 3 = 0 теңдеуін аламыз. Сонда и1=3/2, и2=1/3.Алынған мәнді орнына койып, соsх = 3/2 ,соsх=-1/3 түріндегі қарапайым теңдеулер.Бірінші теңдеудің шешімі жоқ,екінші теңдеудің шешімі 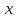 =arccos(-1/3)+2πп =arccos(-1/3)+2πп 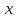 =±(π-arccos1/3)+2πп, пεZ =±(π-arccos1/3)+2πп, пεZЖауабы: 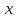 =±(π-arccos1/3)+2πп, пεZ =±(π-arccos1/3)+2πп, пεZ3-мысал.tgх + 3ctgx= 4 теңдеуін шешейік. Шешуі. tgx·ctgx= 1 формуласынан алынған tgx=1/ ctgx өрнегін берілген теңдеуге коямыз. Сонда 1/ ctgx +3ctgx = 4, 3ctgx 2х - 4ctgx+1=0. Енді ctgx=и алмастыруын енгізсек, З и 2 - 4 и + 1 = 0 түріндегі алгебралық теңдеу аламыз. Бұл тендеудің түбірлері и1=1/3, и2=1. Алынған мәндерді орнына қойсақ, ctgx =1/3 және ctgx = 1 түріндегі екі қарапайым теңдеуге келеміз. Бұл теңдеулердің шешімі сәйкесінше х =arcctg1/3+ πп, пεZ және х =arcctg1 + πп немесе х= π/4+ πп, пεZ Жауабы:arcctg1/3+πп, пεZ,π/4+ πп, пεZ ІІ.Тригонометриялық теңдеулерді түрлендіру жолымен шешілетін тригонометриялық теңдеулер. Мысалдар қарастырайық. -мысал. sіnх+ sіn2х + sіn3х = 0 теңдеуін шешейік. Шешуі.Берілген теңдеуді шешу үшін қосылғыштардың орнын ауыстырып , топтаймыз. Сонда (sіnх+sіn3х)+sіn2х=0 шыгады. Енді жақша ішіндегі өрнекке синустардың қосындысының формуласын, яғни sіnα+ sіnβ =2sіn(α+β)/2·соs(α-β)/2 пайдаланамыз.Сонда 2sіn(х+3х)/2·соs(х-3х)/2+ sіn2х = 0, 2sіn2х·соs(-х)+ sіn2х = 0,sіn2х·(2соsх+1)= 0, Берілген тендеу sіn2х= 0, соs х =-1/2 түріндегі екі қарапайым теңдеуге келеді. Бірінші теңдеудің шешімі: 2х = πп, х = π/2п, пεZ. Екінші теңдеудің шешімі: х = ±2π/3+2πп, пεZ. Жауабы: π/2п, пεZ; ±2π/3+2πп, пεZ. 5-мысал. соs4х • соs2х = соs5х· соsх теңдеуін шешейік. Шешуі. Тригонометриялық формулаларды қолданып, көбейтінді түрінде берілген өрнектерді қосындыға алмастырамыз: соs4х • соs2х = 1/2(соs6х+ соs2х), ал соs5х • соsх = 1/2(соs6х+ соs4х). Осыдан соs6х+соs2х-соs6х-соs4х=0 соs2х-соs4х=0 Енді косинустардың айырымының формуласын қолданып, 2sіn3х·sіnх=0 аламыз. Егер sіn3х =0 болса, онда 3х = πп, х = π/3п, пεZ. Егер sіnх = 0 болса, онда х = πп, х = πп, пεZ. Алынған шешімдерді біріктірсек, онда х = π/3п, пεZ шығады. Жауабы: х = π/3п,пεZ. Мысалдар қарастырайық. 8-мысал. 12 соsх - 5 sinx = 13 sin3x теңдеуін шешейік. Шешуі. Теңдіктің екі жағын мүшелеп 13-ке бөлеміз, себебі  . Сонда 12/13 соsх-5/13sinx=sin3x.Осы теңдіктен sinφ =12/13, cosφ=5/13 деп алсақ, онда sinφ•соsх+ соsφ•sinx= sin3x, мұндағы φ— қосымша бұрыш. Қосымша бұрыш 0 < φ<π/2 - аралығында өзгереді, себебі sinφ˃0, cosφ> 0. . Сонда 12/13 соsх-5/13sinx=sin3x.Осы теңдіктен sinφ =12/13, cosφ=5/13 деп алсақ, онда sinφ•соsх+ соsφ•sinx= sin3x, мұндағы φ— қосымша бұрыш. Қосымша бұрыш 0 < φ<π/2 - аралығында өзгереді, себебі sinφ˃0, cosφ> 0.sin(φ-x)- sin3x = 0 немесе sin3x+sin(x-φ) = 0, 2 sin(3х+х-φ)/2•соs(3х-х+φ)/2=0. Осыдан sin(2х -φ /2)= 0 және соs(х+φ /2)= 0 теңдеулеріне келеміз. sin(2х -φ /2)= 0; 2х -φ /2= πп; 2х=φ/2+πп, пεZ. х=φ /4+ πп/2, пεZ-бірінші теңдеудің шешімі. соs(х+φ /2)= 0, х+φ /2=π/2+πḳ, ḳεZ; х=π/2- φ/2+ πḳ, ḳεZ-екінші теңдеудің шешімі. Қосымша аргумент φ= arccos5/13теңдеуімен анықталса (себебі cosφ=5/13),онда x=1/4 arccos5/13+ πп/2, пεZ, х=π/2- 1/2 arccos5/13+ πḳ, ḳεZ. Егер қосымша аргумент sinφ =12/3 теңдігімен анықталса, ондаφ=arcsin12/13. Теңдеудің шешімі мына түрде беріледі: x=1/4 arcsin12/13+ πп/2, пεZ, х=π/2- 1/2 arcsin12/13+ πḳ, ḳεZ. VI. Тригонометриялық теңдеулер жүйесін шешу. Анықтама. Тригонометриялық теңдеуі бар жүйенітригонометриялық теңдеулер жүйесі деп атайды. Тригонометриялық теңдеулер жүйесін шешу алгебралық тендеулер жүйесін шешу әдістеріне негізделген, демек, ол алгебралық теңдеулер жүйесін шешу әдістерін тригонометриялық формулаларды түрлендірулер кезінде колдана білу мен тригонометриялық теңдеулерді шешу дағдысын меңгеруді қажет етеді. Тригонометриялық теңдеулер жүйесінің анықтамасы Қандай жүйені тригонометриялық теңдеулер жүйесі деп атаймыз? •Анықтама. Тригонометриялық теңдеуі бар жүйені тригонометриялық теңдеулер жүйесі деп аталады. Әр түрлі тригонометриялық теңдеулерді шешу алгебралық теңдеулерді шешу әдістеріне негізделіп шешіледі.  Теңдеулер жүйесін шешу әдістері       Жаңа айнымалыны енгізу әдісі Алгебралық қосу (азайту) әдісі Алмастыру әдісі Тригонометриялық теңдеулер жүйесін шешкенде осы әдістерді және тригонометриялық тепе-теңдіктер мен негізгі формулаларды қолданамыз. Әр түрлі тригонометриялық теңдеулер жүйесінін шешу әдістері І түрі. 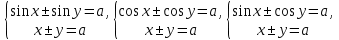 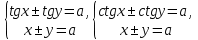 Бұндай түрдегі берілген теңдеулер жүйесін шешу үшін бірінші теңдеудегі қосындыны немесе айырымды көбейтінді түріне келтіреміз. •1-мысал. 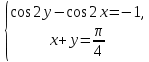 теңдеулер жүйесін шешейік. теңдеулер жүйесін шешейік.Шешуі: Бірінші теңдеудегі косинустардың айырымын көбейтінгдіге түрлендіру формуласын қолданамыз: 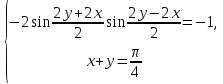 ⇒ ⇒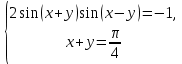 ⇒ ⇒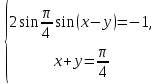 ⇒ ⇒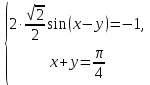 ⇒ ⇒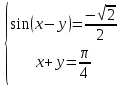 Алмастыру әдісі бойынша екінші теңдеудегі x-тіy арқылы өрнектеп, оны бірінші теңдеудегі x-тің орнына қоямыз: 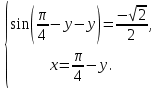 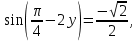 - 2y = - 2y = 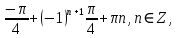 y = 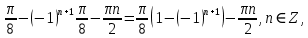 x = 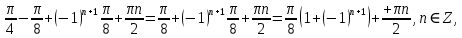 Егер n = 2kболса, онда х = 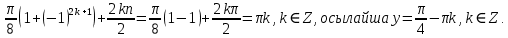 Егер n = 2k + 1 болса, онда х = 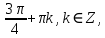 y= - y= - 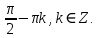 Жауабы: 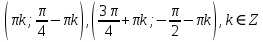 ІІ түрі. 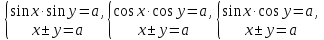 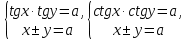 Бұл тригонометриялық теңдеулерді шешу үшін көбейтіндіні қосындыға түрлендіру формуласын қолданамыз. ІІІ түрі. 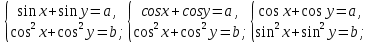 Бұндай теңдеулер жүйесін шешу үшінu = 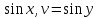 белгілеулерін белгілеулерін енгізіп, 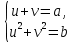 ⇒ ⇒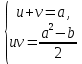 жүйесін аламыз. жүйесін аламыз.•3-мысал. 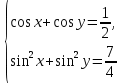 теңдеулер жүйесін шешейік. теңдеулер жүйесін шешейік.Шешуі:sin2x = 1 – cos2формуласын қолданып, 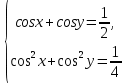 түріне келтіріп, u = түріне келтіріп, u =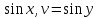 белгілеулерін енгіземіз. белгілеулерін енгіземіз.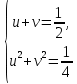 ⇒ ⇒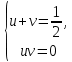 бұл теңдеуді шешуді өздерің орындаңдар. бұл теңдеуді шешуді өздерің орындаңдар.u1 = 0, v1= 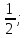 u2 = u2 = 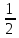 , v2 = 0. , v2 = 0.Табылған бұл мәндерді белгілеудегі u мен v-ның орнына қойып x пен у-тіңмәндерін табамыз: 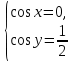 ⇒ ⇒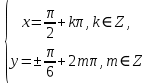 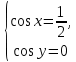 ⇒ ⇒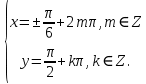 Жауабы: 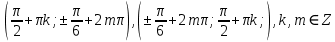 ІV түрі. 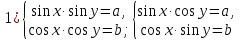 (1) (1)түріндегі теңдеулерді шешу үшін теңдеулерді бір-біріне қосып және азайту арқылы 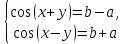 және және 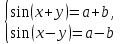 түріне келтіреміз. түріне келтіреміз.2) 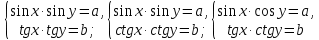 Бұл теңдеулерді шешу үшін бірінші теңдеуді екінші теңдеуге бөліп, (1)жүйенің түріне келтіреміз. 3) 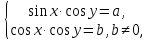 түріндегі жүйелерді шешу үшін оның бірінші теңдеуін екіншісіне бөліп, түріндегі жүйелерді шешу үшін оның бірінші теңдеуін екіншісіне бөліп, 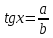 теңдеуінен х-тің мәнін тауып, оны теңдеуінен х-тің мәнін тауып, оныберілген жүйенің біреуіне қойып у-ті табуға болады. •4-мысал. 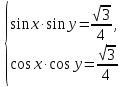 теңдеулер жүйесін шешейік. теңдеулер жүйесін шешейік.Шешуі: 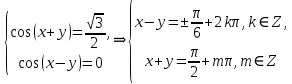 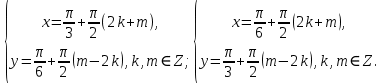 Жауабы:𝜋3+𝜋22𝑘+𝑚;𝜋6+ 𝜋2𝑚−2𝑘, 𝜋6+ 𝜋22𝑘+𝑚;𝜋3+𝜋2𝑚−2𝑘, 𝑘,𝑚∈𝑍. Мына кестені толтыра отырып сабақтың мазмұны бойынша қорытынды шығар.
Деңгейлік тапсырмалар: І деңгей тапсырмалары № 118.Тиімді тәсілді қолданып, жүйені шешіңдер: ә)______________________________________________________________ _________________________________________________________________ _________________________________________________________________ ІІ деңгей тапсырмалары № 127.a) 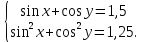 Нұсқау. Теңдеулер жүйесін шешудің ІІІ түрін және оқулықтағы 10-мысалды қолданып жүйені шешіңдер. _________________________________________________________________________________________________________________________________________________________________________________________________ ІІІ деңгей тапсырмалары № 135. б) 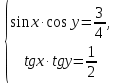 теңдеулер жүйесін шешіңдер. теңдеулер жүйесін шешіңдер.Нұсқау. Теңдеулер жүйесін шешудің ІV түрін, яғни бірінші теңдеуді екінші теңдеуге бөліп, (1)жүйенің түріне келтіріңдер. _______________________________________________________________________________________________________________________________ Жауабы: x = 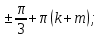 y = y = 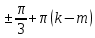 , , 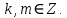 Оқулықпен жұмыс. Есеп шығару: №113; №122; №126; Үй тапсырмасы. §1.№117; №124; №127 ІҮ. Деңгейлік тапсырмалар(Сынып оқушылары 4 топқа бөлінген. Әр топтың топ басшылары бар. Әр оқушыға әр түрлі есептер беріледі,белгілі уақыт ішінде оқушылар есепті шығарып топ басшысына жұмыстарын өткізеді,осы сәтте топ басшысына есептің дұрыс жауабы беріледі.Ол өз тобын тексеріп,әр оқушының ұпайын анықтайды. Білімді бағалау парағына барлық оқушының ұпайы жазылып отырады) Мұнда әр оқушының білім деңгейі анықталады. А деңгейлі: Қарапайым тригонометриялық теңдеулерді шешіңіз: Мысалы: cosx= 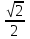 берілсін. берілсін.Мұндағы: 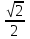 - -1< - -1<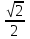 <1 аралығына тиісті екені белгілі, онда бұл теңдеудің шешімі мына түрде жазуға болады: х= <1 аралығына тиісті екені белгілі, онда бұл теңдеудің шешімі мына түрде жазуға болады: х=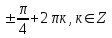  А деңгейлі Қарапайым тригонометриялық теңдеулерді шешіңіз: а) cosx= 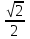 ә) sinx= ә) sinx=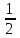 б) tgx= б) tgx=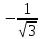 ( Оқытушы А деңгейлі есеп тақтада түсіндіреді. Аналогия әдісі бойынша оқушыларға А деңгейлі беріледі.) Тақтаға бір оқушы шығып, өзінің шығарған есебін барлығына түсіндіріп береді. В деңгейлі. Тригонометриялық теңдеулерді шешіңіз:(10 мин) Мысалы: 2сos( 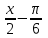 )= )=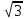 теңдеуі берілсін. Осы теңдеуді шешу жолдарын қарастырайық. Ол үшін теңдеуді сos( теңдеуі берілсін. Осы теңдеуді шешу жолдарын қарастырайық. Ол үшін теңдеуді сos(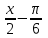 )= )=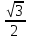 түріне келтіреміз. Осыдан: түріне келтіреміз. Осыдан: 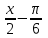 = =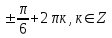 , , 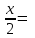 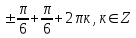 , х= , х= тең болады. тең болады. В деңгейлі Тригонометриялық теңдеулерді шешіңіз:а) 2сos( 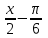 )= )=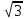 ә) 2sin( ә) 2sin(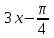 )= )=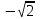 б) tg( б) tg(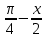 )= )=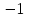 (Бұл деңгейдің есебі де түсіндіріліп,оқушыларға тапсырмалар таратылады.) Сергіту сәті: Жұмбақтар шешу; 1. Алды-артымыз шенсіз де, Жете алмайсың біздерге Сәуле менен кесінді, Шыққан тегін білсе де (Түзу) 2. Нәрселерді санағанда Керек ол бізге ауадай Айтыңдаршы бұл қандай сан, Жан- жағыңа қарамай? (Натурал сан) 3. Бойы да екі қарыс, сиып тұр 25 арыс (Сызғыш) 4. Бірдей санды бірнеше рет Көбейтуден тұрады Егер оны ықшамдасаң, Қандай атау болады? (Дәреже) С деңгейлі. Тригонометриялық теңдеулерді шешіңіз: (13 мин) Мысалы, 2sin2 x+sinx-1=0 теңдеуі берілген. Бұл теңдеуді шешу үшін sinx=y алмастыруын жасаймыз. Сонда: 2у2+у-1=0 теңдеуін аламыз. D=1+4*2=9. y1= 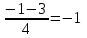 y2= y2=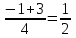 Бұдан: Бұдан:1. sinx=-1 x= - 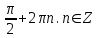 2. sin= 2. sin=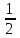 x=(-1)к x=(-1)к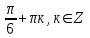 Сонда бастапқы берілген теңдеудің 2 шешімі бар екен: х1 = 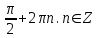 х2 =(-1)к 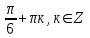 |

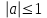 теңдеуінің шешімі неге тең? 15. sinx=а,
теңдеуінің шешімі неге тең? 15. sinx=а, 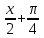 )+1= 0; 1. sin 2х -2cos2 х = 0;
)+1= 0; 1. sin 2х -2cos2 х = 0;