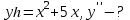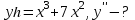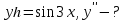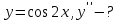|
|
Бірінші және екінші ретті туындылар және оларды есептеу. Бірінші жне екінші ретті туындылар жне оларды есептеу
Бірінші және екінші ретті туындылар және оларды есептеу
6.1 Айқындалған түрде берілген функциялардың жоғарғы ретті туындылары
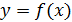 функциясының функциясының 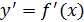 туындысы туындысы 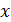 -тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер -тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер 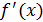 функциясы дифференциалданатын болса, онда оның туындысы екінші ретті туынды деп аталып, функциясы дифференциалданатын болса, онда оның туындысы екінші ретті туынды деп аталып, 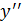 арқылы белгіленеді. Сонымен, арқылы белгіленеді. Сонымен, 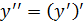 . Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып, . Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып, 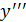 арқылы белгіленеді. Сонымен, арқылы белгіленеді. Сонымен, 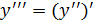 . n-ретті туынды деп . n-ретті туынды деп 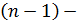 ретті туындыдан алынған туынды аталады: ретті туындыдан алынған туынды аталады:
|
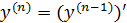 . .
|
(6.1)
|
Реті екіден жоғары туындылар жоғары ретті туындалар деп аталады.
6.2 Екінші ретті туындының механикалық мағынасы
 материалдық нүктесі S=f(t) заңы бойынша түзу сызық бойымен қозғалсын делік. Бізге белгілі болғандай материалдық нүктесі S=f(t) заңы бойынша түзу сызық бойымен қозғалсын делік. Бізге белгілі болғандай 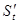 туындысы нүктенің сол уақыт мезетіндегі жылдамдығына тең туындысы нүктенің сол уақыт мезетіндегі жылдамдығына тең 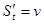 . Жолдың уақыт бойынша екінші туындысы нүктенің түзу сызықты қозғалысының үдеуінің шамасын анықтайтындығын, яғни . Жолдың уақыт бойынша екінші туындысы нүктенің түзу сызықты қозғалысының үдеуінің шамасын анықтайтындығын, яғни 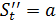 болатындығын көрсетейік. Нүктенің t уақыт мезетіндегі жылдамдығы v, ал болатындығын көрсетейік. Нүктенің t уақыт мезетіндегі жылдамдығы v, ал 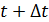 уақыт мезетінде жылдамдық уақыт мезетінде жылдамдық 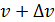 болсын делік, яғни болсын делік, яғни 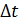 уақыт аралығында жылдамдық уақыт аралығында жылдамдық 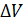 -ға өзгереді. -ға өзгереді. 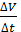 қатынасы қатынасы 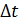 уақыты нүктенің қозғалысының орташа үдеуін өрнектейді. уақыты нүктенің қозғалысының орташа үдеуін өрнектейді. 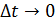 болғандағы осы қатынастың шегі М нүктесінің берілген уақыт мезетіндегі үдеуі деп аталып, а әрпі арқылы белгіленеді: болғандағы осы қатынастың шегі М нүктесінің берілген уақыт мезетіндегі үдеуі деп аталып, а әрпі арқылы белгіленеді: 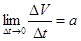 . Бірақ . Бірақ 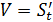 болғандықтан, болғандықтан, 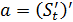 , яғни , яғни 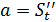 . .
6.3 Айқындалмаған түрде берілген функцияның жоғарғы ретті туындылары
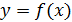 функциясы функциясы 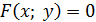 теңдеуі арқылы айқындалмаған түрде берілсін. Берілген теңдеуді теңдеуі арқылы айқындалмаған түрде берілсін. Берілген теңдеуді 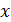 бойынша дифференциалдап, алынған теңдеуді y/ -ке қатысты шешсе, бірінші ретті туындыны табамыз. Бірінші туындыны x бойынша дифференциалдап, айқындалмаған функцияның екінші туындысын аламыз. Оның құрамына x, y, y/ кіреді. y/ -тың табылған мәнін екінші туындының өрнегіне қойсақ, y// -ты x пен y арқылы өрнектейміз. Тура осылай үшінші ретті, одан да басқа жоғары ретті туындыларды табамыз. бойынша дифференциалдап, алынған теңдеуді y/ -ке қатысты шешсе, бірінші ретті туындыны табамыз. Бірінші туындыны x бойынша дифференциалдап, айқындалмаған функцияның екінші туындысын аламыз. Оның құрамына x, y, y/ кіреді. y/ -тың табылған мәнін екінші туындының өрнегіне қойсақ, y// -ты x пен y арқылы өрнектейміз. Тура осылай үшінші ретті, одан да басқа жоғары ретті туындыларды табамыз.
6.4 Параметрлік түрде берілген функциялардың жоғарғы ретті туындылары
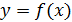 функциясы функциясы
|
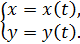
|
(6.2)
|
параметрлік теңдеуімен берілсін. 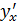 бірінші туындысы бірінші туындысы
|
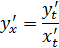
|
(6.3)
|
формуласы арқылы табылатыны бізге белгілі. Параметрлік түрде берілген функциядан екінші туындыcы
|
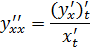
|
(6.4)
|
Тапсырмалар
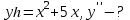
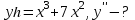
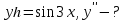
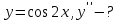
|
|
|
 Скачать 44.43 Kb.
Скачать 44.43 Kb.