|
|
Біртекті теңд жүйесі иргели шешмдер. Біртекті сызыты алгебралы тедеулер жйесі. Іргелі шешімдер жйесі
Біртекті сызықтық алгебралық теңдеулер жүйесі. Іргелі шешімдер жүйесі
 белгісізі бар белгісізі бар 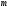 сызықты теңдеулер жүйесі берілсін. сызықты теңдеулер жүйесі берілсін.
 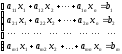
мұндағы 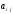 - жүйенің коэффициенттері, нақты сандар, - жүйенің коэффициенттері, нақты сандар, 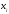 - белгісіз шамалар, - белгісіз шамалар, 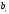 - бос мүшелер, - бос мүшелер, 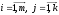 ., ., 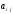 - коэффициенттері екі индекспен берілген, бірінші индексі - коэффициенттері екі индекспен берілген, бірінші индексі 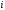 теңдеу нөмірін, ал екінші индекс теңдеу нөмірін, ал екінші индекс 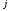 белгісіз нөмірін көрсетеді. белгісіз нөмірін көрсетеді. 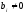 болса, онда жүйе біртекті емес жүйе деп аталады. Ал болса, онда жүйе біртекті емес жүйе деп аталады. Ал 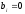 болса, онда жүйе біртекті жүйе деп аталады. болса, онда жүйе біртекті жүйе деп аталады.
Анықтама. Егер сызықты теңдеулер жүйесіндегі бос мүшелерінің кем дегенде біреуі нөлге тең болмаса, онда жүйені біртекті емес сызықты теңдеулер жүйесі деп, ал бос мүшелерінің бәрі нөлге тең болса, онда ол біртекті сызықты теңдеулер жүйесі деп аталады.
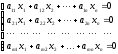
Жүйенің матрицалық түрде жазылуы: 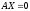 , ,
мұндағы:  - жүйе матрицасы, - жүйе матрицасы, 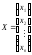 , , 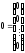
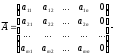 бұл матрица берілген жүйенің кеңейтілген матрицасы деп аталады. бұл матрица берілген жүйенің кеңейтілген матрицасы деп аталады.
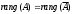 , яғни Кронекер-Капелли теоремасы бойынша біртекті жүйе әрқашанда үйлесімді және оның әрқашанда нөлдік шешімі бар: , яғни Кронекер-Капелли теоремасы бойынша біртекті жүйе әрқашанда үйлесімді және оның әрқашанда нөлдік шешімі бар: 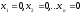
Егер біртекті теңдеулер жүйесінің анықтауышы нөлге тең болмаса, онда жүйенің бір ғана нөлдік шешімі болады.
Егер біртекті теңдеулер жүйесінің анықтауышы нөлге тең болса, онда жүйенің нөлдік емес шешімі болады.
Теорема. Біртекті теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін жүйенің рангісі жүйедегі белгісіздер санынан кем болуы қажетті және жеткілікті.
Теорема.  белгісізі бар белгісізі бар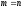 біртекті теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін жүйенің анықтауышы нөлге тең болуы қажетті әрі жеткілікті. біртекті теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін жүйенің анықтауышы нөлге тең болуы қажетті әрі жеткілікті.
Анықтама. Біртекті сызықты теңдеулер жүйесінің кез келген  сызықты тәуелсіз шешімі осы жүйенің іргелі шешімі деп аталады, мұндағы сызықты тәуелсіз шешімі осы жүйенің іргелі шешімі деп аталады, мұндағы  - жүйенің белгісіздер саны, - жүйенің белгісіздер саны,
 - матрица рангісі ( - матрица рангісі (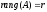 ). ).
Анықтама. Егер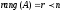 біртекті сызықты теңдеулер жүйесінің кез келген біртекті сызықты теңдеулер жүйесінің кез келген 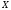 шешімінде шешімінде  тұрақты сан болса, онда ол шешім осы жүйенің жалпы шешімі деп аталады. тұрақты сан болса, онда ол шешім осы жүйенің жалпы шешімі деп аталады.
Мысал. 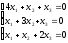
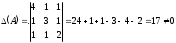 біртекті теңдеулер жүйесінің анықтауышы нөлге тең емес, олай болса жүйенің бір ғана нөлдік шешімі бар. біртекті теңдеулер жүйесінің анықтауышы нөлге тең емес, олай болса жүйенің бір ғана нөлдік шешімі бар. 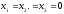
Мысал. 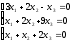
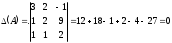 , жүйенің нөлден өзге шешімдері бар. , жүйенің нөлден өзге шешімдері бар.
Жүйенің рангісін табамыз. Үшінші ретті анықтауыш 0-тең болды, олай болса екінші ретті анықтауышты қарастырамыз.
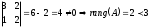 ,олай болса жүйенің шексіз көп шешімі бар. ,олай болса жүйенің шексіз көп шешімі бар.

миноры базистік деп аталады, коэффициенттері осы минордың элементтері болатын теңдеулерден тұратын жүйе құрамыз:
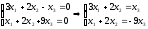
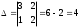
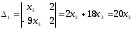
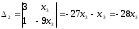
Крамер ережесін қолдансақ, 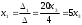 , , 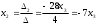 , , 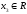 (жүйенің жалпы шешімі) (жүйенің жалпы шешімі)
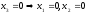
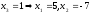
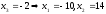
Жауабы: 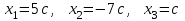
Егер 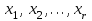 коэффициенттерінен құрылған анықтауыш нөлден өзгеше болса, онда коэффициенттерінен құрылған анықтауыш нөлден өзгеше болса, онда 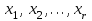 айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды.
Еркін айнымалылары нөлге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны 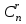 -ден артпайды. -ден артпайды.
Бірнеше мысал қарастырайық.
1-мысал. 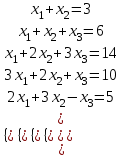
Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
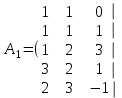 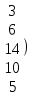 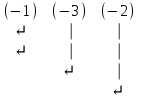 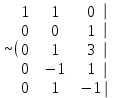 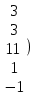 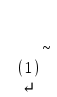
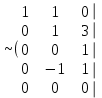 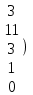 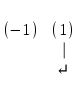 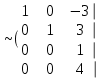 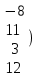 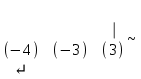
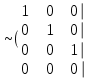 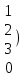 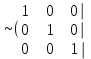 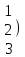 . .
Соңғы матрицаға сәйкес келетін жүйе жазайық:
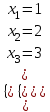
Сонымен жүйенің шешімі табылды: 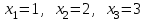
2-мысал. 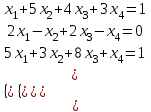
Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
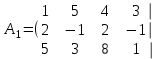 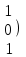 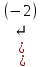 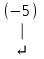 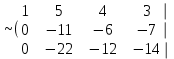 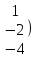 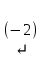
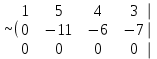 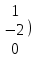 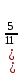 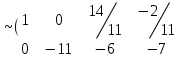 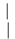 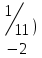
Соңғы матрицаға сәйкес келетін жүйе жазайық:
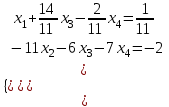
Осы жүйеден 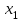 және және 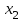 айнымалыларды табамыз: айнымалыларды табамыз:
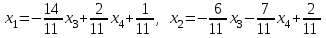
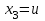 және және 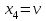 деп алсақ жүйе шешімі мынадай болады: деп алсақ жүйе шешімі мынадай болады:
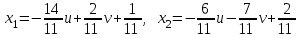 , , 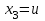 , , 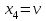 . .
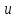 , ,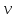 айнымалылардың орнына еркімізше сан беріп жүйенің сәйкес шешімін табамыз. Сонымен, берілген жүйенің шексіз көп шешімі бар екен. айнымалылардың орнына еркімізше сан беріп жүйенің сәйкес шешімін табамыз. Сонымен, берілген жүйенің шексіз көп шешімі бар екен.
ТЕРУ ФОРМУЛАСЫ
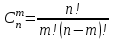
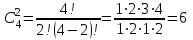
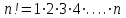
3-мысал. 2-мысалдағы жүйенің барлық базистік шешімдерін табу керек.
Шешуі. Матрица рангісі 2-ге тең екенін кеңейтілген матрицаға жүргізілген түрлендірулерден кейін көру қиын емес, сондықтан жүйедегі екі теңдеуді (мысалы, бастапқы екеуін) қарастырамыз:
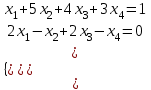
Олай болса базистік шешімдері 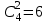 дан артпайды. Базистік айнымалылар ретінде мына айнымалылар жұбын алуға болады: дан артпайды. Базистік айнымалылар ретінде мына айнымалылар жұбын алуға болады:
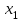 , ,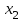 ; ; 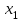 , ,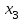 ; ; 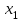 , ,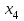 ; ; 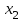 , ,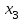 ; ; 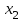 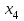 ; ; 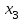 , ,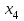 . .
Енді әрқайсысының базистік айнымалылар бола алатынын немесе бола алмайтынын білу үшін коэффициенттерінен құрылған анықтауыштарды есептейміз. Айталық 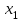 , ,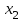 айнымалылар коэффициенттеріне құрылған анықтауыш айнымалылар коэффициенттеріне құрылған анықтауыш
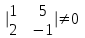 , олай болса бұлар базистік айнымалылар бола алады. Базистік шешімді табу үшін жүйедегі , олай болса бұлар базистік айнымалылар бола алады. Базистік шешімді табу үшін жүйедегі 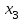 , ,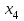 айнымалыларды нөлге теңестіреміз де жүйені мына түрде жазамыз: айнымалыларды нөлге теңестіреміз де жүйені мына түрде жазамыз:
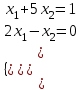
Бұл жүйенің шешімі: 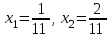 . .
Сонда бастапқы жүйенің бір базистік шешімі: 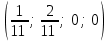 болады. болады.
Осы жолмен барлық 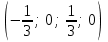 , , 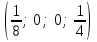 , , 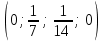 , , 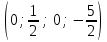 , , 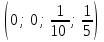 базистік шешімдерді табамыз. базистік шешімдерді табамыз.
4-мысал. Біртекті теңдеулер жүйесін шешейік.
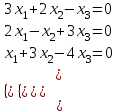
5-мысал.
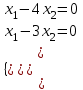
6-мысал. 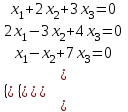
Шешуі. Біртекті жүйе әруақытта үйлесімді, себебі жүйенің 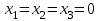 нолдік шешуі бар. Ендік нолдік емес шешулері бар жоқтығын анықтайық. нолдік шешуі бар. Ендік нолдік емес шешулері бар жоқтығын анықтайық.
Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
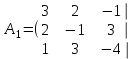 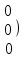 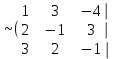 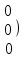 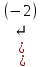 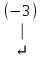 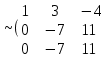  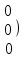 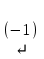
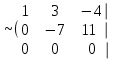 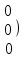 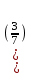 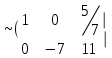 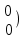
Соңғы матрицаға сәйкес келетін жүйе жазайық:
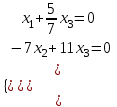
Осы жүйеден 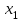 және және 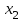 айнымалыларды табамыз: айнымалыларды табамыз:
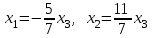 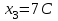 деп алсақ жүйе шешімі мынадай болады: деп алсақ жүйе шешімі мынадай болады:
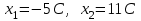 , , 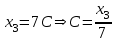 . .
Мысал. 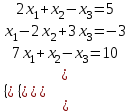 жүйесін Гаусс әдісімен шешу керек. жүйесін Гаусс әдісімен шешу керек.
Шешуі. Кеңейтілген матрицасын құрамыз:
А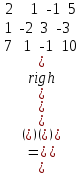 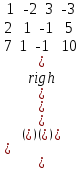
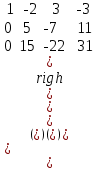
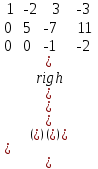
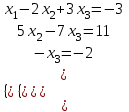 x1 = 1; x2 = 5; x3 = 2. x1 = 1; x2 = 5; x3 = 2. |
|
|
 Скачать 180.27 Kb.
Скачать 180.27 Kb.