Великая отечественная война для меня она. БойльМариотт заы. Газды траты температура кезінде арастырса, мндай шарттар изотермиялы
 Скачать 85.5 Kb.
|
|
Идеал газдар бағынатын заңдар әлдеқашан ашылған болатын. Бұл заңдардың барлығын да кинетикалық теория теңдеуінен шығарып алуға болады. Бойль-Мариотт заңы.Газды тұрақты температура кезінде қарастырсақ, мұндай шарттар изотермиялық деп аталады. Егер (10.9) теңдеуінде  деп алатын болсақ, онда теңдіктің оң жағының тұрақты болып шығатындығы анық, яғни  (10.11). Бұл теңдеуді изотерма теңдеуі деп атайды және ол Бойль-Мариотт заңының математикалық өрнегі болып табылады: газдың берілген массасы үшін тұрақты температура кезінде оның қысымы мен көлемінің көбейтіндісі тұрақты болып қалады.
Гей Люссак заңы. Енді газдың  қысымы тұрақты болып қалып, оның температурасы мен көлемі өзгеретін болсын. Мұндай шартты орындау үшін газды жылжымалы поршенмен жабылған цилиндрге ұстайық. Мұндай цилиндрдегі газдың температурасын өзгерткен кезде газдың қысымы өзгеріп, ол поршенді жылжытады да, газдың көлемі де өзгереді. Газ тепе-теңдік күйіне келген кезде газ қысымы бастапқы мәнін қабылдайды. (10.10) теңдеуінен көріп отырғандай, мұндай жағдайда газ көлемінің оның температурасына қатынасы өзгеріссіз қалады:  Изобара теңдеуідеп аталатын бұл теңдеу Гей-Люссак заңының математикалық өргені болып табылады; Изобара графигі  жоғарыдағы өрнектен көріп отырғанымыздай, координаттар басынан шығатын түзу болып табылады.Шарль заңы. Егер процесс кезінде газдың көлемі өзгеріссіз қалатын болса, онда газ күйі теңдеуінен  қатынасының өзгеріссіз қалатындығы шығады: (10.13) Теңдеу Изохора теңдеуі деп аталады және Шарль заңының мазмұны болып табылады.Авагадро заңы.Бұл заңды да газ күйінің теңдеуінен шығарып алуға болады: бірдей газ қысымы мен бірдей температура кезінде газдың бірдей көлемдерінде молекулалардың бірдей саны болады. Түрліше газдардың молекулаларының бірдей санының бірдей температуралары мен бірдей қысым кезінде бірдей көлем қабылдайтындығы шығады. Сондықтан 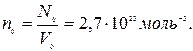 газдың молі берілген қысым мен температура кезінде бірдей көлем қабылдайды. Мысалға,  температура және  қысым кезінде газдың молінің көлемі  Осындай қалыпты жағдайлар деп аталатын кездерде  көлемдегі молекулалар саны  Бұл сан Лошмидт саны деп аталадОтынның жану энергиясын механикалық энергияға айналдырып беретін двигательдердің барлық түрлерін жылу двигательдері дейді. Жылу двигательдерінің барлығы да бір-бірімен бір бағытта тізбектеліп жалғасқан жеке процестермен тізбектелген, тұйықталған циклдер жасайды. Олардың барлығында да жұмыс денесі ретінде газ ( жанған отынның өнімі ) немесе бу пайдаланылады. Жұмыс денесін тұйықталған циклдер жасатуға жағдай тудыратын негізгі түйіндік элементтерге –қыздырғыш, энергияны түрлендіргіш механизм, суытқыш және жұмыс денесін, оның күйін қайта қалпына келтіруші механизмдер жүйесі жатады. Жылу двигательдерінің пайдалы әсер коэфициенті (ПӘК) істелінген  пайдалы жұмыстың қыздырғыштан алынған Q жылу мөлшеріне қатынасымен өлшенеді. Егер суытқышқа берілген жылу Q2 болса, онда пайдалы жұмыс  болады, ендеше:Жылу двигательдерінің ПӘК-нің ең жоғарғы мәні Карно циклі бойынша, яғни қыздырғыш пен суытқыштың абсолют температуралары арқылы анықталады.
Карно циклінің графигі бойынша істелінген жұмыс 1-2-3-4 контурының ауданына тең (27-сурет). Мұндағы:  1-2 процесс –изотермиялық ұлғаю; 2-3 процесс- адиабаталық ұлғаю; 3-4 процесс – изотермиялық сығылу; 4-1 процесс- адиабаталық сығылу; Жылу двигателінің түрлеріне бу турбиналы қондырғылар, іштен жану двигательдері (карбюраторлы, дизельді), реактивті, газтурбиналы двигательдер жатады. Кирхгроф ережелеріУикипедия — ашық энциклопедиясынан алынған мәлімет Jump to navigation Jump to search Кирхгофтың_бірінші_ережесі'>Кирхгофтың бірінші ережесі Тізбектерге есептеулер жүргізгенде Кирхгроф ережелерін пайдаланған ыңғайлы, олар Омзаңының күрделі емес жалпылануы болып табылады. Жалпы жағдайда тізбекте кем дегенде үш өткізгіш тоғысатын нүктелерді табуға болады. Мұндай нүктелер түйіндер деп аталады. Тізбектің бір элементін тастап шыұұан кез-келген зарядтың тізбек басқа бір элементіне келіп кіруі тиіс екені анық. Түйінде тоқтар тармақталады да, зарядтың сақталу заңынан, тоқтардың үзіліссіздік шарты шығады: түйінге кіріп жатқан тоқ күштерінің қосындысы, түйіннен шығып жатқан ток күшінің қосындысына тең: ∑ k i r i s ( I 1 ) = ∑ s h y g y s ( I 2 ) {\displaystyle \sum _{kiris}\left(I_{1}\right)=\sum _{shygys}\left(I_{2}\right)} Тоқтардың оң бағытын қалауымызша аламыз және оң бағытытта таралатын тоқ күшін I k {\displaystyle I_{k}}  деген белгілеу енгіземіз. Егер шешу кезінде қайсы бір I k {\displaystyle I_{k}} тоқ үшін теріс мән шықса, онда бұл берілген бөлікте тоқ қабылданған бағытқа қарама - қарсы қозғалады дегенді білдіреді. ∑ k i r i s ( I 1 ) = ∑ s h y g y s ( I 2 ) {\displaystyle \sum _{kiris}\left(I_{1}\right)=\sum _{shygys}\left(I_{2}\right)} қатынасы Кирхгрофтың бірінші ережесі деп аталады. Кирхгофтың екінші ережесі Берілген тізбекте бөліп қарастыруға болатын кез келген тұйықталған контурларға арналған: кез келген тұйықталған контурда кедергілерді кернеудің түсулерінің қосындысы осы контурдағы ЭҚК- тердің қосындысына тең болады. ∑ ( ϵ 1 ) = ∑ ( ϵ 2 ) {\displaystyle \sum _{}\left(\epsilon _{1}\right)=\sum _{}\left(\epsilon _{2}\right)} Егер берілген бөлікте контурды айналып өту бағыты токтың оң бағытымен бағыттас болса, онда ток көзінің ішкі кедергісіндегі және өткізгіштердегі кернеудің тусуі оң деп есептеледі. Егер ток көзін айналып өту бағыты теріс полюстен басталып оң полюсте аяқталатын болса, онда ЭҚК-і оң таңбамен алынады. Ток көзін оң полюстен бастап теріс полюске қарай айналып өтетін болса, онда ЭҚК-і теріс таңбамен алынады.[1] Мысалы 9,8 суретте көрсетілген сұлба үшін: А түйінінде: I 1 = I 3 + I 5 {\displaystyle I_{1}=I_{3}+I_{5}} С түйінінде: I 1 = I 2 + I 4 {\displaystyle I_{1}=I_{2}+I_{4}} М түйінінде: I 4 + I 6 = I 3 {\displaystyle I_{4}+I_{6}=I_{3}} BCKMOAB (сағат тілі бағытымен айналып өту) контуры үшін: ϵ 1 − ϵ 2 + ϵ 3 = I 1 r 1 + I 2 r 2 + I 3 r 3 {\displaystyle \epsilon _{1}-\epsilon _{2}+\epsilon _{3}=I_{1}r_{1}+I_{2}r_{2}+I_{3}r_{3}} CDEMC контуры үшін: ϵ 4 + ϵ 2 = I 4 r 4 − I 6 R 3 − I 2 r 2 {\displaystyle \epsilon _{4}+\epsilon _{2}=I_{4}r_{4}-I_{6}R_{3}-I_{2}r_{2}} Магнит өрісінің негізгі қасиеттері: Магнит өрісін магниттелген денелер, тогы бар өткізгіштер және қозғалыстағы зарядталған денелер тудырады; Токтардың өзара әсерi. Бұранда және сол қол ережесi.Магнит индукциясы. Магнит өрiсi Қозғалмайтын электр зарядтары электр өрiсiн туғызады, қозғалатын зарядтар басқа өрiс – магнит өрiсiн туғызады. Магнит индукциясы векторының модулi магнит өрiсi тарапынан тогы бар өткiзгiштiң бiр бөлiгiне әсер ететiн максималды күштiң ток күшiнiң сол бөлiк ұзындығына көбейтiндiсiнiң қатынасына тең: 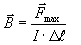 СИ жүйесінде Магнит индукциясының бірлігі ретінде В-ның өлшем бірлігі ретінде ұзындығы 1 м өткізгіштен 1 А ток өтіп тұрған кезде оған 1 Н күшпен әсер ететін магнит өрісінің индукциясының мәні алынады. Оны 1 Тесла (Тл) деп белгілейді, яғни 1 Тл=1 Н/ (А*м). Жоғарыдағы (1.1) өрнегi магнит өрiсiндегi тогы бар өткiзгiш элементiне әсер ететiн күштi анықтайтын Ампер заңының негiзiнде жазылған. Жоғарыдағы Осы құбылысты зерттеген француз ғалымы Андре Ампердiң құрметiне осылай аталған бұл заң бойынша Индукциясы В-ға тең бiртектi магнит өрiсiне орналасқан, бойынан I тогы өтiп жатқан өткiзгiштiң Δℓ элементiне әсер ететiн күштiң модулi мынаған тең: F=B·I·Δℓ·sinα мұндағы α - индукция векторы  мен өткiзгiштегi ток бағыты арасындағы бұрыш. | ||||||||
