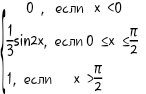15-17 типовая 4 симестр. Бросаются одновременно две игральные кости. Найти вероятность события, сумма выпавших очков 8
 Скачать 444 Kb. Скачать 444 Kb.
|
|
Из всей выпускаемой заводом продукции 95% составляет стандартные изделия. Наугад отобраны 6 деталей. Пусть Х – число стандартных деталей среди шести отобранных. Найдите дисперсию. Распределение случайной величины Х имеет вид :
И распределение величины У :
Найдите Д(Х) и Д(У) .
2.
3.
Найдите M(
Найти 20. Х случайная величина принимает возможные значения 21. Испытывается сооружение состоящее из четырех независимо работающих приборов. Выход из строя приборов соответственно равны 22. Найти дисперсию, если в каждом из 100 взаимно независимых испытаниях, событие происходит с одинаковой вероятностью 23. Х случайная величина задана законом распределения :
Найти среднее квадратическое отклонение 24. . Х случайная величина задана законом распределения :
Найти среднее квадратическое отклонение 25. . Х случайная величина задана законом распределения
Найти среднее квадратическое отклонение З а д а н и е 30 Случайная величина Х задана функцией распределения F(X). Найти среднее квадратическое отклонение
F(X) = 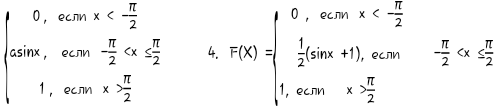
11. F(X)= 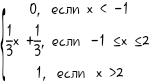 13. F(X)=  14. F(X)= 14. F(X)= 15. F(X) = 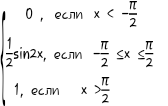 16. F(X) = 16. F(X) = 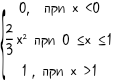 17. F(X) = 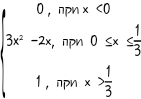 18. F(X) = 18. F(X) = 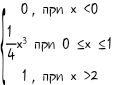
23. F(X) =  24. F(X) = 24. F(X) = 25. F(X) = 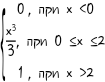 З а д а н и е 31 Известны математическое ожидание а и среднее квадратическое отклонение
З а д а н и е 32 Проведены опыты. Получили следующие данные. Составить вариационный ряд. Построить полигон и гистограмму частот. Найти 1. 13,1 12,8 13,5 13,0 12,6 13,2 13,0 13,8 13,1 12,9 12,7 13,2 13,1 12,8 12,3 13,0 13,1 13,2 13,0 13,4 13,3 13,0 12,9 12,5 13,1 12,7 13,3 13,1 12,0 13,1 13,1 12,8 13,5 13,0 12,6 13,2 13,0 12,8 13,1 13,5 12,9 13,4 13,1 12,7 13,3 13,1 12,9 12,6 13,1 12,8 |

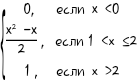 2. F(X) =
2. F(X) = 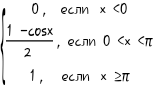
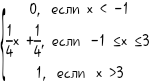 6. F(X)=
6. F(X)=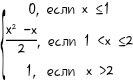
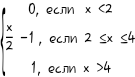 8. F(X)=
8. F(X)=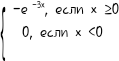
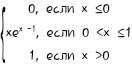 10. F(X)=
10. F(X)=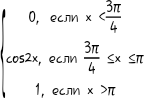
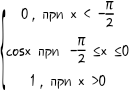 20. F(X) =
20. F(X) = 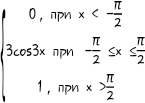
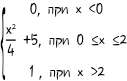 22. . F(X) =
22. . F(X) =