Отчет по лабе 4(сети). Цель работы исследовать сумму двух простейших потоков и определить характеристики результирующего потока. Ход работы
 Скачать 84.67 Kb.
|
|
Цель работы: исследовать сумму двух простейших потоков и определить характеристики результирующего потока. Ход работы: В данной лабораторной работе случайный поток задается последовательностью промежутков времени между вызывающими моментами методом Монте Карло.  Исходя из программы, написанной в ходе 3 лабораторной работы смоделируем два случайных потока и выведем так же поток, получившийся в ходе суммирования этих двух потоков:Построим график данных потоков используя библиотеку matplotlib: 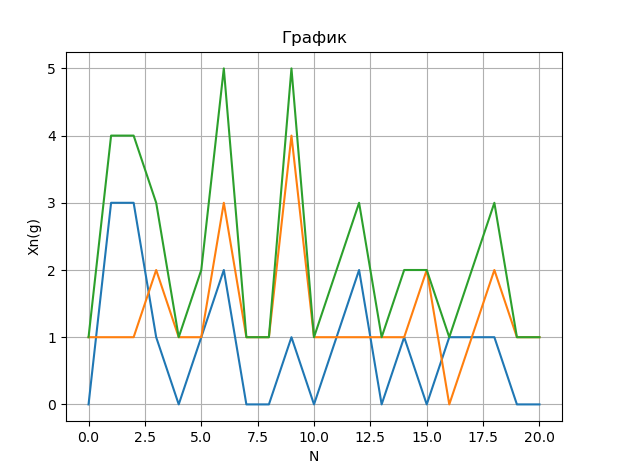 Выведем модельную интенсивность и сравним ее с суммой интенсивностей двух смоделериванных потоков:  Можено увидеть, что интенсивности немного различаются из за того, что смоделированные потоки не являются идеальными. Расчитаем остальные характеристики: 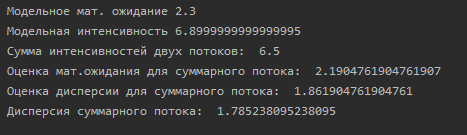 Оценка мат. ожидания примерно равна модельному мат.ожиданию, что говорит нам о приемлимости смоделированного суммарного потока. Оценка дисперсии так же примерно равна дисперсии потока, что так же позволяем нам сделать вывод о приемлимости потока. Код: import random, math, csv import matplotlib.pyplot as plt def potok(l): r = [] T = [] t = [] t.append(0) r.append(0) T.append(0) x = 0.1 math.log(x) for i in range(1,1000): r.append(random.random()) st = float(-math.log(r[i])*(1/l)) T.append(st) st = 0 for j in range(i+1): st += T[j] t.append(st) if t[i] >= 12: break g = (12 - 5)/21 q = 0 t2 = 5 for i in range(len(t)): if t[i] >= 5: q = i break Xn = [] Xn.append("Xn(g)") for i in range(21): count = 0 t1 = t2 t2 += g for j in range(len(t)): if t[j] >= t1 and t[j] <= t2: count +=1 Xn.append(count) print(Xn) return Xn def int(Xn): g = (12 - 5) / 21 k = max(Xn) Xn2 = [] nk = [] nk.append(" nk ") Xn2.append("Xn(g)") for i in range(k + 1): count = 0 Xn2.append(i) for j in range(len(Xn)): if Xn[j] == i: count += 1 nk.append(count) nk.pop(0) Xn2.pop(0) a = 0 for i in range(len(Xn2)): a += (Xn2[i] * nk[i]) a = a / 20 print("Модельное мат. ожидание " + str(a)) l = a / g print("Модельная интенсивность " + str(l)) return a,l N = [] N.append(" N ") for i in range(21): count = 0 N.append(i) print("Первая таблица") print(N) Xn1 = potok(9/4) Xn2 = potok(17/4) Xns = [] Xn1.pop(0) Xn2.pop(0) N.pop(0) Xns.append('x1+x2') for i in range(len(Xn1)): Xns.append(Xn1[i]+Xn2[i]) print(Xns) Xns.pop(0) a,l = int(Xns) print("Сумма интенсивностей двух потоков: ", (9/4)+(17/4)) Dx_ = 0 Mx_ = 0 Dx = 0 Mx_ = sum(Xns)/len(Xns) print("Оценка мат.ожидания для суммарного потока: ", Mx_) for i in range(len(Xns)): Dx_ += math.pow(Xns[i],2) Dx_ = Dx_/len(Xns) - math.pow(Mx_,2) print("Оценка дисперсии для суммарного потока: ", len(Xns)/(len(Xns)-1)*Dx_) for i in range(len(Xns)): Dx += math.pow(Xns[i]-a,2) Dx = Dx/len(Xns) print("Дисперсия суммарного потока: ", Dx) x = N y1 = Xn1 y2 = Xn2 y3 = Xns plt.title("График") plt.xlabel("N") plt.ylabel("Xn(g)") plt.plot(x, y1, x, y2, x, y3) plt.grid(True) plt.show() Вывод: в ходе данной лабораторной работы было смоделированно два потока и найден суммарный поток. Были найдены его числовые характеристики, которые свидетельствовали о том, что данный поток можно считать приемлимым. Модельная интенсивность суммарного потока примерно равна сумме интенсивностей двух смоделированных потоков, погрешность очень маленькая и роли не играет. |