Вариант №19.
Цель работы:
Изучение методов определения основных показателей надежности изделий на основе экспериментальных данных; разработка программного обеспечения обработки статистических данных по отказам изделий в процессе испытаний на надёжность или в процессе их эксплуатации.
Рабочие формулы:
2.1. Статистическая оценка интенсивности отказов, соответствующая каждому i-му интервалу времени, вычисляется по формуле:
 , , 
|
|
2.2. Общее числа отказов наблюдаемых изделий в интервале времени (0, ) вычисляется с помощью соотношения вида: ) вычисляется с помощью соотношения вида:
2.3. Статистическая оценка плотности распределения отказов (частота отказов) определяется как
 , , 
|
|
2.4. Статистическая оценка функции надежности изделия (вероятности безотказной работы) вычисляется как
 , ,  , ,
|
|
где 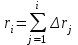 - число объектов, отказавших в интервале времени (0, - число объектов, отказавших в интервале времени (0, ). ).
2.5. Для проверки правильности определения оценок показателей надежности используется связь между показателями (t), p(t) и α(t) вида:
 , , 
|
|
2.6. Также надёжность характеризует средняя наработка на отказ. Статистическая оценка такого показателя имеет вид:
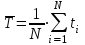
Начальные данные:
Вариант №19
518,63
|
265,05
|
584,06
|
688,48
|
508,93
|
269,53
|
96,95
|
904,35
|
998,56
|
952,23
|
1055,55
|
424,90
|
185,65
|
513,64
|
931,58
|
630,15
|
553,41
|
559,52
|
552,41
|
565,66
|
1625,92
|
509,55
|
518,99
|
629,68
|
505,55
|
545,06
|
663,25
|
360,90
|
680,13
|
936,45
|
215,51
|
945,80
|
1062,93
|
30,55
|
312,64
|
56,35
|
459,95
|
509,01
|
603,94
|
845,13
|
569,26
|
294,00
|
580,49
|
893,31
|
438,84
|
925,46
|
901,56
|
595,82
|
513,55
|
865,85
|
2,54
|
388,89
|
353,89
|
535,54
|
532,06
|
865,64
|
1211,25
|
901,13
|
450,00
|
595,60
|
505,55
|
661,32
|
514,51
|
352,05
|
622,35
|
538,09
|
539,83
|
431,53
|
1468,56
|
465,38
|
693,63
|
592,10
|
663,09
|
918,65
|
564,55
|
401,11
|
550,93
|
112,68
|
919,56
|
464,46
|
505,26
|
638,50
|
692,36
|
233,26
|
383,54
|
151,58
|
1458,88
|
511,41
|
316,24
|
1058,54
|
653,24
|
1032,35
|
1026,10
|
1012,63
|
480,89
|
669,00
|
406,29
|
955,86
|
1021,82
|
81568
|
Подготовка данных к работе:
4.1. Упорядочить данные в таблице от tmin до tmax:
2,54
|
30,55
|
56,35
|
96,95
|
112,68
|
151,58
|
185,65
|
215,51
|
233,26
|
265,05
|
269,53
|
294,00
|
312,64
|
316,24
|
352,05
|
353,89
|
360,90
|
383,54
|
388,89
|
401,11
|
406,29
|
424,90
|
431,53
|
438,84
|
450,00
|
459,95
|
464,46
|
465,38
|
480,89
|
505,26
|
505,55
|
505,55
|
508,93
|
509,01
|
509,55
|
511,41
|
513,55
|
513,64
|
514,51
|
518,63
|
518,99
|
532,06
|
535,54
|
538,09
|
539,83
|
545,06
|
550,93
|
552,41
|
553,41
|
559,52
|
564,55
|
565,66
|
569,26
|
580,49
|
584,06
|
592,10
|
595,60
|
595,82
|
603,94
|
622,35
|
629,68
|
630,15
|
638,50
|
653,24
|
661,32
|
663,09
|
663,25
|
669,00
|
680,13
|
688,48
|
692,36
|
693,63
|
815,68
|
845,13
|
865,64
|
865,85
|
893,31
|
901,13
|
901,56
|
904,35
|
918,65
|
919,56
|
925,46
|
931,58
|
936,45
|
945,80
|
952,23
|
955,86
|
998,56
|
1012,63
|
1021,82
|
1026,10
|
1032,35
|
1055,55
|
1058,54
|
1062,93
|
1211,25
|
1458,88
|
1468,56
|
1625,92
|
4.2. Выбранные интервалы времени:
∆t =  , n=30; 40; 50 , n=30; 40; 50
tmax, ч
|
n
|
∆t
|
1625,92
|
30
|
54,19
|
1625,92
|
40
|
40,64
|
1625,92
|
50
|
32,52
|
Результаты расчётов:
Для n = 30:
Интервалы
|
Кол-во отказов
|
Интенсивность отказов
|
Плотность распределения
|
Функция надёжности
|
Контроль
|
(ti, ti+1)
|
∆ri
|
λ*i
|
α*i
|
p*i
|
λ*I p*i-α*I = 0
|
0
|
54,19
|
0
|
0
|
0
|
1
|
0
|
54,19
|
108,38
|
3
|
0,000210
|
0,0002039
|
0,97
|
0
|
108,38
|
162,57
|
4
|
0,000189
|
0,0001812
|
0,93
|
-0,0000057
|
162,57
|
216,76
|
4
|
0,000142
|
0,0001359
|
0,91
|
-0,0000071
|
216,76
|
270,95
|
3
|
0,000084
|
0,0000816
|
0,86
|
-0,0000092
|
270,95
|
325,14
|
6
|
0,000145
|
0,0001359
|
0,8
|
-0,0000202
|
325,14
|
379,33
|
7
|
0,000146
|
0,0001359
|
0,73
|
-0,0000292
|
379,33
|
433,52
|
4
|
0,000071
|
0,0000680
|
0,69
|
-0,0000191
|
433,52
|
487,71
|
5
|
0,000079
|
0,0000755
|
0,64
|
-0,0000246
|
487,71
|
541,9
|
6
|
0,000087
|
0,0000816
|
0,58
|
-0,0000312
|
541,9
|
596,09
|
9
|
0,000122
|
0,0001112
|
0,49
|
-0,0000513
|
596,09
|
650,28
|
6
|
0,000072
|
0,0000680
|
0,43
|
-0,0000369
|
650,28
|
704,47
|
2
|
0,000021
|
0,0000209
|
0,41
|
-0,0000122
|
704,47
|
758,66
|
3
|
0,000030
|
0,0000291
|
0,38
|
-0,0000177
|
758,66
|
812,85
|
4
|
0,000038
|
0,0000362
|
0,34
|
-0,0000234
|
812,85
|
867,04
|
5
|
0,000045
|
0,0000425
|
0,29
|
-0,0000295
|
867,04
|
921,23
|
7
|
0,000060
|
0,0000560
|
0,22
|
-0,0000427
|
921,23
|
975,42
|
9
|
0,000075
|
0,0000680
|
0,13
|
-0,0000583
|
975,42
|
1029,61
|
4
|
0,000030
|
0,0000286
|
0,09
|
-0,0000259
|
1029,61
|
1083,8
|
3
|
0,000021
|
0,0000204
|
0,06
|
-0,0000191
|
1083,8
|
1137,99
|
2
|
0,000013
|
0,0000129
|
0,04
|
-0,0000124
|
1137,99
|
1192,18
|
2
|
0,000013
|
0,0000124
|
0,02
|
-0,0000121
|
1192,18
|
1246,37
|
1
|
0,000006
|
0,0000059
|
0,01
|
-0,0000059
|
1246,37
|
1300,56
|
0
|
0
|
0
|
0,01
|
0
|
1300,56
|
1354,75
|
0
|
0
|
0
|
0,01
|
0
|
1354,75
|
1408,94
|
0
|
0
|
0
|
0,01
|
0
|
1408,94
|
1463,13
|
0
|
0
|
0
|
0,01
|
0
|
1463,13
|
1517,32
|
0
|
0
|
0
|
0,01
|
0
|
1517,31
|
1571,51
|
0
|
0
|
0
|
0,01
|
0
|
1571,51
|
1625,7
|
1
|
0,000005
|
0,0000045
|
0
|
-0,0000045
|
Средняя наработка на отказ  = 900,48 (ч) = 900,48 (ч)
Для n = 40:
надежность изделие интенсивность вероятность
Интервалы
|
Кол-во отказов
|
Интенсивность отказов
|
Плотность распределения
|
Функция надёжности
|
Контроль
|
(ti, ti+1)
|
∆ri
|
λ*i
|
α*i
|
p*i
|
λ*I p*i-α*I = 0
|
0
|
|
0
|
0
|
0,0000000
|
1
|
0
|
|
|
4
|
0,000378
|
0,0003625
|
0,96
|
0
|
|
|
0
|
0
|
0,0000000
|
0,96
|
0
|
165,51
|
|
0
|
0
|
0,0000000
|
0,96
|
0
|
220,68
|
275,85
|
2
|
0,000074
|
0,0000725
|
0,94
|
-0,0000030
|
275,85
|
331,02
|
4
|
0,000126
|
0,0001208
|
0,9
|
-0,0000076
|
331,02
|
386,19
|
8
|
0,000225
|
0,0002072
|
0,82
|
-0,0000225
|
386,19
|
441,36
|
0
|
0
|
0,0000000
|
0,82
|
0,0000000
|
441,36
|
496,53
|
3
|
0,000062
|
0,0000604
|
0,79
|
-0,0000112
|
496,53
|
551,7
|
3
|
0,000056
|
0,0000544
|
0,76
|
-0,0000118
|
551,7
|
606,87
|
4
|
0,000069
|
0,0000659
|
0,72
|
-0,0000165
|
606,87
|
662,04
|
2
|
0,000031
|
0,0000302
|
0,7
|
-0,0000086
|
662,04
|
717,21
|
9
|
0,000138
|
0,0001255
|
0,61
|
-0,0000414
|
717,21
|
772,38
|
5
|
0,000068
|
0,0000647
|
0,56
|
-0,0000266
|
772,38
|
827,55
|
3
|
0,000037
|
0,0000363
|
0,53
|
-0,0000164
|
827,55
|
882,72
|
4
|
0,000047
|
0,0000453
|
0,49
|
-0,0000222
|
882,72
|
937,89
|
6
|
0,000068
|
0,0000640
|
0,43
|
-0,0000347
|
937,89
|
993,06
|
4
|
0,000042
|
0,0000403
|
0,39
|
-0,0000239
|
993,06
|
1048,23
|
2
|
0,000019
|
0,0000191
|
0,37
|
-0,0000119
|
1048,23
|
1103,4
|
4
|
0,000038
|
0,0000363
|
0,33
|
-0,0000238
|
1103,4
|
1158,57
|
3
|
0,000027
|
0,0000259
|
0,3
|
-0,0000179
|
1158,57
|
1213,74
|
3
|
0,000025
|
0,0000247
|
0,27
|
-0,0000178
|
1213,74
|
1268,91
|
3
|
0,000024
|
0,0000236
|
0,24
|
-0,0000178
|
1268,91
|
1324,08
|
1
|
0,000008
|
0,0000076
|
0,23
|
-0,0000058
|
1324,08
|
1379,25
|
2
|
0,000015
|
0,0000145
|
0,21
|
-0,0000114
|
1379,25
|
1434,42
|
2
|
0,000014
|
0,0000139
|
0,19
|
-0,0000112
|
1434,42
|
1489,59
|
3
|
0,000021
|
0,0000201
|
0,16
|
-0,0000168
|
1489,59
|
1544,76
|
2
|
0,000013
|
0,0000129
|
0,14
|
-0,0000111
|
1544,76
|
1599,93
|
1
|
0,000006
|
0,0000063
|
0,13
|
-0,0000054
|
1599,93
|
1655,1
|
3
|
0,000019
|
0,0000181
|
0,1
|
-0,0000163
|
1655,1
|
1710,27
|
3
|
0,000018
|
0,0000175
|
0,07
|
-0,0000163
|
1710,27
|
1765,44
|
3
|
0,000018
|
0,0000170
|
0,04
|
-0,0000163
|
1765,44
|
1820,61
|
3
|
0,000017
|
0,0000165
|
0,01
|
-0,0000163
|
1820,61
|
1875,78
|
0
|
0
|
0,0000000
|
0,01
|
0
|
1875,78
|
1930,95
|
0
|
0
|
0,0000000
|
0,01
|
0
|
1930,95
|
1986,12
|
0
|
0
|
0,0000000
|
0,01
|
0
|
1986,12
|
2041,29
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2041,29
|
2096,46
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2096,46
|
2151,63
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2151,63
|
2206,8
|
1
|
0,000005
|
0,0000045
|
0
|
-0,0000045
|
Средняя наработка на отказ  = 900,48 (ч) = 900,48 (ч)
Для n = 50:
Интервалы
|
Кол-во отказов
|
Интенсивность отказов
|
Плотность распределения
|
Функция надёжности
|
Контроль
|
(ti, ti+1)
|
∆ri
|
λ*i
|
α*i
|
p*i
|
λ*I p*i-α*I = 0
|
0
|
44,14
|
0
|
0
|
0,0000000
|
1
|
0
|
44,14
|
88,28
|
2
|
0,000231
|
0,0002266
|
0,98
|
0
|
88,28
|
132,42
|
1
|
0,000076
|
0,0000755
|
0,97
|
-0,0000015
|
132,42
|
176,56
|
1
|
0,000057
|
0,0000566
|
0,96
|
-0,0000017
|
176,56
|
220,7
|
1
|
0,000046
|
0,0000453
|
0,95
|
-0,0000018
|
220,7
|
264,84
|
0
|
0
|
0,0000000
|
0,95
|
0,0000000
|
264,84
|
308,98
|
11
|
0,000400
|
0,0003560
|
0,84
|
-0,0000200
|
308,98
|
353,12
|
2
|
0,000058
|
0,0000566
|
0,82
|
-0,0000092
|
353,12
|
397,26
|
3
|
0,000078
|
0,0000755
|
0,79
|
-0,0000140
|
397,26
|
441,4
|
0
|
0
|
0,0000000
|
0,79
|
0,0000000
|
441,4
|
485,54
|
1
|
0,000021
|
0,0000206
|
0,78
|
-0,0000044
|
485,54
|
529,68
|
4
|
0,000079
|
0,0000755
|
0,74
|
-0,0000173
|
529,68
|
573,82
|
4
|
0,000073
|
0,0000697
|
0,7
|
-0,0000189
|
573,82
|
617,96
|
1
|
0,000016
|
0,0000162
|
0,69
|
-0,0000049
|
617,96
|
662,1
|
3
|
0,000047
|
0,0000453
|
0,66
|
-0,0000145
|
662,1
|
706,24
|
11
|
0,000175
|
0,0001558
|
0,55
|
-0,0000595
|
706,24
|
750,38
|
1
|
0,000013
|
0,0000133
|
0,54
|
-0,0000061
|
750,38
|
794,52
|
2
|
0,000026
|
0,0000252
|
0,52
|
-0,0000118
|
794,52
|
838,66
|
2
|
0,000024
|
0,0000238
|
0,5
|
-0,0000117
|
838,66
|
882,8
|
3
|
0,000035
|
0,0000340
|
0,47
|
-0,0000175
|
882,8
|
926,94
|
1
|
0,000011
|
0,0000108
|
0,46
|
-0,0000058
|
926,94
|
971,08
|
6
|
0,000066
|
0,0000618
|
0,4
|
-0,0000355
|
971,08
|
1015,22
|
0
|
0
|
0,0000000
|
0,4
|
0
|
1015,22
|
1059,36
|
0
|
0
|
0,0000000
|
0,4
|
0
|
1059,36
|
1103,5
|
1
|
0,000009
|
0,0000091
|
0,39
|
-0,0000055
|
1103,5
|
1147,64
|
7
|
0,000066
|
0,0000610
|
0,32
|
-0,0000400
|
1147,64
|
1191,78
|
2
|
0,000017
|
0,0000168
|
0,3
|
-0,0000116
|
1191,78
|
1235,92
|
1
|
0,000008
|
0,0000081
|
0,29
|
-0,0000057
|
1235,92
|
1280,06
|
1
|
0,000008
|
0,0000078
|
0,28
|
-0,0000056
|
1280,06
|
1324,2
|
3
|
0,000023
|
0,0000227
|
0,25
|
-0,0000168
|
1324,2
|
1368,34
|
3
|
0,000023
|
0,0000219
|
0,22
|
-0,0000170
|
1368,34
|
1412,48
|
5
|
0,000037
|
0,0000354
|
0,17
|
-0,0000291
|
1412,48
|
1456,62
|
0
|
0
|
0,0000000
|
0,17
|
0
|
1456,62
|
1500,76
|
0
|
0
|
0,0000000
|
0,17
|
0
|
1500,76
|
1544,9
|
2
|
0,000013
|
0,0000129
|
0,15
|
-0,0000110
|
1544,9
|
1589,04
|
0
|
0
|
0,0000000
|
0,15
|
0,0000000
|
1589,04
|
1633,18
|
3
|
0,000019
|
0,0000184
|
0,12
|
-0,0000161
|
1633,18
|
1677,32
|
2
|
0,000012
|
0,0000119
|
0,1
|
-0,0000107
|
1677,32
|
1721,46
|
1
|
0,000006
|
0,0000058
|
0,09
|
-0,0000053
|
1721,46
|
1765,6
|
1
|
0,000006
|
0,0000057
|
0,08
|
-0,0000052
|
1765,6
|
1809,74
|
1
|
0,000006
|
0,0000055
|
0,07
|
-0,0000051
|
1809,74
|
1853,88
|
3
|
0,000017
|
0,0000162
|
0,04
|
-0,0000155
|
1853,88
|
1898,02
|
3
|
0,000016
|
0,0000158
|
0,01
|
-0,0000156
|
1898,02
|
1942,16
|
0
|
0
|
0,0000000
|
0,01
|
0
|
1942,16
|
1986,3
|
0
|
0
|
0,0000000
|
0,01
|
0
|
1986,3
|
2030,44
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2030,44
|
2074,58
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2074,58
|
2118,72
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2118,72
|
2162,86
|
0
|
0
|
0,0000000
|
0,01
|
0
|
2162,86
|
2207
|
1
|
0,000005
|
0,0000045
|
0
|
-0,0000045
|
Средняя наработка на отказ  = 900,48 (ч) = 900,48 (ч)
Графики:
Для n = 30:
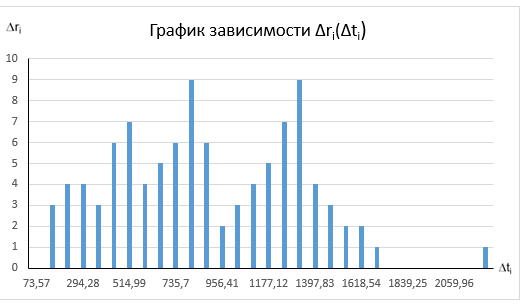



Для n = 40:
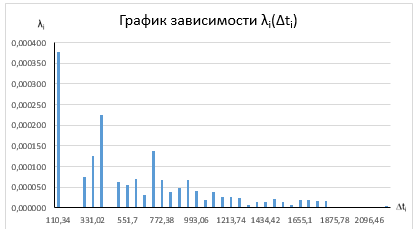
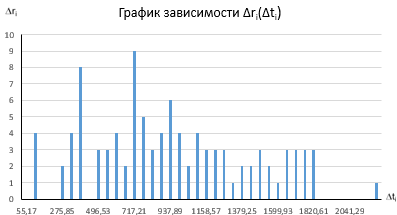


Для n = 50:




Выводы
Величина n не влияет на значения показателей надежности, это следует из графиков. Изменение величины n влияет на количество интервалов, на которое разбито максимальное время работы изделия. Это даёт больше контрольных точек исследования отказов, что помогает точнее составить график распределения во времени интенсивности и плотности отказов, а также графика надежности.
На основании полученных результатов по формулам были определены: 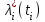 - интенсивность отказов, - интенсивность отказов,  - плотность распределения отказов (частота отказов), - плотность распределения отказов (частота отказов),  - вероятность безотказной работы и ∆ri(t) – кол-во отказов. По этим результатам были построены графики. - вероятность безотказной работы и ∆ri(t) – кол-во отказов. По этим результатам были построены графики.
По графику распределения отказов можно сделать вывод, что основная часть отказов наблюдается в середине периода испытаний.
По графику функции безотказной работы видно, что с течением времени вероятность безотказной работы уменьшается.
По графику интенсивности отказов видно, что с течение времени интенсивность отказов постепенно уменьшается достигая своего минимального значения.
По графику частоты отказов видно, что частота отказов уменьшается с течением времени.
|
 Скачать 168.97 Kb.
Скачать 168.97 Kb. ) вычисляется с помощью соотношения вида:
) вычисляется с помощью соотношения вида: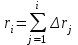 - число объектов, отказавших в интервале времени (0,
- число объектов, отказавших в интервале времени (0, ).
).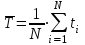
 , n=30; 40; 50
, n=30; 40; 50 = 900,48 (ч)
= 900,48 (ч) = 900,48 (ч)
= 900,48 (ч) = 900,48 (ч)
= 900,48 (ч)











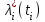 - интенсивность отказов,
- интенсивность отказов,  - плотность распределения отказов (частота отказов),
- плотность распределения отказов (частота отказов),  - вероятность безотказной работы и ∆ri(t) – кол-во отказов. По этим результатам были построены графики.
- вероятность безотказной работы и ∆ri(t) – кол-во отказов. По этим результатам были построены графики.
 ,
, 

 ,
,  ,
,  ,
,