Лабораторная работа тау. Цель работы освоение методов анализа линейных систем с помощью программы Vissim изучение основных характеристик типовых линейных звеньев. Задание к работе
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
Титульник Цель работы: освоение методов анализа линейных систем с помощью программы Vissim; изучение основных характеристик типовых линейных звеньев. Задание к работе: 1. Построить в Vissim’e переходные и весовые характеристики для трех заданных типовых динамических звеньев. 2. Проанализировать влияние изменения их параметров на переходные характеристики. 3. Записать уравнение передаточной функции, переходной и импульсной функций. Выполнение работы: 1. Апериодическое 2-го порядка(3): 1.1 Передаточная функция звена: 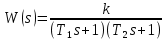 , где , где 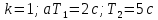 1.2 Переходная функция звена: 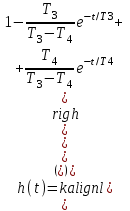 1.3 Импульсная функция звена: 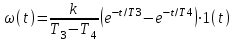 1.4 Получим графики переходных функций звена в Vissim 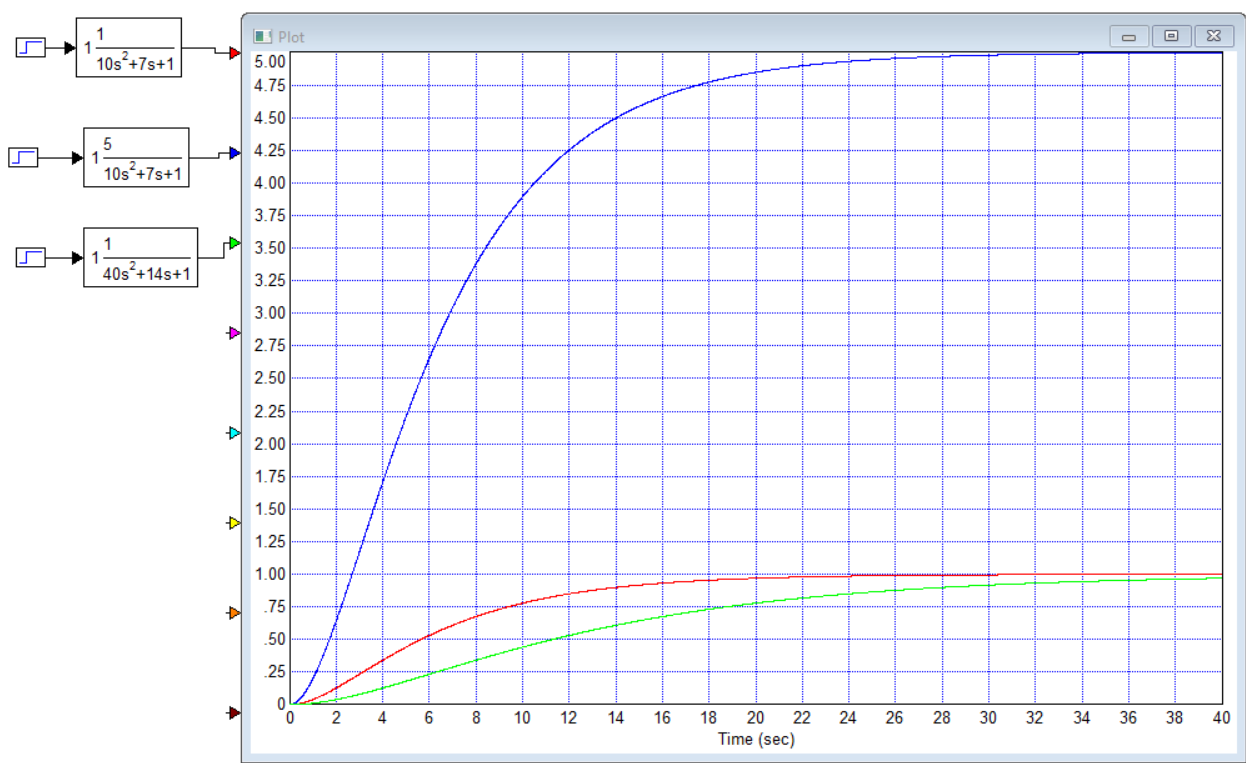 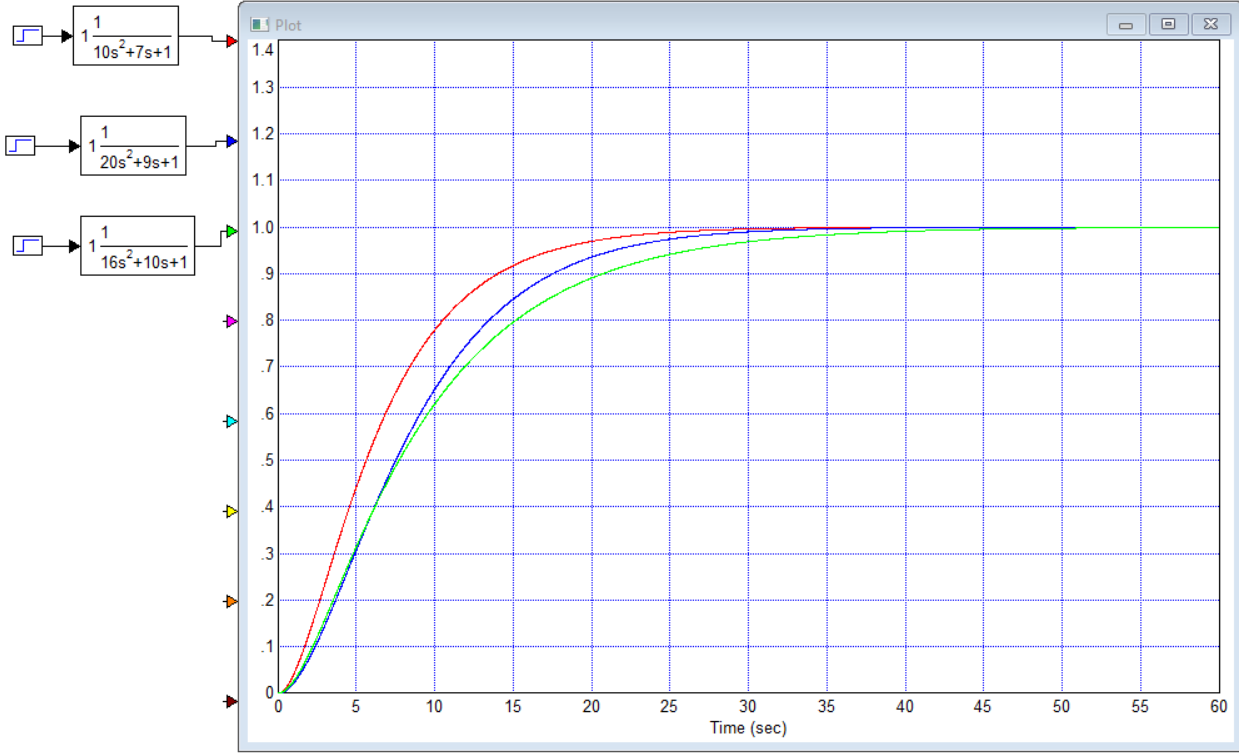 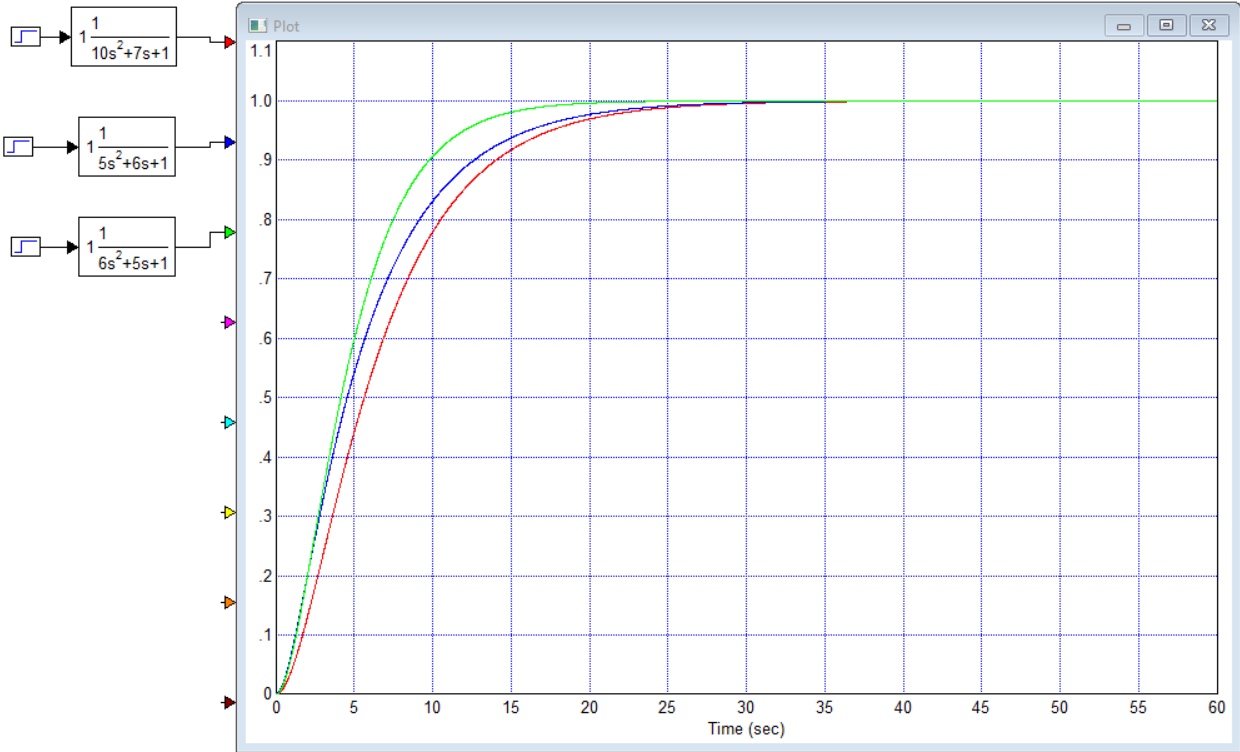 1.5 Получим графики импульсных функций звена в Vissim 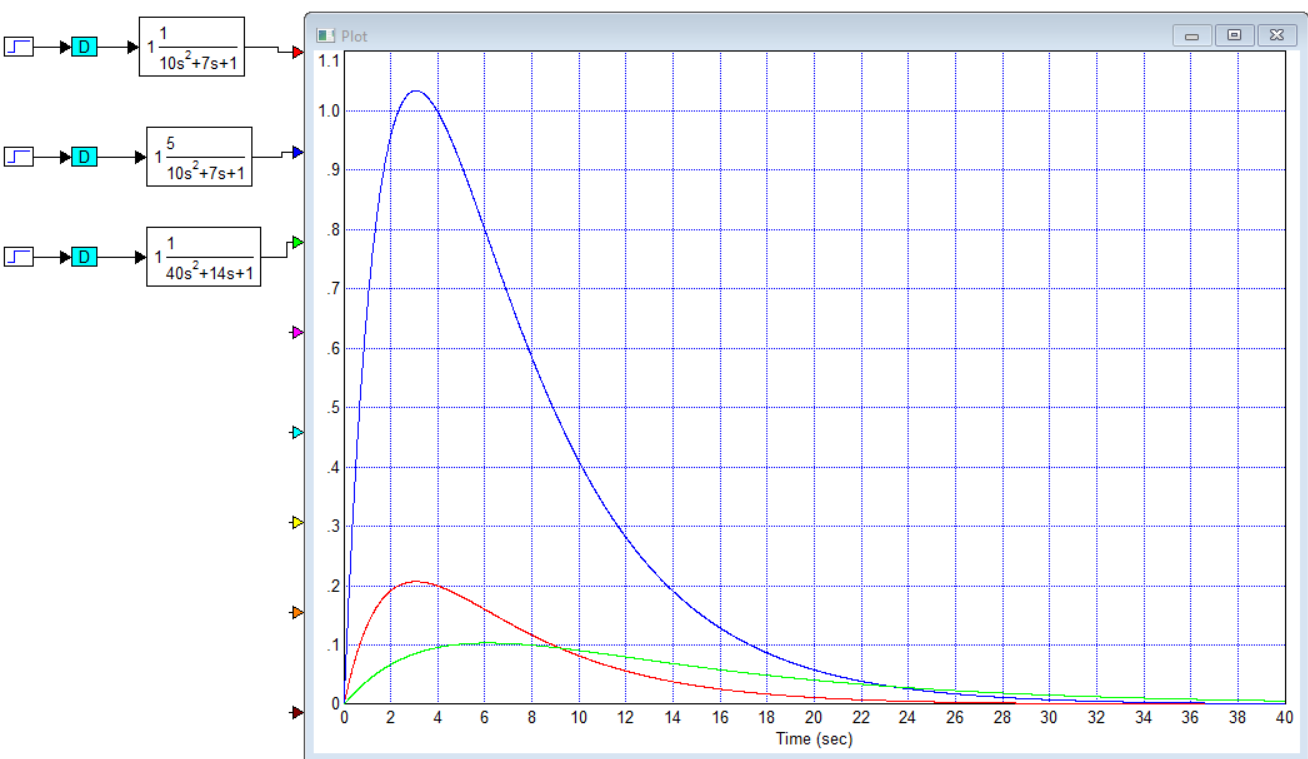 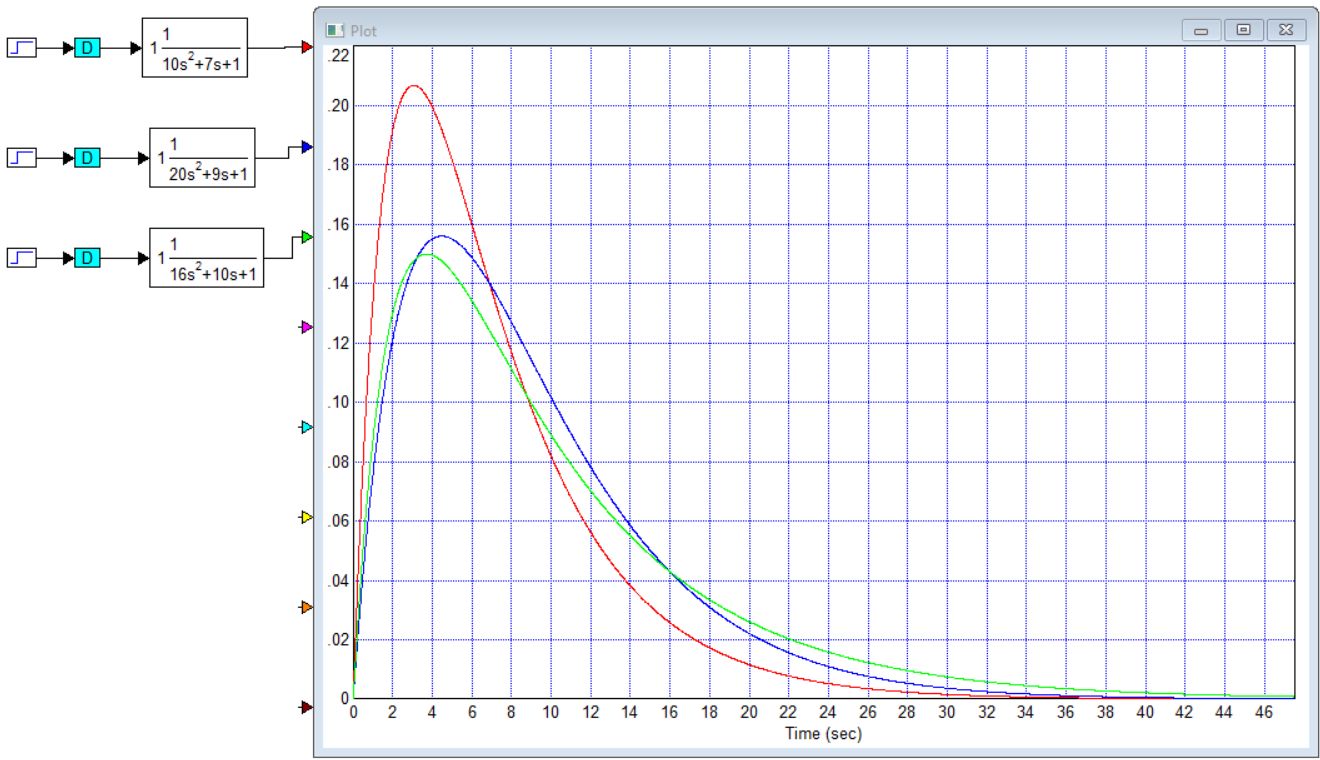 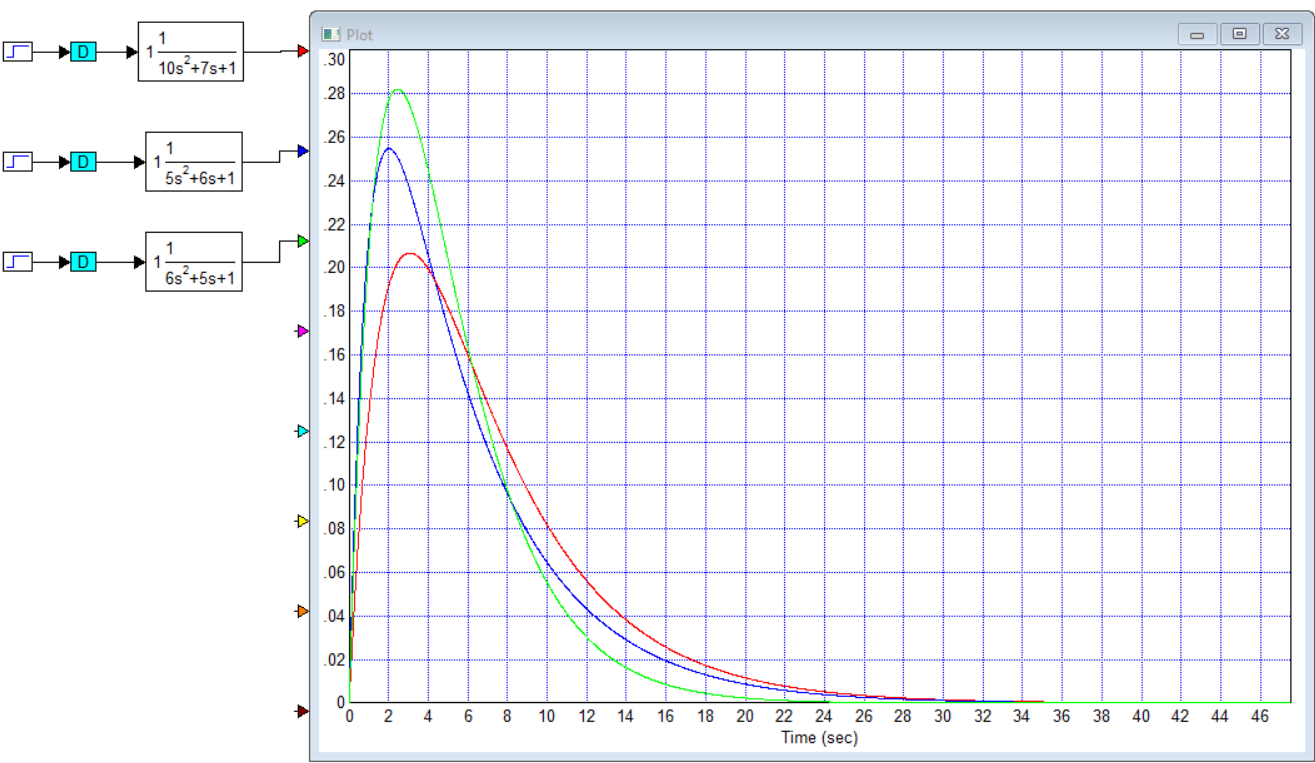 Вывод: при увеличении параметра k = 5, на графике переходной функции увеличивается амплитуда сигнала, на графике весовой функции аналогично. При увеличении коэффициентов 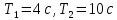 , на графике переходной функции увеличивается время сигнала с уменьшением амплитуды, на графике весовой функции аналогично. , на графике переходной функции увеличивается время сигнала с уменьшением амплитуды, на графике весовой функции аналогично.При увеличении только коэффициента 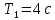 , на графике переходной функции уменьшается амплитуда, на графике весовой функции аналогично, с увеличением времени сигнала. , на графике переходной функции уменьшается амплитуда, на графике весовой функции аналогично, с увеличением времени сигнала. При увеличении только коэффициента 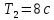 , на графике переходной функции уменьшается амплитуда с увеличением времени сигнала, на графике весовой функции аналогично. , на графике переходной функции уменьшается амплитуда с увеличением времени сигнала, на графике весовой функции аналогично. При уменьшении только коэффициента 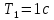 , на графике переходной функции увеличивается амплитуда, на графике весовой функции аналогично. , на графике переходной функции увеличивается амплитуда, на графике весовой функции аналогично. При уменьшении только коэффициента 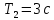 , на графике переходной функции увеличивается амплитуда с уменьшением времени сигнала, на графике весовой функции аналогично. , на графике переходной функции увеличивается амплитуда с уменьшением времени сигнала, на графике весовой функции аналогично. 2. Колебательное(4): 2.1 Передаточная функция звена: 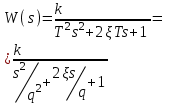 , где , где 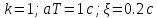 2.2 Переходная функция звена: 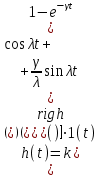 2.3 Импульсная функция звена: 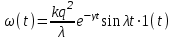 2 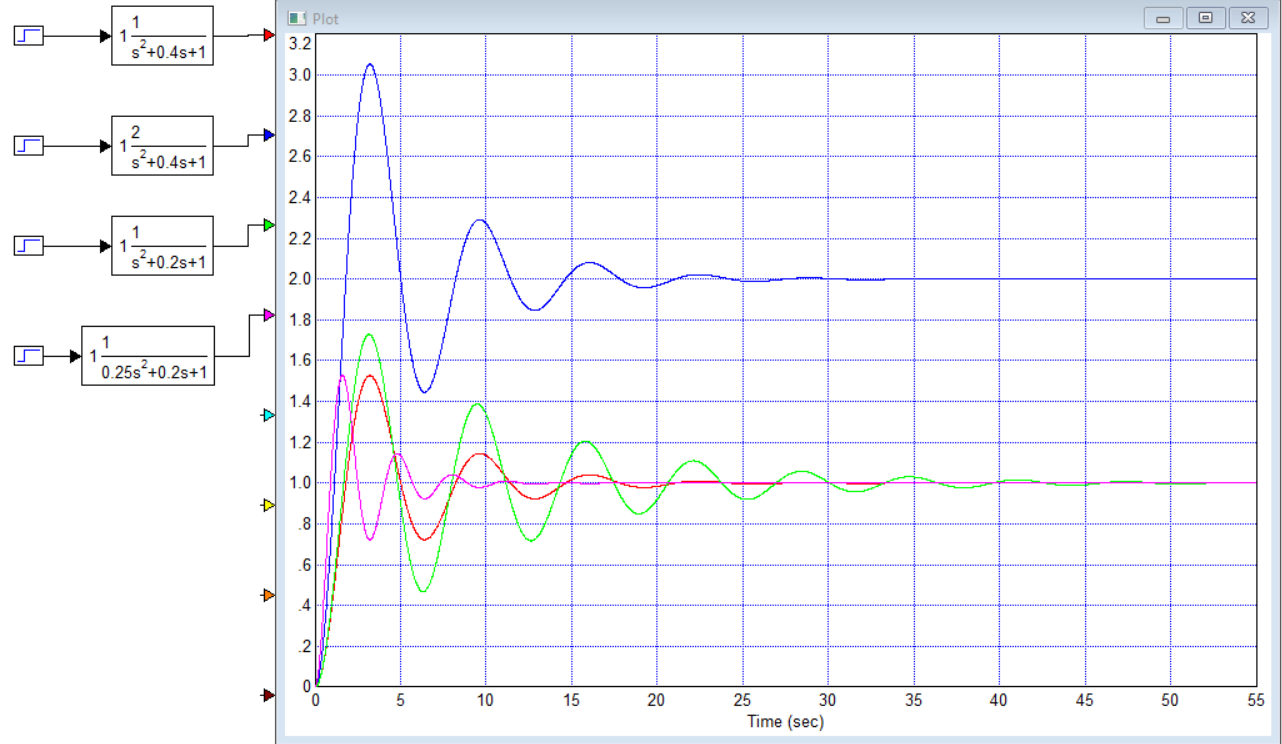 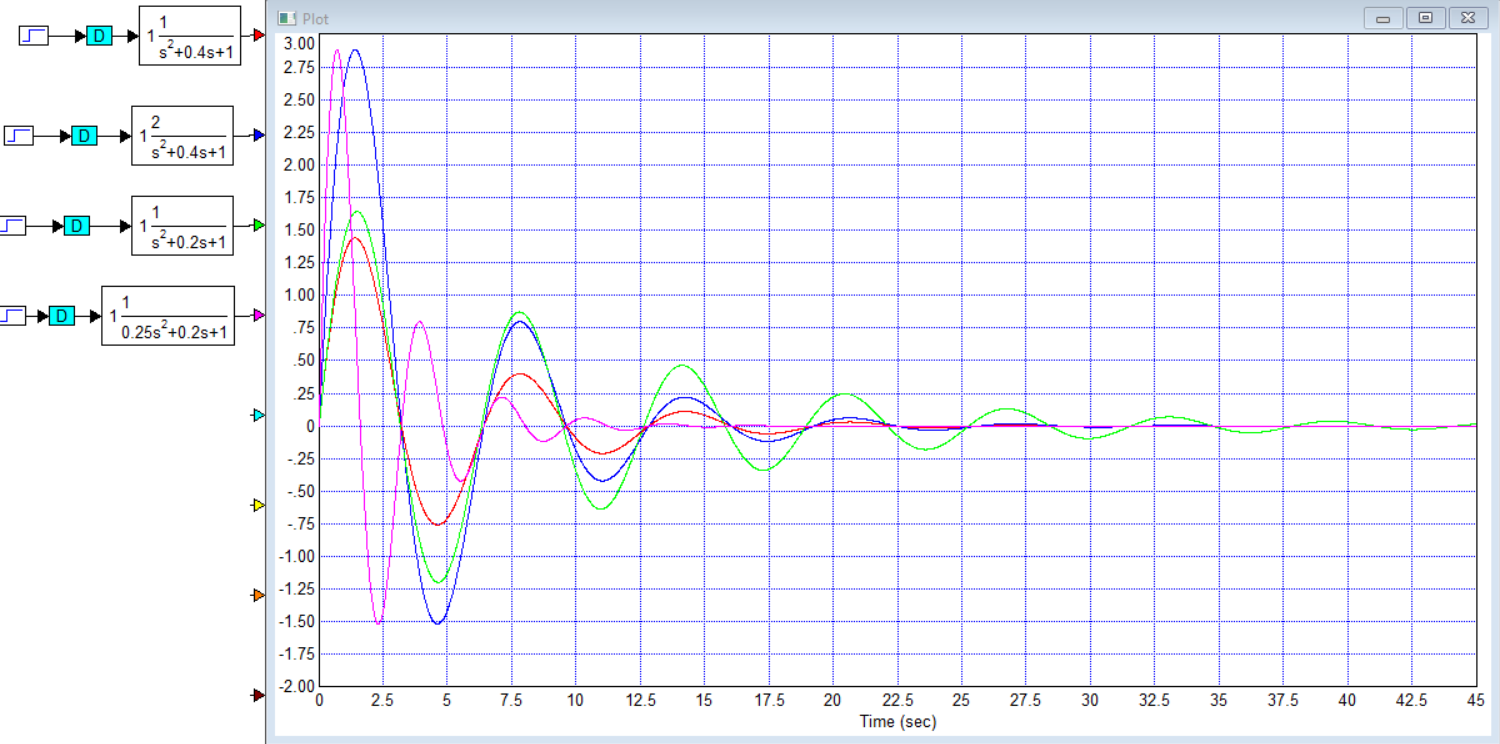 .4 Получим графики переходной и импульсной функций звена в Vissim Вывод: 1) При увеличении значения 𝑘 можно наблюдать изменение амплитуды. 2) При уменьшении значения ξ (в 2 раза) мы можем наблюдать увеличение амплитуды и времени переходного процесса. 3) При уменьшении 𝑇 можно наблюдать уменьшение времени переходного процесса и увеличение амплитуды. 2. Идеальное интегрирующее(6): 2.1 Передаточная функция звена: 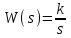 , где , где 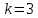 2.2 Переходная функция звена: 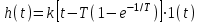 2.3 Импульсная функция звена: 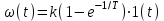 2.4 Получим графики переходной и импульсной функций звена в Vissim 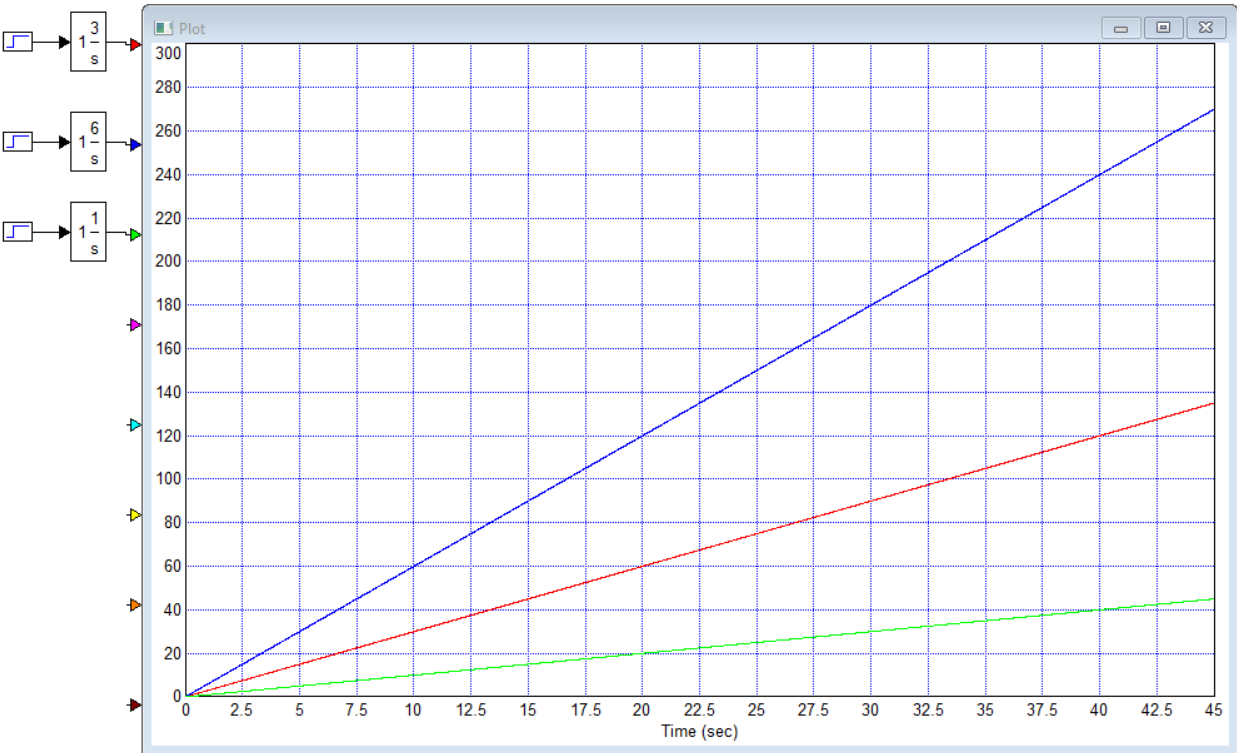 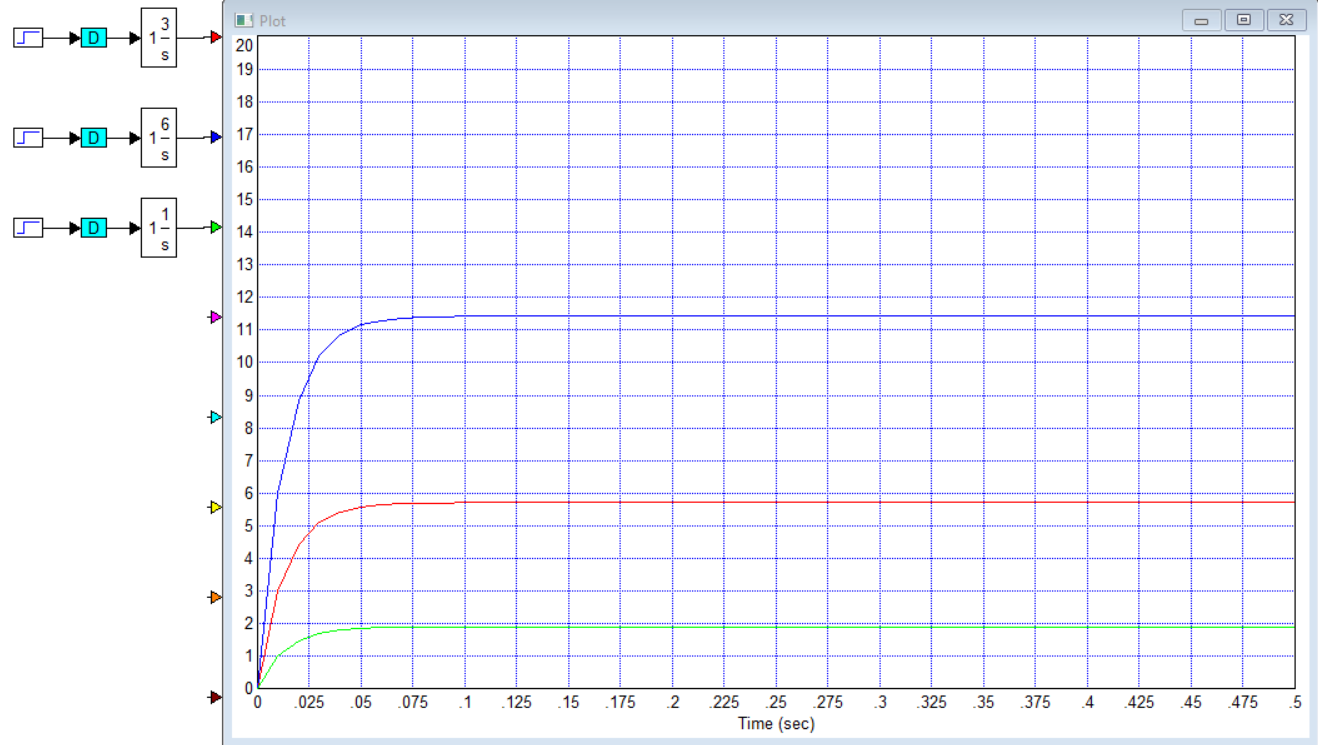 Вывод: При изменении параметра k изменяется только амплитуда. Она возрастает при увеличении параметра и уменьшается при его уменьшении. Ответы на контрольные вопросы: 1) Передаточная функция W(s) – отношение изображения выходного сигнала Y(s) к изображению входного сигнала X(s) 2) Переходная характеристика h(t) – реакция звена на ступенчатое единичное воздействие 1(t) 3) Импульсная (или весовая) функция w(t) – реакция звена на дельта-функцию Дирака d(t) 4) В зависимости от выбранного звена может измениться амплитуда, время сигнала, частота сигнала и т.п. 5) Типовые звенья: простейшие (пропорциональное звено, интегратор и диффе-ренцирующее звено); звенья первого порядка (апериодическое или инерционное, инерционно-дифференцирующее, форсирующее и др.); звено второго порядка (колебательное и его частный случай – апериодическое второго порядка); звено третьего порядка (способное терять устойчивость, его можно назвать звеном Вышнеградского); звено запаздывания. Основные характеристики линейных звеньев: А) передаточная функция W(s) – отношение изображения вы-ходного сигнала Y(s) к изображению входного сигнала X(s); Б) переходная характеристика h(t) – реакция звена на ступен-чатое единичное воздействие 1(t); В) импульсная (или весовая) функция w(t) – реакция звена на дельта-функцию Дирака d(t); Г) комплексный коэффициент передачи (частотная переда-точная функция) W(jw) – это отношение спектра вы-ходного сигнала Y(jw) к спектру входного X(jw). 6) Характеристическое уравнение представляет собой знаменатель передаточной функции, приравненный к нулю. Корни характеристического уравнения могут быть вещественными, комплексно-сопряженными и комплексными, что определяется параметрами системы. |
