Исследование генератора линейно–изменяющегося напряжения». ВТиИТ лабораторная №2. Цель работы

• Название: Цель работы
• Анкор: Исследование генератора линейно–изменяющегося напряжения
• Дата: 16.12.2020
• Размер: 207.2 Kb.
• Имя файла: ВТиИТ лабораторная №2.docx
• Тип: Исследование; #161343

Цель работы:

Изучение ГЛИН; исследование влияния номиналов компонентов схемы на форму выходного сигнала ГЛИН; измерение качественных показателей ГЛИН.

Описание схемы:

Схема ГЛИН в формате EWВ показана на рис. 2.1.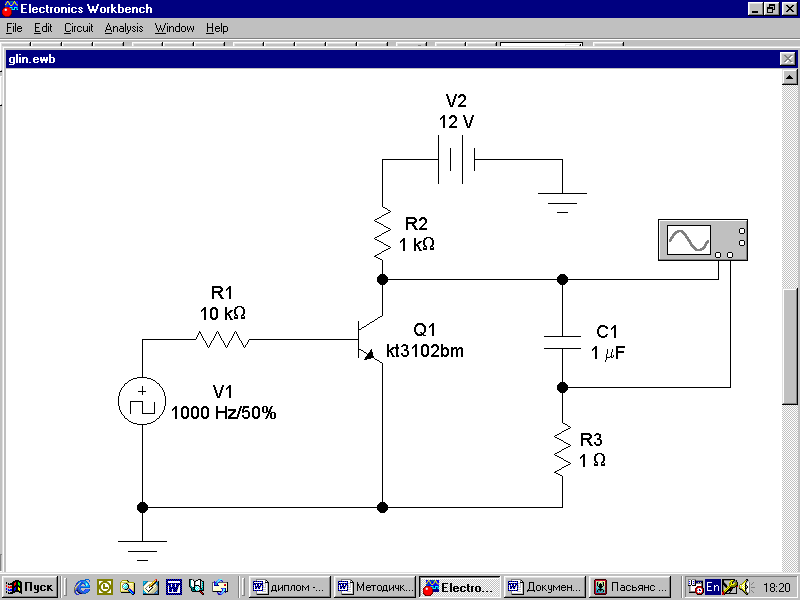



Схема представляет из себя простейший генератор линейно–изменяющегося напряжения на биполярном транзисторе Q1 (КТ3102). Резистор R2 и конденсатор С1 образуют формирующую цепь ГЛИН. Резистор R3 номиналом 1 Ом предназначен для измерения тока в цепи конденсатора С1, т.к. программа EWB не позволяет выводить осциллограммы тока в ветвях схемы.

Ход работы:

Установим следующие варианты номиналов компонентов схемы:

1. 
   R2 = 100 Ом; С1 = 1 мкФ.
   
2. 
   R2 = 10 кОм; С1 = 1 мкФ;
   
3. 
   3) R2 = 10 Ом; С1 = 10 мкФ.
   

1.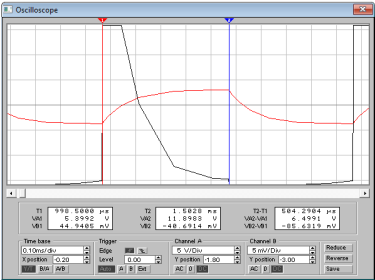





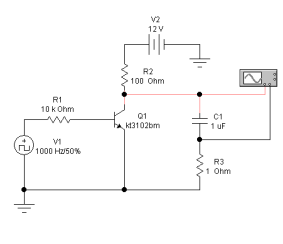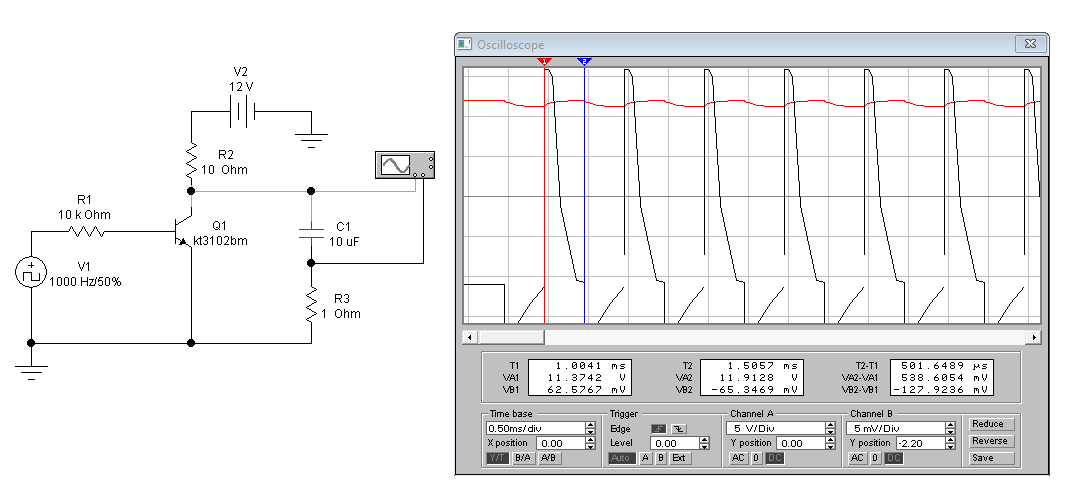=63.9089/12=5.3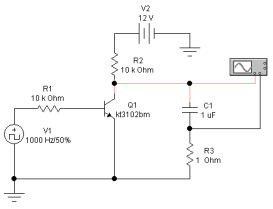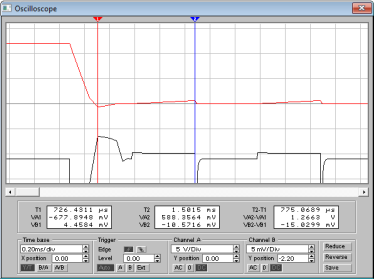2574

=(5.3992-11.8998)/5.3992= −1,20399

2.





=62,57/12 = 5,2

=(11,37-11,91)/11,37 = -0,047

3.





=4.4584/12=0,371533

=(-677.8948-588.3564)/(-677.8948)= 1,86792

Контрольные вопросы:

1. Схема простейшего ГЛИН состоит из времязадающего конденсатора С, резистора Rк и транзисторного ключа VT1. На вход транзисторного ключа подается последовательность прямоугольных импульсов с заданным интервалом между

импульсами и длительностью. Когда на базе транзистора нулевое напряжение (промежуток времени между импульсами), транзистор закрыт и происходит заряд конденсатора через резистор Rк.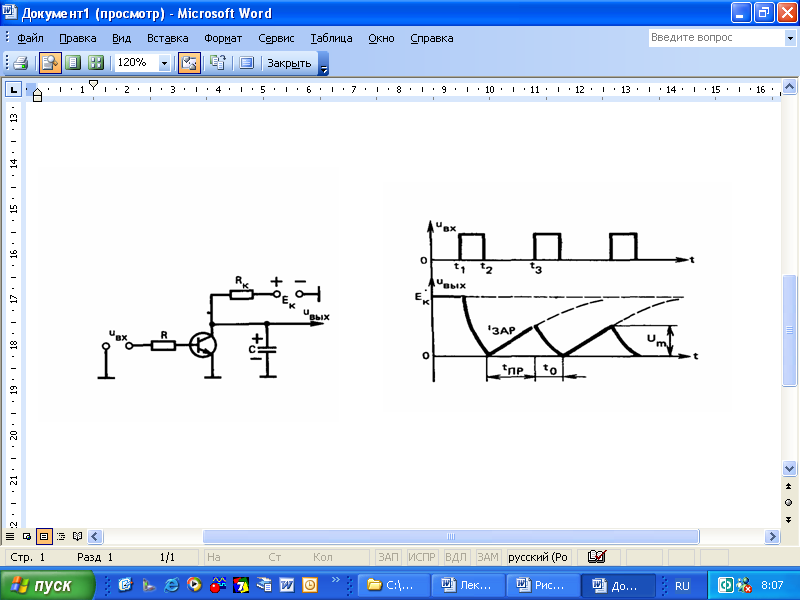



2. Известно, что линейная функция характеризуется постоянст­вом производной во всех ее точках. Поэтому отклонение от линей­ного закона можно оценивать коэффициентом нелинейности, оп­ределяемым как относительное изменение производной функ­ции, т. е.

α = [ (du_ВЫХ./dt)_НАЧ - (du_ВЫХ./dt)_КОН] / (du_ВЫХ./dt)_НАЧ .

В простейшем ГЛИН U_вых = Uс и это соотношение принима­ет вид:

α = [ (du_С./dt)_НАЧ - (duС_./dt)_КОН] / (du_С./dt)_НАЧ

где (du_С./dt)_НАЧи (duС_./dt)_КОН — скорость изменения напряжения на конденсаторе в начале и конце прямого хода.

Параметр α характеризует степень отклонения кривой напря­жения на конденсаторе от линейно-изменяющегося закона. Этот параметр может быть определен также через ток, протекающий через конденсатор в процессе заряда.

Последней характеристикой линейно-изменяющегося напряже­ния является коэффициент использования напряжения источни­ка питания β, который показывает, насколько амплитуда пилооб­разного напряжения меньше амплитуды, до которой мог бы за­рядиться конденсатор:

β = Uм / Ек .

Сравнивая последние формулы для схемы простого генератора, мо­жно сделать вывод о том, что для нее α = β , т. е. коэффициент не­линейности равен коэффициенту использования.

3. Сравнивая формулы для схемы простого генератора, можно сделать вывод о том, что для нее α = β , т. е. коэффициент не-линейности равен коэффициенту использования. Это существенный недостаток простой схемы ГЛИН, поскольку уменьшение α приводит и к уменьшению β. Если, например, требуется обеспечить коэффициент нелинейности α = 1%, то амплитуда выходного напряжения будет составлять только 0,01Ек.

4. С изменением постоянной времени форма выходного напряжения будет выглядеть более линейной, при большей постоянной времени. С ростом постоянной времени график выходного напряжения всё больше и больше будет похож на линейный, а не на кривую. Это выражается следующим законом: α ≈ tnp / τ.

Вывод: мы изучили ГЛИН; исследование влияния номиналов компонентов схемы на форму выходного сигнала ГЛИН; измерение качественных показателей ГЛИН.