физика лабораторная работа. отчет по лабораторной работе №1 - копия. Цели работы. Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.

• Название: Цели работы. Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.
• Анкор: физика лабораторная работа
• Дата: 06.11.2020
• Размер: 172.5 Kb.
• Имя файла: отчет по лабораторной работе №1 - копия.doc
• Тип: Закон; #148371

Цели работы.

• 
  Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.
  
• 
  Экспериментальное подтверждение закономерностей эффекта Комптона.
  
• 
  Экспериментальное определение комптоновской длины волны электрона.
  

Приборы и принадлежности:

- набор рентгеновских трубок с анодами из различных металлов;

- набор металлических монокристаллических образцов.

Краткая теория.
Модели электромагнитного излучения (ЭМИ):

• 
  луч - линия распространения ЭМИ (геометрическая оптика);
  
• 
  волна - гармоническая волна, имеющая амплитуду и определенную длину волны λ и частоту ν (волновая оптика);
  
• 
  кванты - фотоны, имеющие энергию, определяющуюся частотой излучения (согласно гипотезе Планка), распространяющиеся со скоростью с=3·10⁸ м/с (квантовая оптика).
  

Характеристики всех моделей связаны друг с другом.

Эффект Комптона заключается в появлении рассеянного излучения с большей длиной волны, зависящей от угла рассеяния, при облучении вещества монохроматическим рентгеновским излучением.

Рентгеновским называется электромагнитное излучение, которое можно моделировать с помощью электромагнитной волны с длиной от 10^-12 до 10^-8 м (частотой от 10¹⁶ до 10²⁰ с^-1), или с помощью потока фотонов с энергией от 100 эВ до 10⁶ эВ.

Согласно гипотезе Планка энергия ЭМИ W может испускаться и поглощаться веществом квантами (порциями):
или (1),
где: W – энергия кванта (фотона),

ν – частота излучения,

ω = 2πν – циклическая частота,

h – постоянная Планка: h = 6,625·10⁻³⁴ Дж·с,

ћ = h/2π = 1,054·10⁻³⁴ Дж·с.
Как и любая движущаяся частица, фотон характеризуется импульсом p:
(2),
где: m – масса фотона,

с = 3·10⁸ м/с – скорость фотонов.
С учетом известной формулы Эйнштейна:
(3)
выводится формула для вычисления импульса фотона:
(4),
где: k = 2π/λ – волновое число.
Схема проведения эксперимента для исследования эффекта Комптона представлена на рис. 1.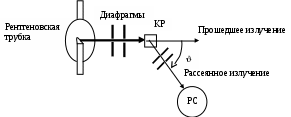


Рис. 1. Схема опыта по изучению рассеяния рентгеновского излучения монокристаллом.
Рисунок установки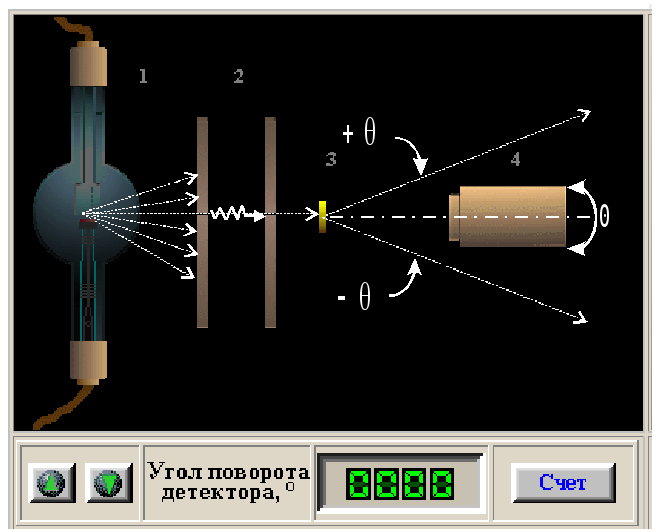



Излучение с длиной волны λ, испускаемое рентгеновской трубкой после взаимодействия с металлическим монокристаллом КР рассеивается, и наряду с излучением с исходной длиной волны λ рентгеновский спектрометр РС регистрирует рассеянное излучение с длиной волны λ’ ˃ λ, зависящей от угла рассеяния .

 = ’ -  = _C (1 - cos) (5),
где _C = - константа, комптоновская длина волны,

m – масса покоя рассеивающей частицы.
Для электрона _C = 2,43 10^-12 м.

Исходная длина волны  рентгеновского излучения зависит от металла, из которого изготовлен анод рентгеновской трубки.

Объяснение эффекта Комптона базируется на использовании квантовой модели ЭМИ.

Рассмотрим процесс столкновения падающего рентгеновского фотона (энергия , импульс ) с почти покоящимся свободным электроном металлического вещества. Энергия электрона до столкновения равна его энергии покоя mc², где m – масса покоя электрона. Импульс электрона практически равен нулю.

После столкновения электрон будет обладать импульсом и энергией, равной . Энергия фотона станет равной ’ , а импульс ’.

Из законов сохранения энергии и импульса вытекают два равенства:

 + mc² = ’ + (6)

= + ’.

Разделив первое равенство на второе, возведя в квадрат и проведя некоторые преобразования, получим формулу Комптона (5).

Задание № 1 – определение зависимости разности длин волн ∆λ прошедшего и рассеянного излучений (комптоновского сдвига) от угла рассеяния.

Монокристалл – железо

Трубка с анодом - железо

№ изм.	Угол ϑ,ͦ	Сдвиг ∆λ, 10-12 м
1	0	191
2	3	192
3	6	193
4	9	194
5	12	195
6	15	196
7	18	197
8	21	198
9	24	199
10	27	200
11	30	201
12	33	202
13	36	203
14	39	204
15	42	205
16	45	206
17	48	207
18	51	208
19	54	209
20	57	210
21	60	211
22	63	212
23	66	213
24	69	214
25	72	215
26	75	216
27	78	218
28	81	220
29	84	222
30	87	224

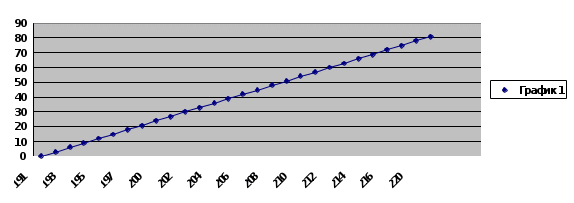Задание № 2 – определение зависимости комптоновского сдвига от угла рассеяния при использовании рентгеновских трубок.

№ изм.	λFe		λNi		λAg
	ϑ,ͦ	∆λ, 10-12 м	ϑ,ͦ	∆λ, 10-12 м	ϑ,ͦ	∆λ, 10-12 м
1	15	201	15	198	15	190
2	3	188	3	188	3	188
3	9	190	9	190	9	189

Вывод: С увеличением угла интенсивность смещенной компонент растет, а несмещенной - падает.
Задание № 3 – определение зависимости комптоновского сдвига от угла рассеяния при использовании разных кристаллов.

№ изм.	Fe		Ni		Ag
	ϑ,ͦ	∆λ, 10-12 м	ϑ,ͦ	∆λ, 10-12 м	ϑ,ͦ	∆λ, 10-12 м
1	15	196	15	165	15	58
2	3	193	3	160	3	55
3	9	195	9	163	9	56

Вывод: Наблюдаемое комптоновское смещение не зависит от материала рассеивающего образца и длины волны падающего излучения, а определяется лишь углом между направлениями рассеянного и падающего излучений.