Биология. реферат по геометрии. Центральная и осевая симметрия
 Скачать 86.63 Kb. Скачать 86.63 Kb.
|
|
Муниципальное бюджетное общеобразовательное Учреждение средняя общеобразовательная школа №55 Реферат По геометрии На тему: «Центральная и осевая симметрия» Выполнила: Ученица 8-А класса Менькова Д.А. Проверила: Кондратьева С.В. Ижевск 2018 Содержание: Введение…………………………………………………………………… Глава 1. Симметрия(теория) Глава 2. Центральная симметрия……………………………………….. Глава 3. Осевая симметрия………………………………………………. Глава 4. Последовательность построения………………………………... Глава 5. Примеры построения…………………………………………….. Список литературы………………………………………………….……. Симметрия Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг повёрнутый вокруг своего центра будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию). Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования. Симметрия: 1.Осевая 2.Центральная 3.Вращательная 4.Симметрия относительно точки 5.Скользящая симметрия В этом реферате я вам расскажу про центральную и осевую симметрию Центральная симметрия Центральная симметрия--Симметрия относительно точки или центральная симметрия - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам. Понятие «центральная симметрия» фигуры предполагает существование определенной точки – центра симметрии. По обе стороны от него располагаются точки, принадлежащие этой фигуре. Каждая из них имеет симметричную себе. Следует сказать, что понятие о центре отсутствует в Евклидовой геометрии. При этом в одиннадцатой книге, в тридцать восьмом предложении, есть определение пространственной симметричной оси. Понятие центра впервые появилось в 16-м веке. Центральная симметрия присутствует в таких известных всем фигурах, как параллелограмм и окружность. И у первой, и у второй фигуры центр один. Центр симметрии параллелограмма расположен в точке пересечения прямых, вышедших из противоположных точек; в окружности – это центр ее самой. Для прямой характерно наличие бесконечного количества таких участков. Каждая ее точка может являться центром симметрии. У прямого параллелепипеда существует девять плоскостей. Из всех симметричных плоскостей три перпендикулярны ребрам. Другие шесть проходят сквозь диагонали граней. Однако существует фигура, которая его не имеет. Ею является произвольный треугольник. Осевая симметрия Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией. Осевая симметрия — это симметрия относительно проведённой прямой (оси). Последовательность построения центральной симметрии. Точки M и M1 симметричны относительно некоторой точки O, если точка O является серединой отрезка MM1. 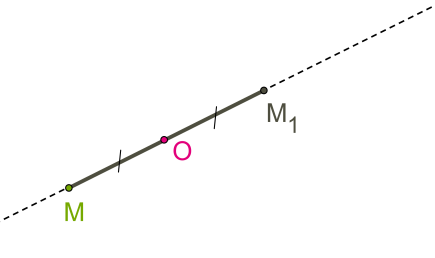 Точка O называется центром симметрии. 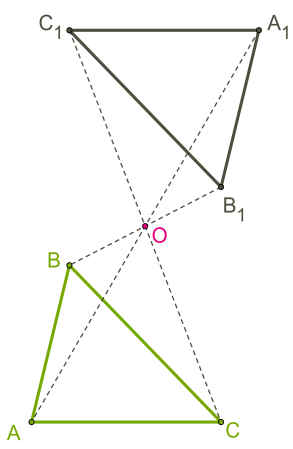 Построим треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки) O: 1. Для этого соединим точки A, B, C с центром O и продолжим эти отрезки; 2. Измерим отрезки AO, BO, COи отложим с другой стороны от точки O, равные им отрезки AO=OA1;BO=OB1;CO=OC1; 3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC. Последовательность Построения осевой симметрии Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии. 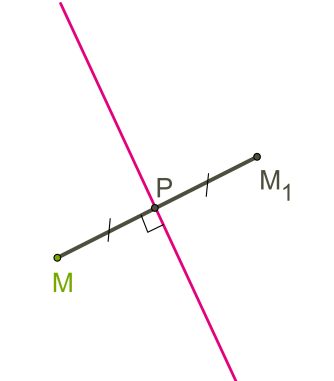 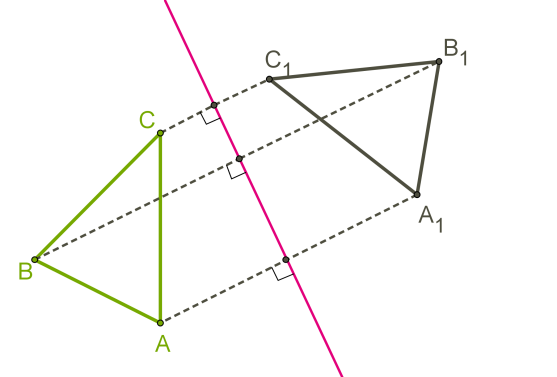 Построим треугольник A1B1C1, симметричный треугольнику ABC относительно красной прямой: 1. Для этого проведём из вершин треугольника ABC прямые, перпендикулярные оси симметрии и продолжим их дальше на другой стороне оси. 2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния. 3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC. Список литературы Справочник по элементарной математике. М.Я. Выгодский. – Издательство « Наука». – Москва 1971г. – 416стр. Справочник по математике для средних учебных заведений. А.Г. Цыпкин. Под редакцией С.А. Степанова. – Издательство «Наука». – Москва 1984г. – 480 стр. История математики в школе IX - X классы. Г.И. Глейзер. – Издательство «Просвещение». – Москва 1983г. – 351стр. Эстетика урока математики. И.Г. Зенкевич. – Издательство «Просвещение». – Москва 1981г. – 79 стр. Наглядная геометрия 5 – 6 классы. И.Ф. Шарыгин, Л.Н. Ерганжиева. – Издательство «Дрофа», Москва 2005г. – 189стр. Ресурсы сети Интернет. https://ru.wikipedia.org/wiki/Симметрия. https://www.yaklass.ru/p/matematika/6-klass/geometricheskie-figury-i-tela-simmetriia-na-ploskosti-13781/osevaia-i-tcentralnaia-simmetriia-14716/re-e5fbbd9b-0519-4f8d-88ee-4bdcfa44b87b. |
