четырехполюсник сверхвысокий частота прибор. Четырехполюсник сверхвысокий частота прибор
 Скачать 235.35 Kb.
|
|
четырехполюсник сверхвысокий частота прибор Диапазон СВЧ становится все более популярным в связи с бурным развитием разных областей науки и техники, таких как связь с космическими объектами и радиолокация, радиоуправление, связь, телевидение, промышленная электроника. Вследствие чего требования к параметрам устройств, работающим в диапазоне СВЧ, увеличиваются и, следовательно, возникает необходимость создания специальных средств измерения, проверки и настройки устройств СВЧ. Для решения этой задачи используют измерители комплексных коэффициентов передачи и отражения (модуля и фазы) четырехполюсников СВЧ или измерители S - параметров. В настоящий момент в мире существует аппаратура, позволяющая измерять комплексные коэффициенты передачи и отражения в диапазоне частот до 110 ГГц и амплитудном диапазоне до 136 дБ. Для разработчиков измерителей комплексных коэффициентов передачи и отражения СВЧ устройств основной целью является увеличение частотного и амплитудного диапазона измеряемых величин. Настоящая курсовая работа посвящена рассмотрению методов измерения комплексных характеристик четырехполюсников СВЧ. Цель этой работы - изучить методы измерения комплексных характеристик четырехполюсников СВЧ. При этом существенным является решение следующих задач: - изучить и проанализировать все существующие методы измерения комплексных характеристик четырехполюсников СВЧ ; - провести сравнение всех известных методов; - изучить приборы, использующиеся для измерения комплексных характеристик четырехполюсников СВЧ. Элементы теории четырехполюсников и матриц В [1] дается определение четырехполюснику как электрическому устройству, имеющему две пары зажимов (полюсов), одна из которых служит для подключения системы к источнику энергии (генератору), а другая - к потребителю энергии (нагрузке). Зажимы, к которым присоединен генератор, называют входными, а зажимы, к которым присоединена нагрузка, - выходными зажимами четырехполюсника. Известно, что каждый четырехполюсник может быть описан одной из систем параметров [a], [z], [y], [h], которые не несут информации о характерных особенностях диапазона СВЧ, его коэффициентах отражения, связанных с электрическими неоднородностями СВЧ тракта. Для СВЧ диапазона дополнительно разработаны две системы [s] и [t] параметров, устраняющие отмеченные недостатки. В диапазоне СВЧ каждый четырехполюсник характеризуется падающими Uпад и отраженными Uотр волнами напряжений. Рассмотрим особенности систем параметров характеризующих четырехполюсник в диапазоне СВЧ. Начнем с рассмотрения системы [s] параметров. 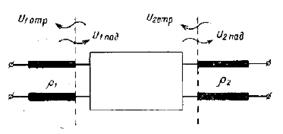 Рисунок 1 - Четырехполюсник в СВЧ диапазоне На рисунке 1 приведен четырехполюсник в СВЧ диапазоне, который описывается следующей системой уравнений:  (1) Такая система уравнения называется матрицей рассеяния, т.к. в левой ее части находится волны напряжения, отходящие и рассеиваемые от четырехполюсника. Но матрица рассеяния это индивидуальная матрица, описывающая конкретный четырехполюсник и, к сожалению, по своему построению она не пригодна для расчета общих параметров каскадно соединенных СВЧ четырехполюсников, правые ее части принадлежат разным входам. Поэтому для расчетов каскадно соединенных СВЧ четырехполюсников применяют t-параметры, представляющие собой элементы матрицы передачи, которая имеет следующий вид: 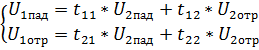 (2) Представим элементы матрицы рассеяния в следующем виде. Применяя режимы КЗ и ХХ и СН к (1) имеем:  При (КЗ) имеем: - коэффициент передачи четырехполюсника в обратном направлении  ; - коэффициент отражения выхода  ;  При (ХХ) имеем: - коэффициент отражения входа  ; - коэффициент передачи от входа к выходу  . В [2] указывается, что матрицы рассеяния удобно применять при решении задач по согласованию устройств СВЧ, расчету погрешностей, обуславливаемых отражениями, и т.д. С другой стороны, в ряде случаев, например, при исследовании каскадного соединения нескольких устройств СВЧ применение матриц рассеяния становится затруднительным. В этом случае пользуются матрицами передачи. Матрица рассеяния [s] параметров и матрица передачи [t] параметров являются ненормативными матрицами. Отметим, что к ненормативным матрицам также относятся матрицы параметров, не применяемых в диапазоне СВЧ, такие как: - матрица передачи  - матрица сопротивлений - матрица проводимостей    Рисунок 2 - Направление токов и напряжений в четырехполюснике при прямой передаче Для четырехполюсника, представленного на рисунке 2, можно записать:  (3)  (4)  (5) где ,, - напряжения и токи на входе и выходе четырехполюсника (рисунок 2). Величины выражений (1) - (5) связаны следующими соотношениями: 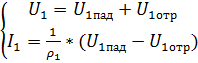 (6) 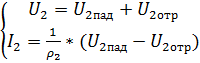 (7)  Выполняя в уравнениях (1) - (5) тождественные преобразования, можно заменить напряжения и токи нормированными напряжениями и токами, имеющими размерность (или корня из мощности); все элементы матриц становятся при этом безразмерными. Нормированные матрицы обозначаются прописными буквами алфавита, ненормированные - строчными. 3.5.Свойства многополюсников и их матриц [s]Нормированные матрицы  обладают двумя замечательными свойствами, связанными с физическими свойствами многополюсников.Свойство 1. Взаимному многополюснику соответствует симметричная нормированная матрица рассеяния  .Из общей теории электрических цепей известно, что для взаимного многополюсника должно выполняться соотношение Yk i = Yi k, (3.25) т.е. матрица проводимости взаимного многополюсника симметрична относительно главной диагонали. Аналогичным свойством будет обладать согласно (3.22) и нормированная матрица  . Из соотношений ( 3.23 ) между и следует, что в этом случае (3.26)Т.е. нормированная матрица также симметрична относительно главной диагонали. Соотношение (3.26) означает, что внутри многополюсника передача энергии междуi- ым и k -ым входами не зависит от направления передачи энергии. Взаимность многополюсника определяется по отсутствию внутри его невзаимных элементов: диодов, транзисторов, намагниченных ферритов и плазмы и обычно легко определяется самим типом многополюсника.Свойство 2. Недиссипативному многополюснику соответствует унитарная нормированная матрица рассеяния .Недиссипативным (реактивным) многополюсником называется многополюсник, внутри которого отсутствуют потери энергии. Конечно, реально внутренние потери всегда присутствуют, но они могут быть пренебрежимо малы по сравнению с общей мощностью на входах многополюсника. Очевидно, что для недиссипативного многополюсника закон сохранения энергии может быть записан так  , (3.27)т.е. суммы мощностей всех падающих и отраженных волн должны быть равны. Обозначим 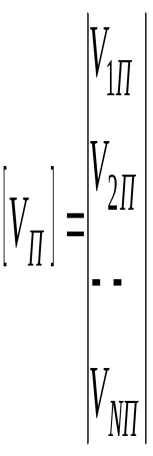 вектор-столбец нормированных напряжений падающих волн и  - вектор- строка этих же напряжений (знак “Т” означает транспонирование матрицы). Тогда, согласно правилу перемножения матриц, , (3.28)где знак “*” означает комплексно – сопряженную матрицу. Аналогично для отраженных волн, сумма их мощностей во всех плечах может быть записана в виде  . (3.29)Подставим в (3.27) соотношение  и учтем, что при транспонировании произведения матриц меняется их порядок в произведении . (3.30)Приравнивая (3.28) и (3.30) приходим к соотношению   . (3.31)Из него следует, что для недиссипативных (реактивных) многополюсников и их нормированных матриц рассеяния должно быть справедливо следующее утверждение: Произведение транспонированной матрицы на комплексно-сопряженную матрицу должно давать единичную матрицу (матричную единицу), т.е.  , (3.32)где [Е] – единичная матрица, у которой все элементы главной диагонали равны 1, остальные есть 0. Матрицы, удовлетворяющие условию (3.32), в математике называются унитарными. Выясним, к чему приводит свойство унитарности матрицы 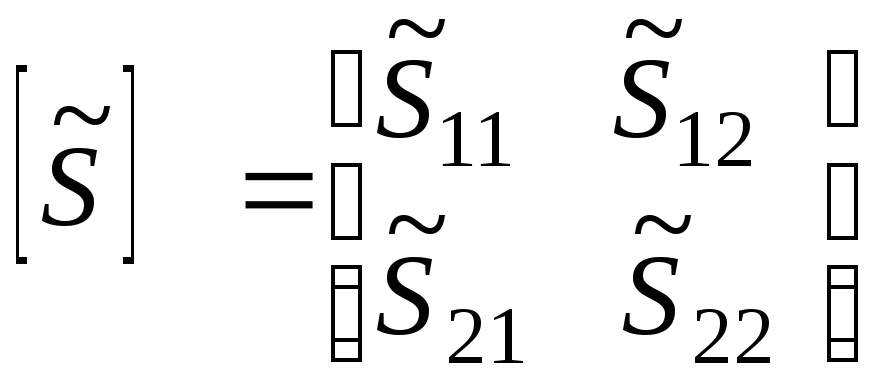 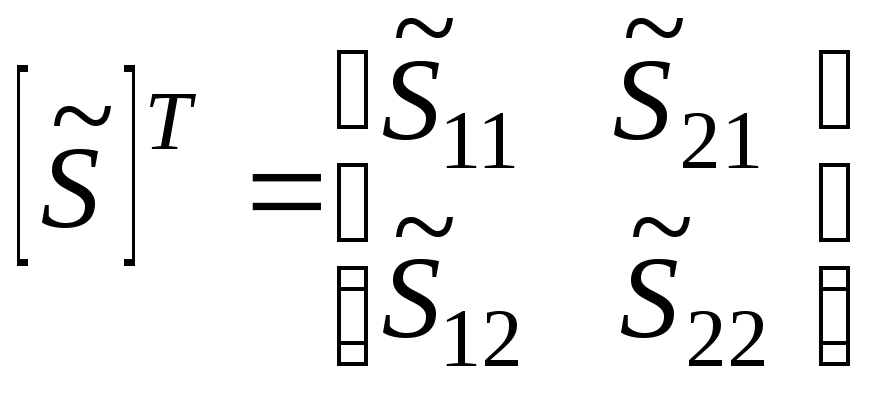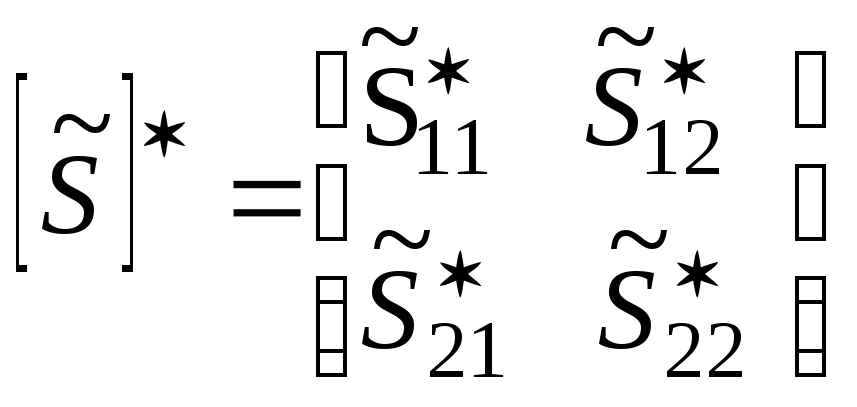на примере недиссипативного четырехполюсника. Запишем исходную, транспонированную и комплексно-сопряженную матрицы, а также условие унитарности (3.32) , , Раскрывая произведение матриц, получаем систему уравнений    (3.33)  Третье и четвертое уравнения в (3.33) тождественны, поэтому фактически имеем три независимых уравнения. Общее правило их составления можно сформулировать в виде: 1. Сумма квадратов модулей элементов каждого столбца унитарной матрицы равна 1. 2. Сумма произведений элементов одного столбца на комплексно-сопряженные элементы другого равна 0. Нетрудно видеть, что первое правило отражает закон сохранения энергии для каждого входа многополюсника при условии согласования остальных плеч. Действительно, представим, что на 1-ый вход 2N- полюсника падает мощность 1 Вт (рис.3.4), что соответствует  . Остальные плечи нагружены на свои согласованные нагрузки. Тогда очевидно т.е. сумма мощностей, уходящих от многополюсника волн, должна давать 1 Вт. 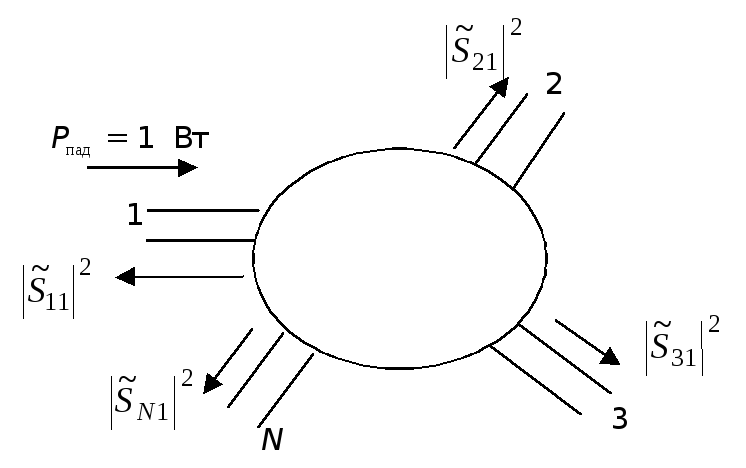 Рис.3.4 Свойство недиссипативности, так же как взаимности, в большинстве случаев является очевидным. Использование этих свойств в сочетании с использованием свойства симметрии многополюсника значительно облегчают задачу определения его матрицы . Далее мы рассмотрим применение этих общих положений теории многополюсников для анализа конкретных устройств СВЧ, разделяя их по числу полюсов (входов). |