Главная страница
Навигация по странице:

  • Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

  • Параллелограмм Определение 1.

  • Свойства параллелограмма

  • Прямоугольник Определение 1. Прямоугольником называется параллелограмм, у которого все углы прямые.

  • прямоугольником

  • Определение 1. Ромбом называется параллелограмм, у которого все стороны равны.

  • Признаки ромба ! Используя признаки ромба, можно определить, является ли данный четырёхугольник или параллелограмм ромбом.

  • Определение 1. Квадратом называется прямоугольник, у которого все стороны равны.

  • Трапеция Определение 1. Четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется трапецией .

  • Параллельные стороны трапеции называются её основаниями.

    		•

    Теория 8 класс. Теоретический материал .Выучить. Четырехугольники, 8 класс Многоугольник


    Скачать 0.83 Mb.
    НазваниеЧетырехугольники, 8 класс Многоугольник
    АнкорТеория 8 класс
    Дата15.04.2022
    Размер0.83 Mb.
    Формат файлаdocx
    Имя файлаТеоретический материал .Выучить.docx
    ТипГлава
    #476634

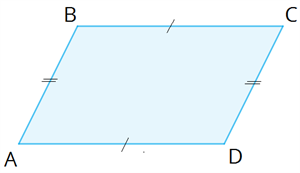
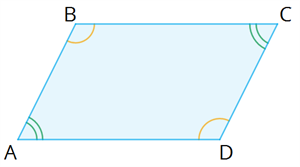
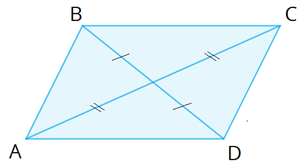
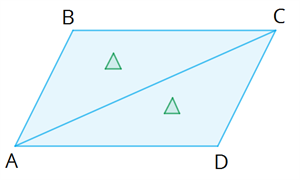
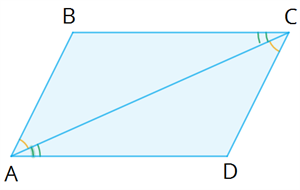
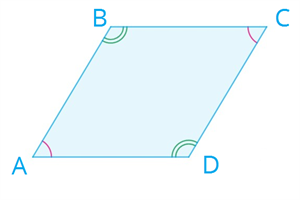
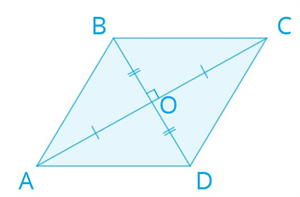
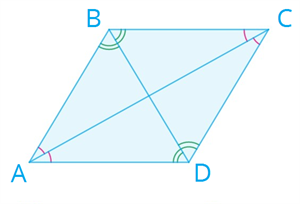
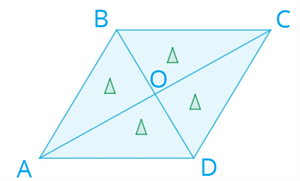
    Глава «Четырехугольники», 8 класс

    Многоугольник

    Многоугольник — это простая замкнутая ломаная линия и конечная часть плоскости, которую она ограничивает.

     

    Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

     

    Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

      

     

    A, B, C, D, E — вершины;
    AB, BC, CD, DE, AE — стороны;
    AC, AD, BE, BD, CE — диагонали.

     

    Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

     

    Пятиугольник ABCDE является выпуклым многоугольником. 

    Сумма углов выпуклого n-угольника равна 180°⋅(n−2).
    Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на 2 меньше, чем количество сторон в многоугольнике.

     

    Сумма внутренних углов любого треугольника равна 180°.

    Сумма внешних углов выпуклого многоугольника равна 360°


    Параллелограмм
    Определение 1. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
    Свойства параллелограмма

    1. Противоположные стороны параллелограмма равны:

    AB=DC,  BC=AD.


    Рис. 1. Первое свойство параллелограмма

    2. Противоположные углы параллелограмма равны:

    ∢ A= ∢ C,  ∢ B= ∢ D.


    Рис. 2. Второе свойство параллелограмма

    3. Диагонали параллелограмма точкой пересечения делятся пополам:

    BO=OD,  AO=OC.


    Рис. 3. Третье свойство параллелограмма

    4. Диагональ делит параллелограмм на два равных треугольника:

    треугольники ABC и CDA равны.


    Рис. 4. Четвёртое свойство параллелограмма

    5. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180 градусам: ∢ A + ∢ D=180°.


    Рис. 5. Пятое свойство параллелограмма

    6. Накрест лежащие углы при диагонали равны:

    ∢ BAC= ∢ ACD, ∢ BCA= ∢ CAD.


    Рис. 6. Шестое свойство параллелограмма

     



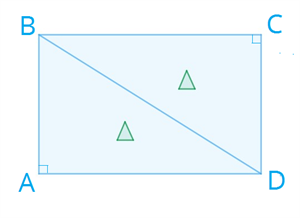
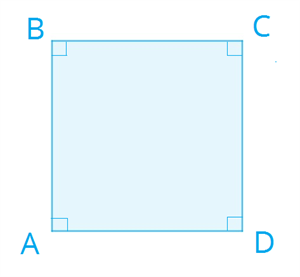
    Прямоугольник

    Определение 1. Прямоугольником называется параллелограмм, у которого все углы прямые.

     

    Свойства прямоугольника

    Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма.

     

    1. Противоположные стороны прямоугольника равны: AB=CD, BC=AD.


    2. Каждый угол прямоугольника равен 90°.


    3. Диагонали прямоугольника точкой пересечения делятся пополам: BO=OD, AO=OC.


    4. Диагональ прямоугольника делит его на два равных прямоугольных треугольника.


    5. Накрест лежащие углы при диагоналях равны.


    6. Диагонали прямоугольника равны: BD=AC.


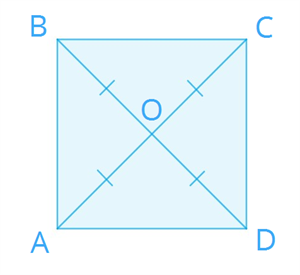
    Признаки прямоугольника

     

    ! С помощью этих признаков можно определить, является ли параллелограмм или четырёхугольник прямоугольником.
    1. Если три угла четырёхугольника прямые, то этот четырёхугольник является прямоугольником.

    2. Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.

    3. Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.

    Ромб

    Определение 1. Ромбом называется параллелограмм, у которого все стороны равны.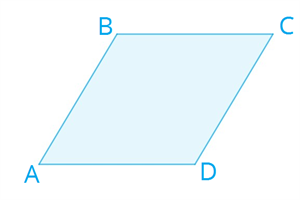



    Свойства ромба

    Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.

    1. Противоположные стороны ромба равны: AB=BC=CD=AD (т. к. все стороны равны).


    2. Противоположные углы ромба равны: ∢ A= ∢ C;   ∢ B= ∢ D.


    3. Диагонали ромба точкой пересечения делятс mn я пополам: BO=OD;   AO=OC.



    4. Сумма углов, прилежащих к одной стороне ромба, равна 180°:  ∢ A + ∢ D=180°.


    5. Диагонали ромба взаимно перпендикулярны: AC⊥ BD.


    6. Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).


    7. Диагонали делят ромб на четыре равных прямоугольных треугольника.

    Треугольники ABO, СBO, CDO, ADO — равные прямоугольные треугольники.



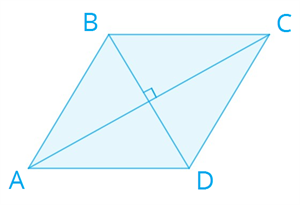
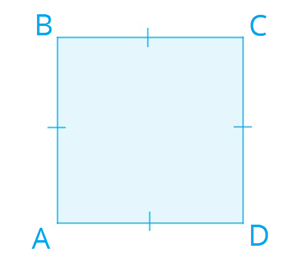
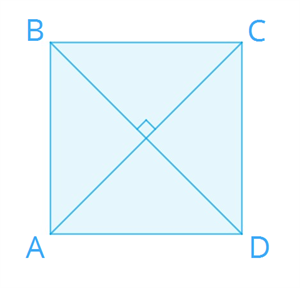
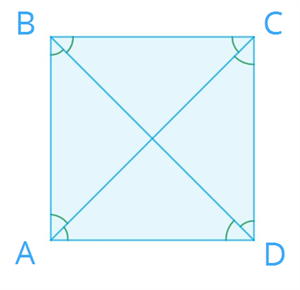
    Признаки ромба
     

    ! Используя признаки ромба, можно определить, является ли данный четырёхугольник или параллелограмм ромбом.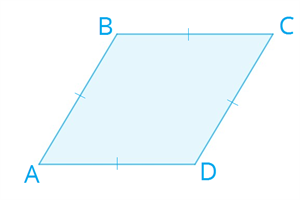

    1. Если диагонали параллелограмма перпендикулярны, то данный параллелограмм является ромбом.

    2. Если две смежные стороны параллелограмма равны, то данный параллелограмм является ромбом.

    3. Если диагонали параллелограмма являются биссектрисами его углов, то данный параллелограмм является ромбом.

    4. Если все стороны четырёхугольника равны, то данный четырёхугольник является ромбом.

    Квадрат

    Определение 1. Квадратом называется прямоугольник, у которого все стороны равны.



    Свойстваквадрата

    Квадрату присущи все свойства параллелограмма. Квадрат можно считать ромбом с прямыми углами или прямоугольником с равными сторонами, поэтому квадрат обладает всеми свойствами ромба и прямоугольника.

    1. Все стороны квадрата равны: AB=BC=CD=AD.


    2. Каждый из углов квадрата равен 90°.


    3. Диагонали квадрата равны и точкой пересечения делятся пополам: BD=AC;  BO=OD=AO=OC


    4. Диагонали квадрата взаимно перпендикулярны: BD⊥ AC.


    5. Диагонали квадрата являются биссектрисами его углов: ∢ ABD= ∢ DBC= ∢ BCA=...=45°.


    6. Диагонали квадрата делят его на четыре равных прямоугольных равнобедренных треугольника.



    Признаки квадрата

    !С помощью этих признаков можно определить, является ли прямоугольник или ромб квадратом.
    1. Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.

    2. Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.

    3. Если один из углов ромба прямой, то этот ромб является квадратом.

    4. Если диагонали ромба равны, то этот ромб является квадратом.

    Трапеция

    Определение 1. Четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется трапецией.



     

    Параллельные стороны трапеции называются её основаниями.

    AD и BC — основания.

    Стороны, которые не параллельны, называются боковыми сторонами трапеции.

    AB и CD — боковые стороны трапеции.

     

    Есть несколько видов трапеций. Чаще всего рассматриваются прямоугольные и равнобедренные трапеции.

    Прямоугольная трапеция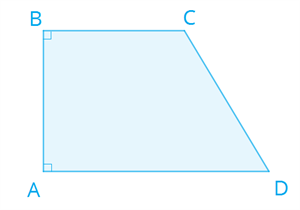



    Трапеция, у которой одна боковая сторона перпендикулярна основаниям, называется прямоугольной трапецией.

    Равнобедренная трапеция



    Трапеция, у которой боковые стороны равны, называется равнобедренной.

    Свойстватрапеции

    Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360°.

     

    Свойство, которое присуще трапеции любого вида:

    сумма углов, прилежащих к боковой стороне, равна 180°.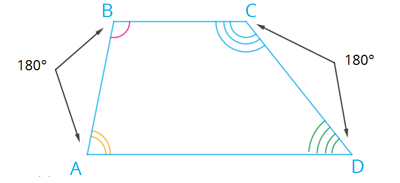

     



    Свойства, присущие только равнобедренным трапециям

    1. У равнобедренной трапеции углы при основаниях попарно равны.

    На рисунке 1 равные углы ∠A=∠D, ∠B=∠C.


    Рис. 1. Равнобедренная трапеция с равными углами

    2. Диагонали равнобедренной трапеции равны.

    На рисунке 2 равны диагонали AC=BD.


    Рис. 2. Равнобедренная трапеция с равными диагоналями

     

     

    Признаки равнобедренной трапеции

    1. Если углы при основании трапеции равны, то эта трапеция равнобедренная.

     

    2. Если диагонали трапеции равны, то эта трапеция равнобедренная.

    написать администратору сайта