Дифр.решетка отчет по Л.Р.№ 2. Чф фгаоу во пнипу
 Скачать 1.13 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Чайковский филиал федерального государственного автономного образовательного учреждения высшего образования «Пермский национальный исследовательский политехнический университет» (ЧФ ФГАОУ ВО « ПНИПУ») Кафедра автоматизации, информационных и инженерных технологий Оптика Компьютерная лабораторная работа № 2“Дифракционная решетка” Выполнил А.А. Васильева студент группы АСУ-21-1бз Принял проф. кафедры АИИТ, доктор техн. Наук Е.А. Морозов 2022 ВВЕДЕНИЕ Область исследования: Данное исследование относится к программному и компьютерному обеспечению и моделированию физических процессов. Актуальность: Программа способна смоделировать зависимость интенсивности света от разности фаз между осцилляторами, необходимость углубленного изучения оптики и компьютерного моделирования. Углубленное изучение физики. . Цель работы: Создать компьютерную модель работы дифракционной решетки. Задачи исследования: Ознакомиться с теоретической частью. Разработать компьютерную модель. Провести компьютерный эксперимент. Достоверность и обоснованность результатов: Использование проверенных фундаментальных теорий. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ Проанализируем основные моменты компьютерной модели дифракционной решетки. По идее Френеля появление максимумов и минимумов интенсивности является результатом интерференции лучей от большого числа вторичных (когерентных) источников (принципа Гюйгенса – Френеля). Для компьютерной двумерной модели, каждую щель дифракционной решетки можно рассматривать как точечный источник вторичных волн. Таким образом, нам необходимо найти суммарную интенсивность света  линейно расположенных источников в точке  на экране. Кроме того, поскольку положение точки на экране, пропорционально углу 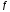 к прямой, перпендикулярной линии источников, то будем строить зависимость интенсивности непосредственно от угла 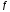. Это позволяет исключить несущественные подробности моделирования работы дифракционной решетки.Пусть имеется гармонических осцилляторов, колеблющихся с частотой 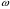 , расположенных на равных расстояниях один от другого и обладающих равными амплитудами 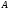 . Пусть разность фаз между осцилляторами составляет фазовый угол  . Разность фаз создается либо из-за выбора фазовых сдвигов колебаний осцилляторов, либо потому, что мы находимся под углом к линии осцилляторов. Независимо от причин возникновения фазового сдвига нам надо вычислить сумму такого вида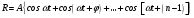 (1)Из справочника, находим сумму ряда (1) 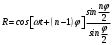 (2)Отношение 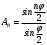 (3)очевидно, дает результирующую фазу амплитуду колебаний, как функцию фазового сдвига и количества источников. 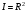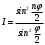Поскольку непосредственно регистрируется приборами и, в частности, глазом не величина поля, а его интенсивность  , то для амплитуды интенсивности пишем (4)ПРОГРАММНАЯ МОДЕЛЬ Вид функции интенсивности исследуем, построив компьютерный график. Используя базовую программу построения графиков функций, пишем программу: tt:=0.0001; {шаг счета} k:=5; {число осцилляторов} f:=0.0001; {сдвиг фаз между соседними осцилляторами, градусы} Fori:=1 to 200000 do begin Int:=Sqr(sin(0.5*k*f))/Sqr(sin(0.5*f)); {вычислениеинтенсивности} SetPixel(X0+round(f*40*MasX),Y0-round(Int*40*MasY), clNavy); {вправо} SetPixel(X0-round(f*40*MasX),Y0-round(Int*40*MasY), clNavy); {влево} f:=f+tt; end; 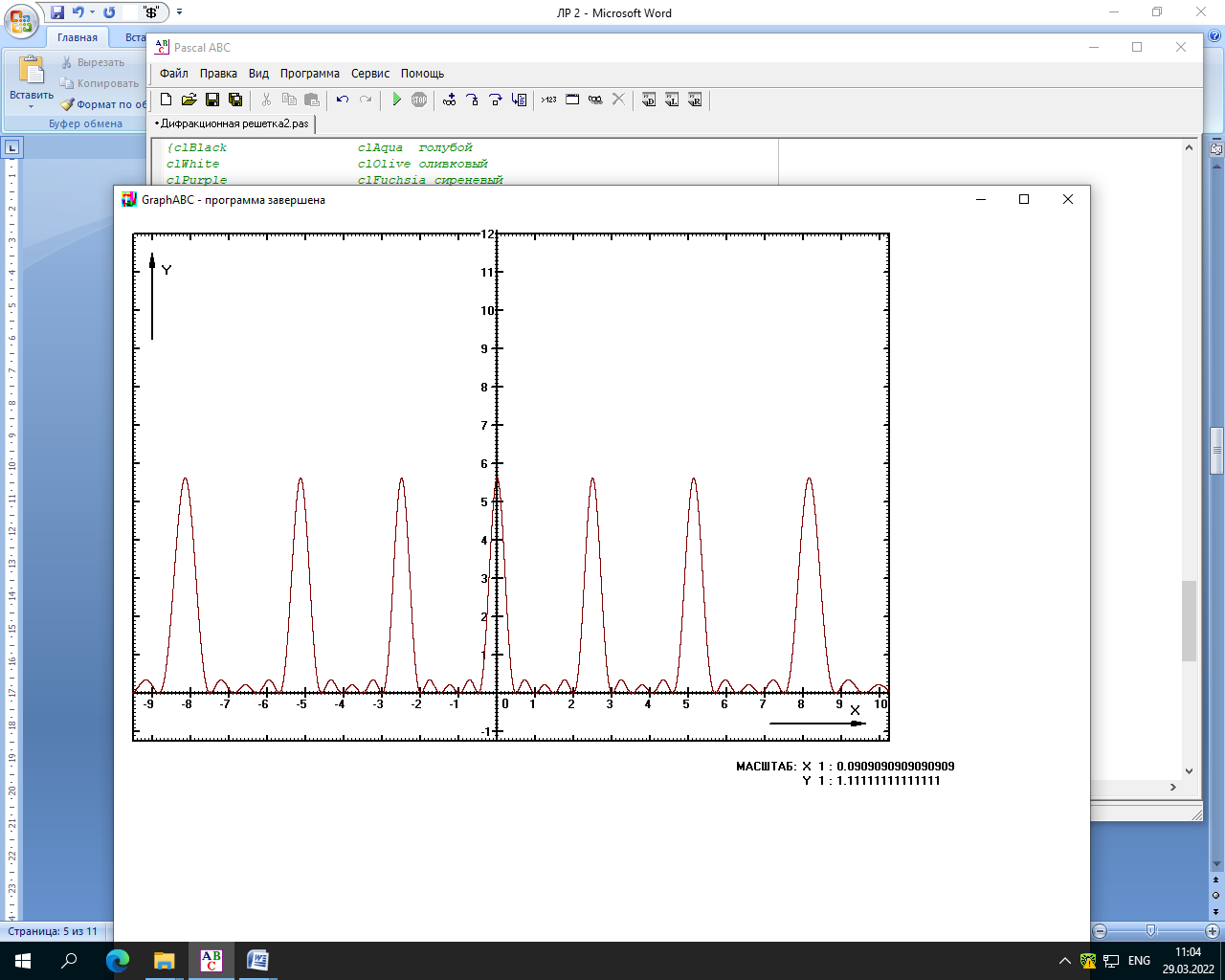 Рисунок 1 - Интенсивность колебаний при 5 осцилляторах На рисунке представлены траектории движения снаряда для случая 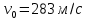 . Протестируем правильность работы программы, используя тот факт, что при одном осцилляторе (рисунок 2) выражение (4) составит 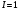 , а при двух осцилляторах (рисунок 3) . 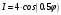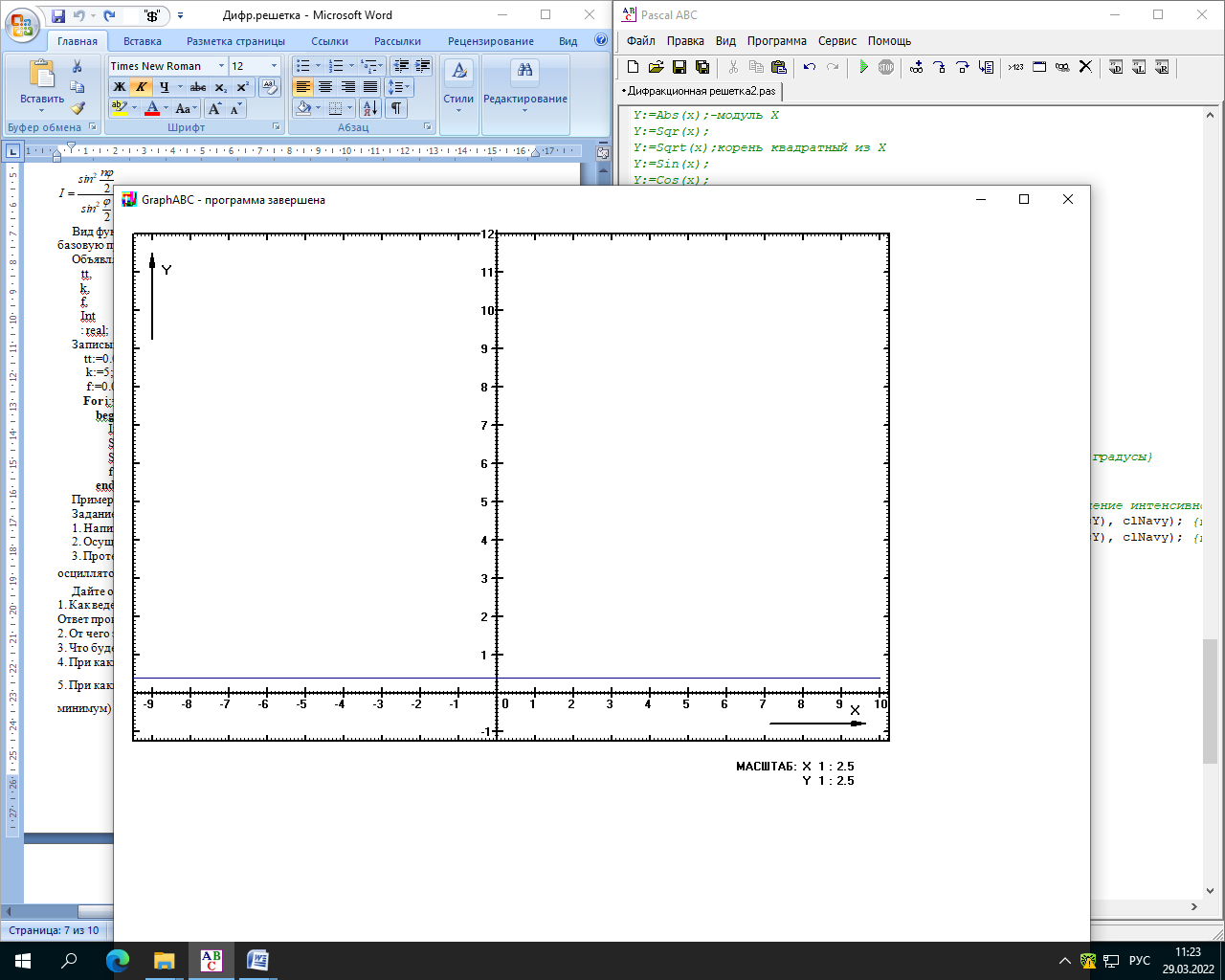Рисунок 2 - Интенсивность колебаний при 1 осцилляторе 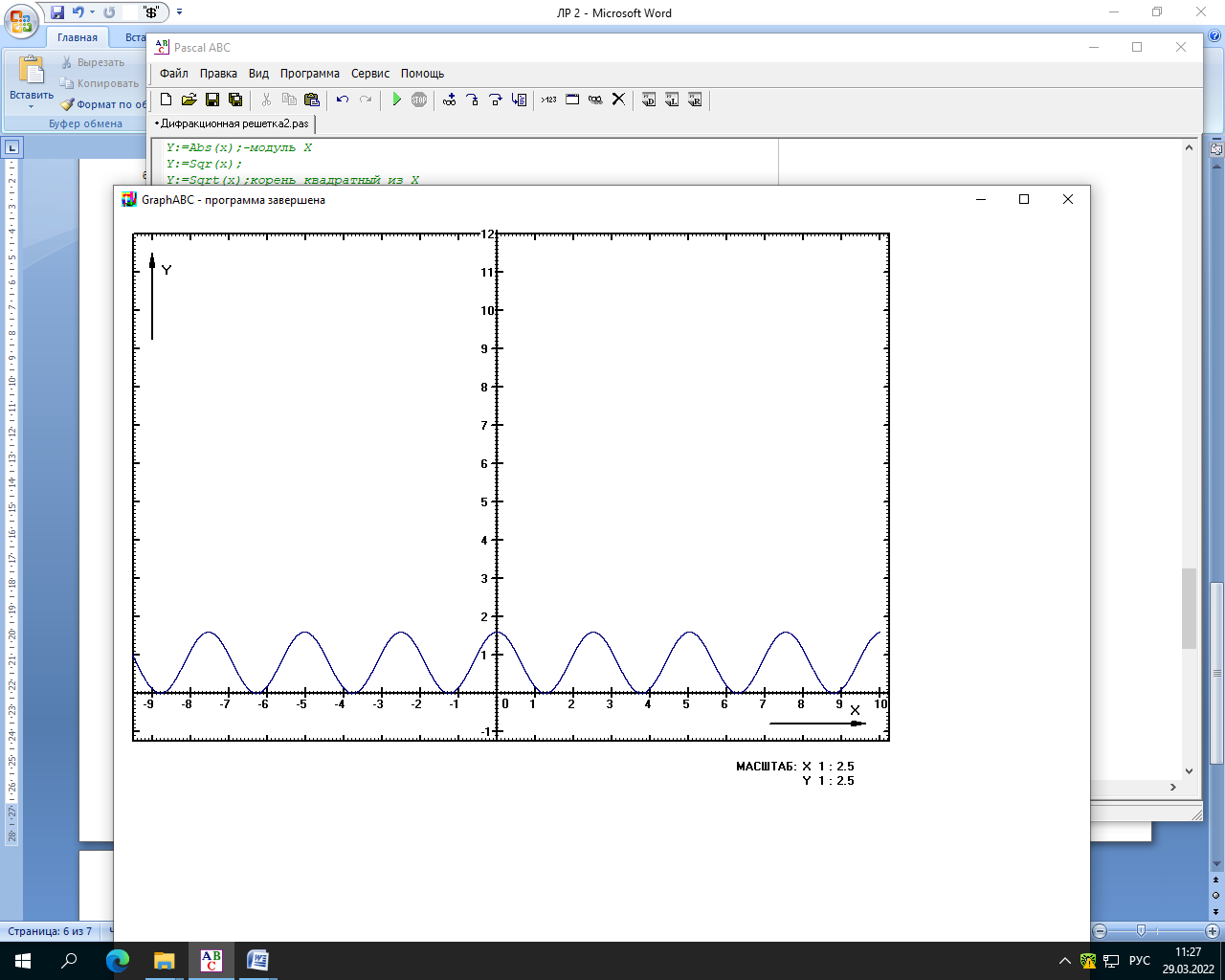 Рисунок 3 - Интенсивность колебаний при 2 осцилляторах ВОПРОСЫ: Как ведет себя функция интенсивности при увеличении количества осцилляторов? Как видно на рисунке 4 и 5, при увеличении количества осцилляторов интенсивность колебаний нарастает. 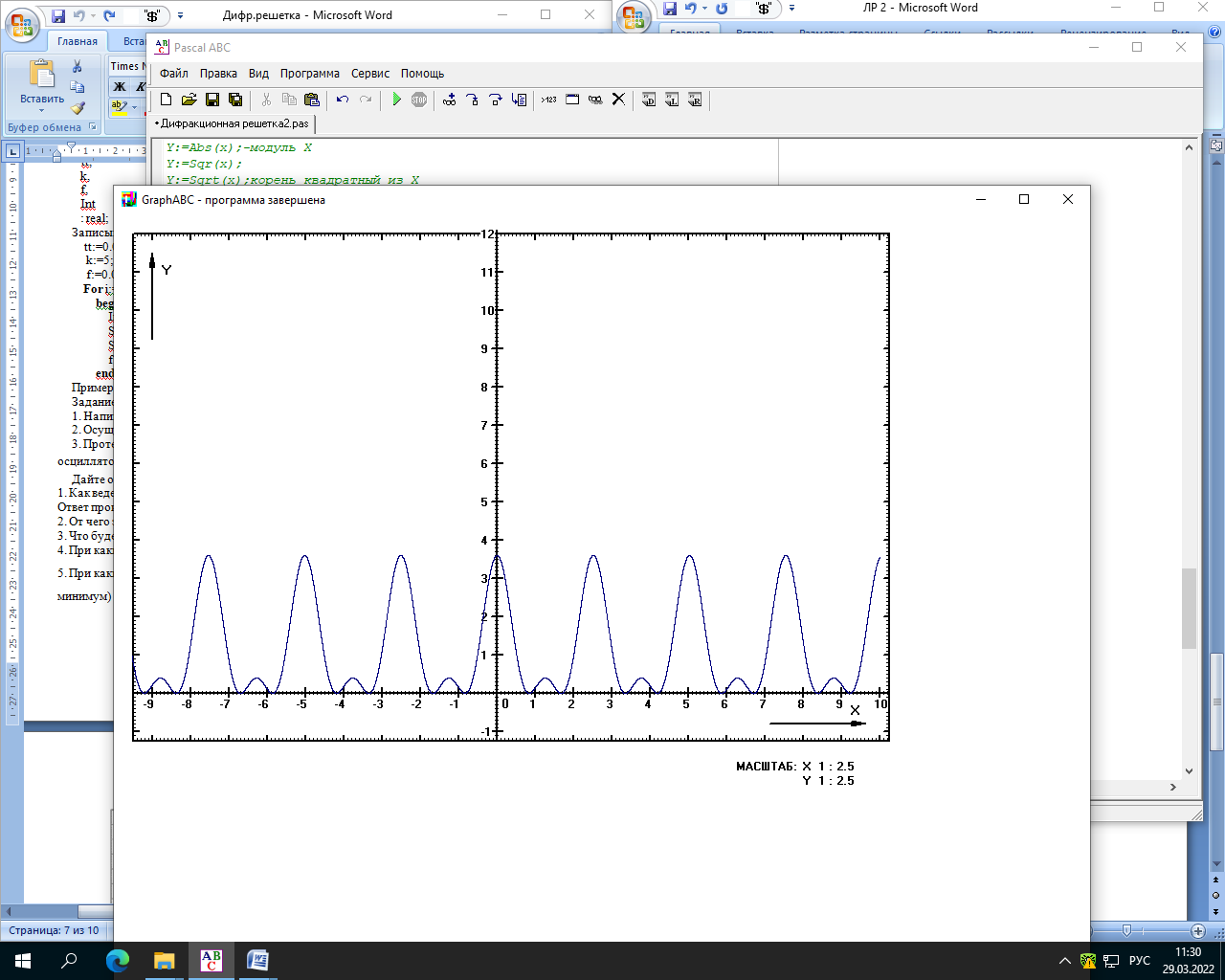 Рисунок 4 - Интенсивность колебаний при 3 осцилляторах 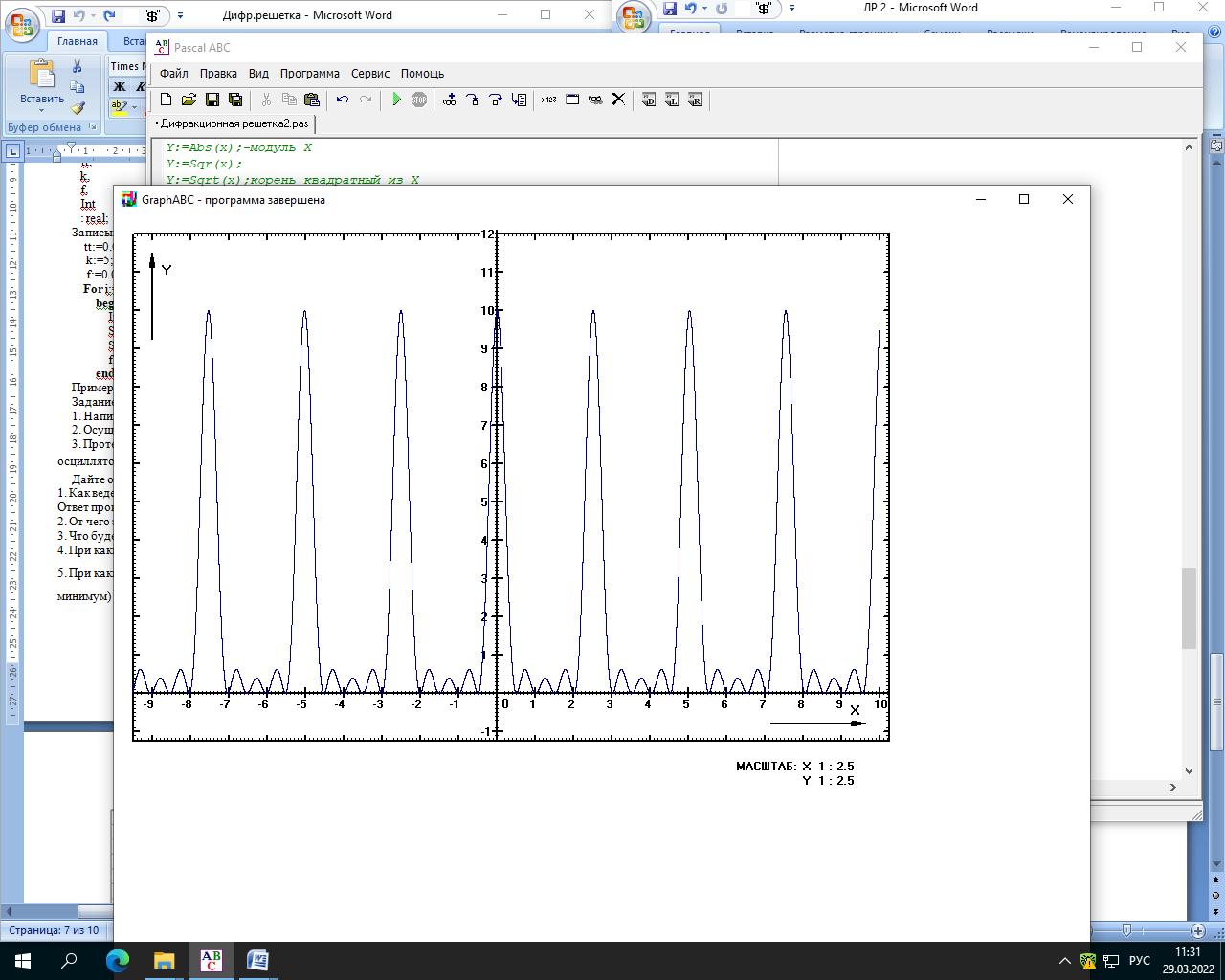 Рисунок 5 - Интенсивность колебаний при 5 осцилляторах От чего зависит количество дополнительных минимумов? Условие дополнительных минимумов: 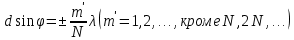 где: N –число щелей. Исходя из выше приведенной формулы, количество дополнительных минимумов зависит от количества осцилляторов Что будет если число осцилляторов будет стремится к бесконечности? Как изображено на рисунках 6,7 и 8, при увеличении количества осцилляторов, количество дополнительных максимумов и минимумов, а также амплитуда колебаний увеличиваются пропорционально. Исходя из этого вывода, можно предположить, что если число осцилляторов будет стремится к бесконечности, то число дополнительных максимумов и минимумов вместе с амплитудой также будут стремиться к бесконечности. 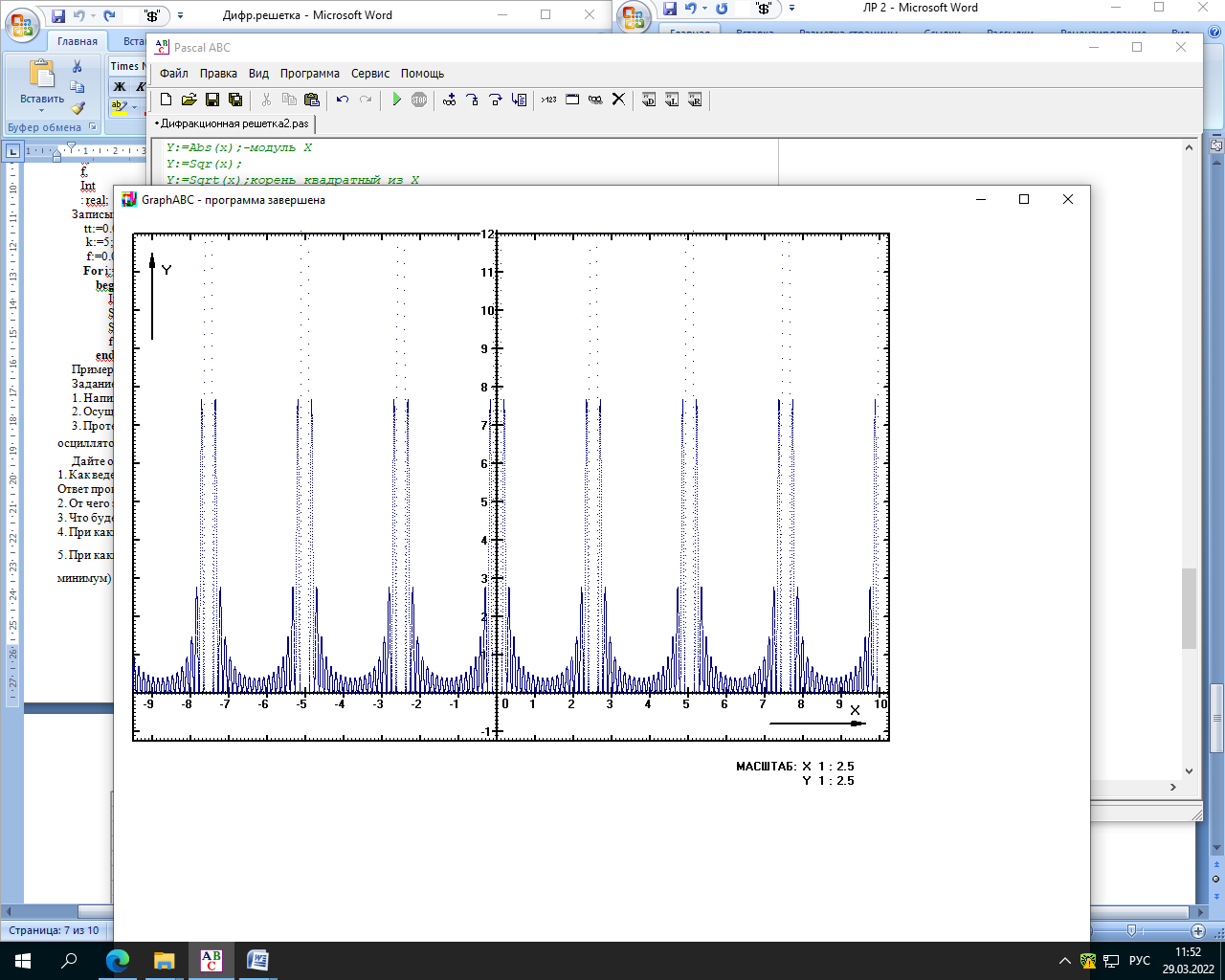 Рисунок 6 - Интенсивность колебаний при 20 осцилляторах 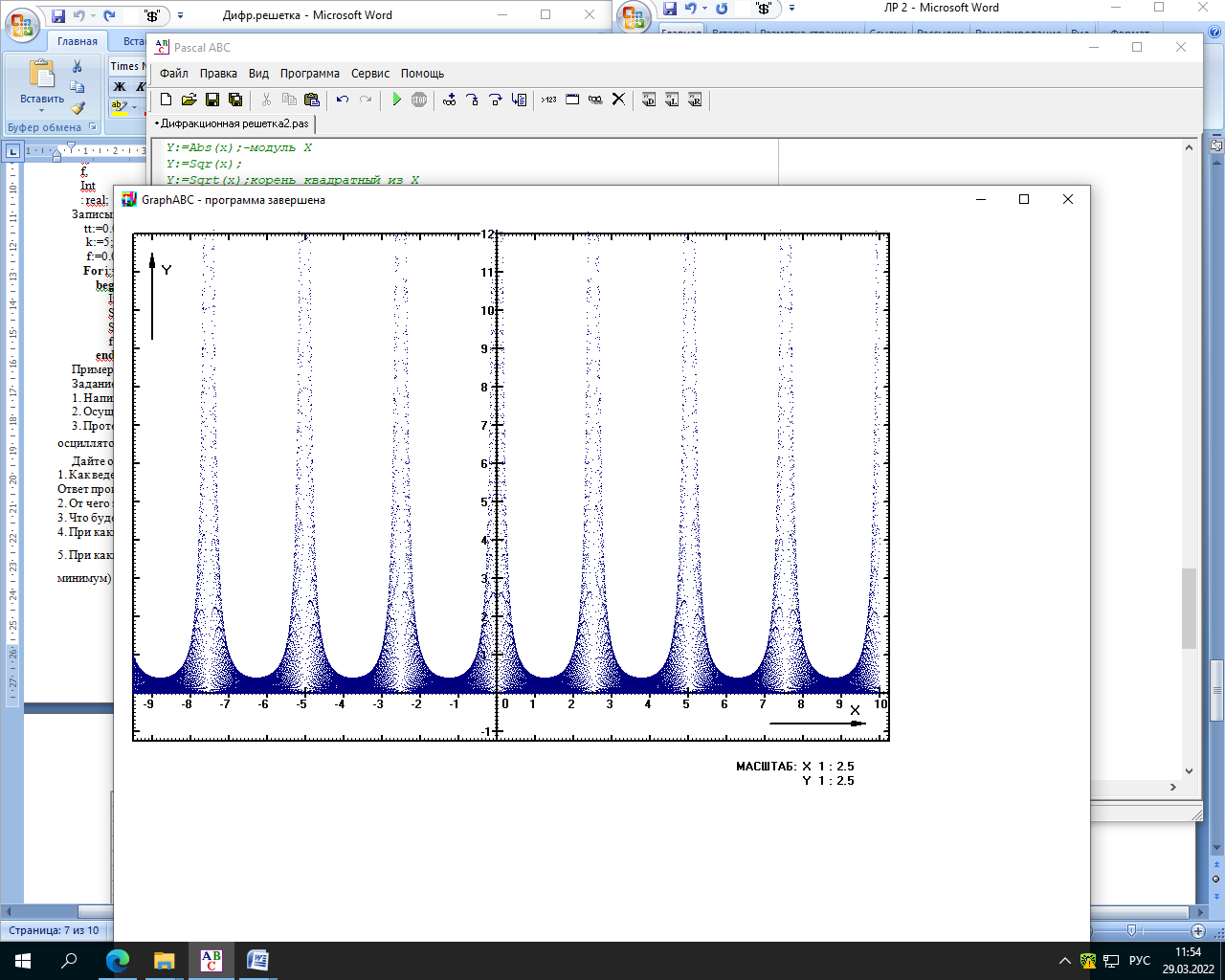 Рисунок 7 - Интенсивность колебаний при 200 осцилляторах 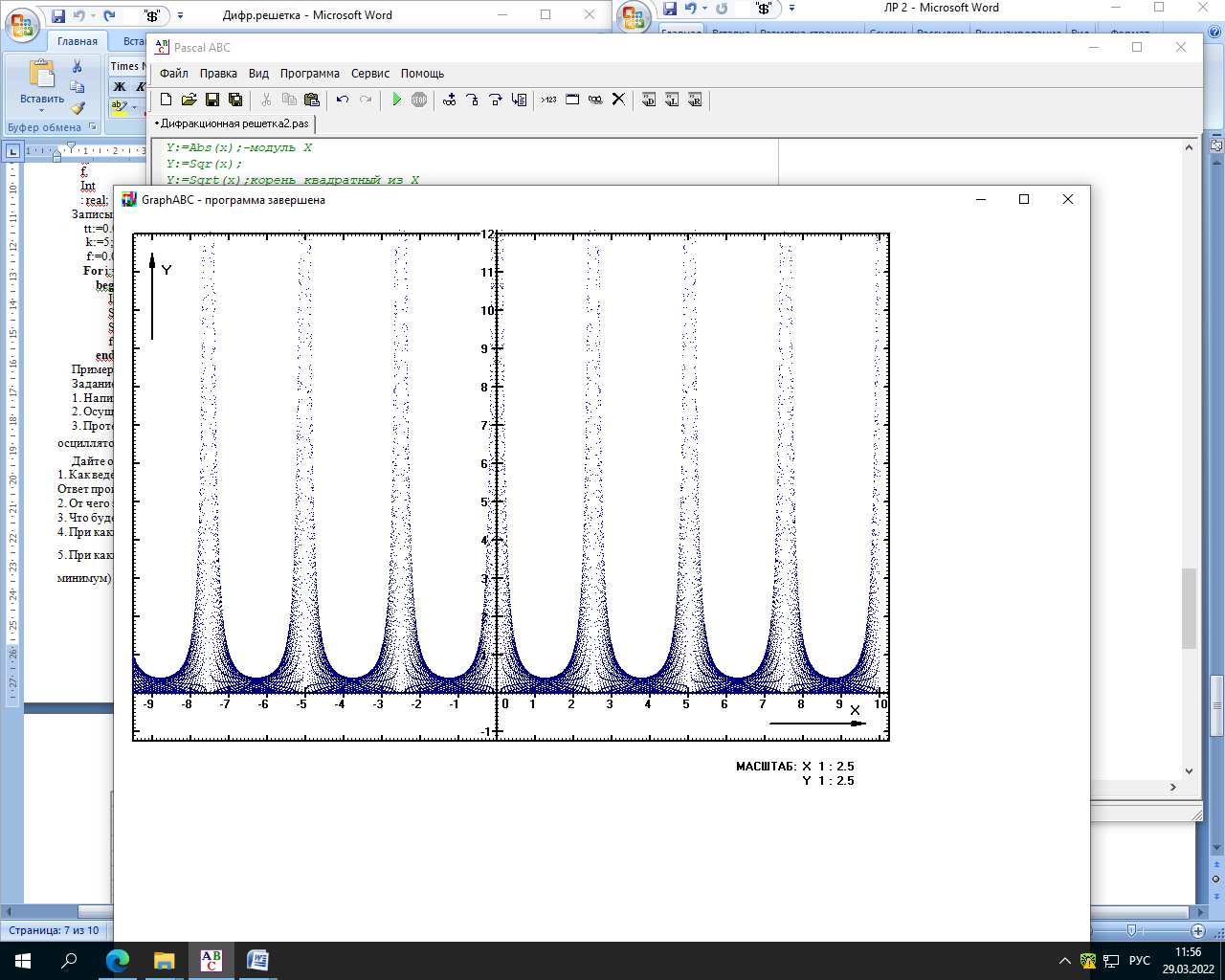 Рисунок 8 - Интенсивность колебаний при 2000 осцилляторах При каких значениях разности фаз образуются главные максимумы? (кратно 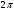 )Условие главных максимумов дифракционной решетки: 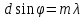 где d- период дифракционной решетки, φ – угол дифракции, m – соответствует порядку максимумов, начиная с центрального m=0, λ — длина волны падающего на решетку света. 5. При каких значениях разности фаз образуются добавочные минимумы? ( 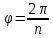 , 1 минимум)Условие дополнительных минимумов: где: N –число щелей. Теперь смоделируем работу дифракционной решетки. Для этого нам необходимо определить разность фаз двух точечных осцилляторов расположенных на расстоянии  друг от друга. В нашем приближении мы пренебрегаем шириной источников осцилляторов. Как видно из рисунка 2, разность фаз волн обоих источников равна числу волн заключенных на отрезке  , умноженному на . Поэтому разность фаз двух источников равна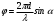 ..(5)Подставляя разность фаз в выражение (4) получим зависимость интенсивности от угла наблюдения 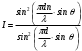 .Доработаем имеющуюся у нас программу интенсивности. Объявляем тип переменных. tt, {шаг счета} k, {число осцилляторов или число щелей ршетки} f, {сдвиг фаз между осцилляторами} a, {угол наблюдения} d, {расстояние между щелями или период решетки} L, {длина волны света} Int {суммарная интенсивность} : real; Расширяем блок построения графика интенсивности. {Блок расчета зависимости интенсивности света от угла наблюдения после прохождения дифракционной решетки} tt:=0.00001; {шаг счета} k:=20; {число осцилляторов или щелей решетки} d:=0.001/300; {период решетки в метрах (300 трихов на миллиметр)} L:=575/1000000000; {длина волны в метрах, зеленый свет} a:=0.0001; {угол, радианы} Fori:=1 to 200000 do begin f:=(2*Pi*d/l)*sin(a); {вычисление разности фаз источников} Int:=Sqr(sin(0.5*k*f))/Sqr(sin(0.5*f)); {вычисление интенсивности} SetPixel(X0+round(f*40*MasX),Y0-round(Int*40*MasY), clGreen); {вправо} SetPixel(X0-round(f*40*MasX),Y0-round(Int*40*MasY), clGreen); {влево} a:=a+tt; {изменение угла наблюдения} end; ВОПРОСЫ: Как расположены максимумы света различных длин волн относительно друг друга? В центре все световые волны накладываются друг на друга, и по мере удаления от центра смещаются относительно друг друга все больше и больше. 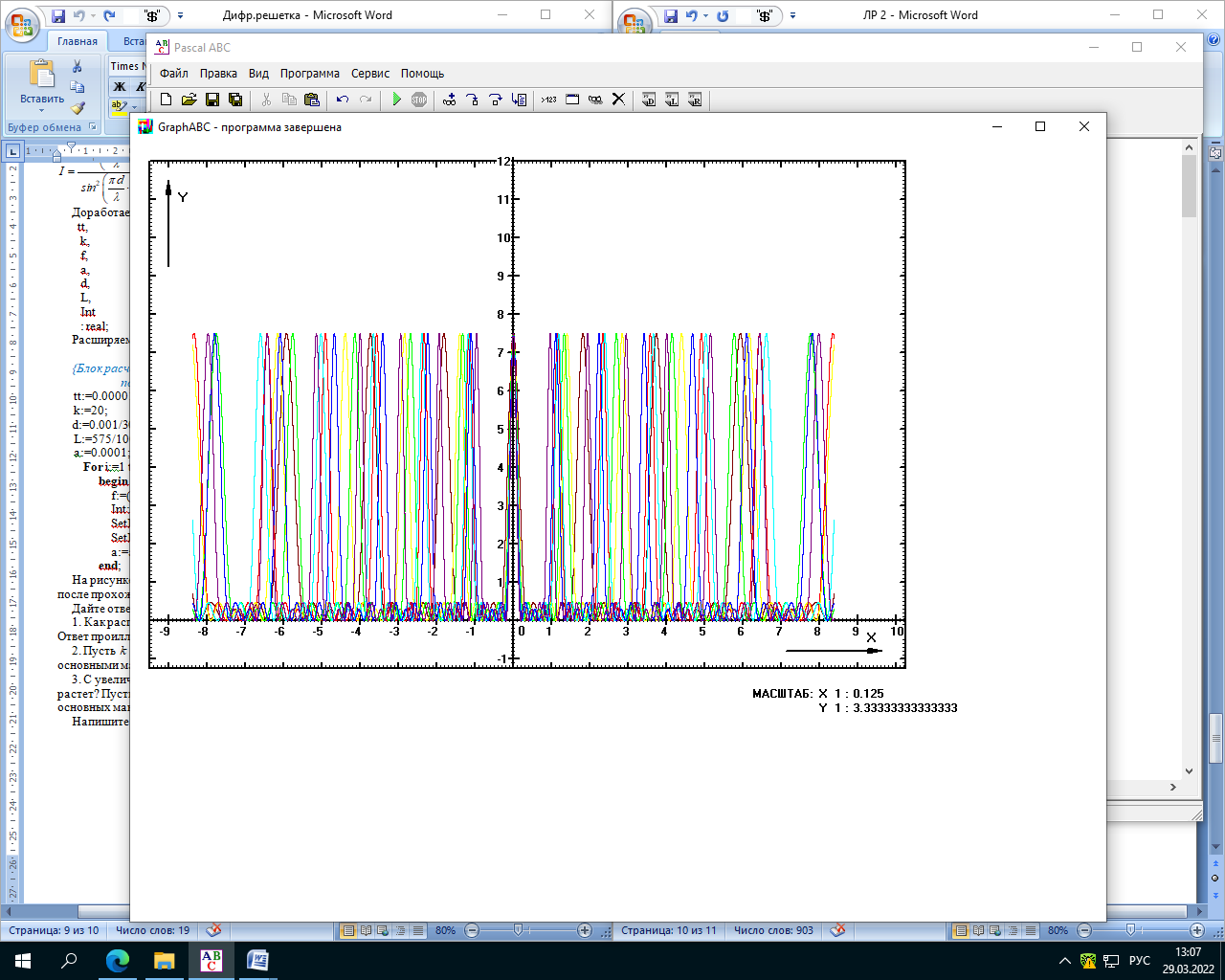 Рисунок 9 - Интенсивность колебаний при 5 осцилляторах различных световых спектров Пусть  число щелей решетки. Сколько добавочных минимумов возникает между основными максимумами. Условие дополнительных минимумов: 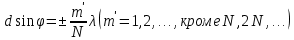где: N –число щелей. С увеличением числа щелей интенсивность основных максимумов растет. Как она растет? Пусть число щелей увеличились в 3 раза. Во сколько раз возрастет интенсивность основных максимумов. Зависимость интенсивности главных максимумов: 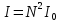 Пускай количество осцилляторов равняется 5, тогда 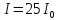 Следовательно, если количество осцилляторов увеличить в 3 раза, т.е. 5*3, тогда 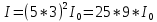 Интенсивность основных максимумов возрастет в: 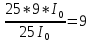 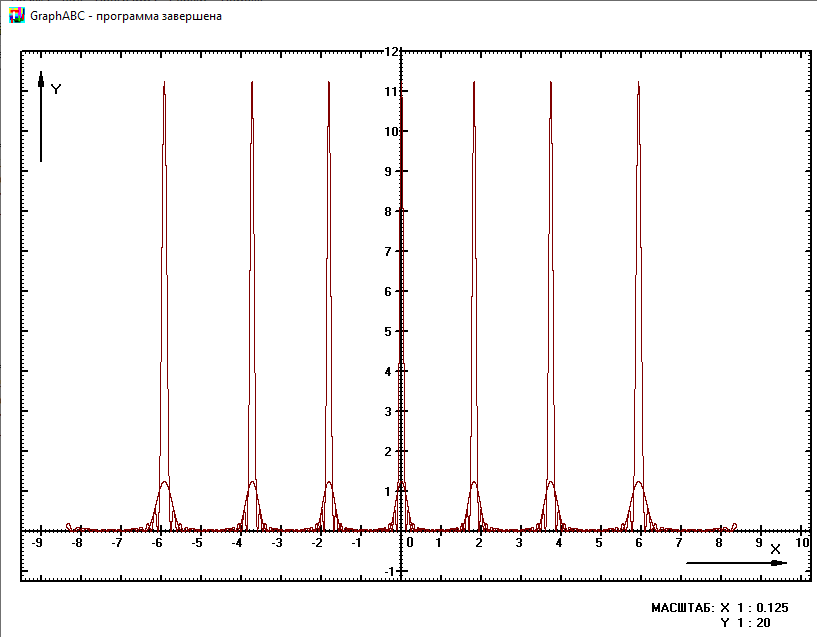 Рисунок 10 - Интенсивность колебаний при 5 и 15 осцилляторах ЗАКЛЮЧЕНИЕ В результате выполнения работы были решены такие задачи: Ознакомилась с теоретической частью. Разработала компьютерную модель. Провела компьютерный эксперимент. Вследствие чего была выполнена цель: Создана компьютерная модель дифракционной решетки. |