Курсовая работа Числа Фиббоначи. курсовая Числа фиббоначчи. Числа Фибоначчи

Название	Числа Фибоначчи
Анкор	Курсовая работа Числа Фиббоначи
Дата	28.02.2022
Размер	1.14 Mb.
Формат файла
Имя файла	курсовая Числа фиббоначчи.docx
Тип	Курсовая #377101

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КАРЕЛЬСКАЯ ГОСУДАРСТВЕННАЯ ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ»

Факультет начального образования

КУРСОВАЯ РАБОТА

на тему

Числа Фибоначчи.

Работу выполнила

студентка 231 группы

Ляккоева Арина Михайловна

Научный руководитель:

Марченко Т. С.

К.П.Н., доцент

Оценка: ____________
«__» _______________ 2012 г.

Петрозаводск

2012

Содержание

Введение ………………………………………………………………………………………..3

Глава 1. Теоретические аспекты чисел Фибоначчи

Леонардо Фибоначчи - создатель чисел Фибоначчи………………………………….4
Числа Фибоначчи и их свойства………………………...………………………………4
Золотое сечение……………………………………………………………………………6
Примеры чисел Фибоначчи в природе…………………………………………………...8

Глава 2. Практическая часть………………………………………………………………..12

Заключение………………………………………………………………………………..……14

Литература…………………………………………………………………………………...15

Введение.

В элементарной математике существует много задач, часто трудных и интересных, которые не связаны с чьим-либо именем, а скорее носят характер своего рода «математического фольклора». Эти задачи нередко имеют хождение в нескольких вариантах; иногда несколько таких задач объединяют в одну, более сложную; иногда, наоборот, одна задача распадается на несколько более простых; словом, часто, оказывается, трудно различить, где кончается одна задача и начинается другая. Правильнее всего было бы считать, что в каждой из таких задач мы имеем дело с маленькими математическими теориями, имеющими свою историю, свою проблематику и свои методы – все это, разумеется, тесно связано с историей, проблематикой и методами «большой математики.
    Такой теорией являются и теория чисел Фибоначчи. Выросшие из знаменитой «задачи о кроликах», имеющей более семисот пятидесятилетнюю давность, числа Фибоначчи до сих пор остаются одной из самых увлекательных глав элементарной математики.
    Кроме того, и это являются фундаментальным фактом истории математики нашего времени, существенно сместился центр математических исследований в целом. В частности, утратила свои доминирующие позиции теория чисел, и резко повысился удельный вес экстремальных задач. В самостоятельную отрасль математики сложилась теория игр. По существу возникла вычислительная математика.
    Наконец было установлено довольно большое количества ранее неизвестных свойств чисел Фибоначчи, а к самим числам существенно возрос интерес.

Эта тема приобрела актуальность в связи с ростом значения комбинаторики и проблем, связанных с целыми числами. Числа из последовательности Фибоначчи встречаются в реальной жизни, они окружают нас в явлениях природы, архитектуры и т. д.

Цель: изучить последовательность чисел Фибоначчи и их свойства

Задачи: - познакомиться с литературой по данной теме

- найти примеры последовательности в реальной жизни

- решить ряд задач по данной теме

Глава 1. Теоретические аспекты чисел Фибоначчи в математике.

Леонардо Фибоначчи – создатель чисел Фибоначчи.

Итальянский купец Леонардо из Пизы (1180-1240), более известный под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
     Жизнь и научная карьера Леонарда теснейшим образом связана с развитием европейской культуры и науки.
     В век Фибоначчи возрождение было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих 2, который вместо рыцарских турниров культивировал гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами.
     На таких турнирах и заблистал талант Леонарда Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купец Боначчи, взявший его с собой на Восток и приставивший к нему арабских учителей.
     Впоследствии Фибоначчи пользовался неизменным покровительством Фридриха II.
Это покровительство стимулировало выпуск научных трактатов Фибоначчи:
обширнейшей "Книге абака", написанной в 1202 году, но дошедшей до нас во втором своем варианте, который относится к 1228 г.; "Практики геометрии"(1220г.); "Книги квадратов"(1225г.). По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику, чуть ли не до времен Декарта (17 в).

Наибольший интерес представляет сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течении нескольких следующих столетий. 1,1,2,3,5,8,13,21,34,55,89,144,233,377,
В честь автора этой задачи про кроликов вся последовательность при u1=u2=1 называется рядом Фибоначчи, а члены её - числами Фибоначчи.
Также в этом труде содержалось множество других задач. Л. Фибоначчи неоднократно путешествовал по странам Востока и в своей книге использовал труды арабских математиков.

Числа Фибоначчи и их свойства.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

В которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи). Иногда число 0 не рассматривается как член последовательности.

Более формально, последовательность чисел Фибоначчи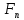

задается линейным рекуррентным соотношением:

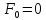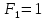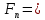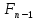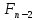, n  2

Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: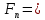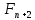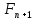

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко заметить, что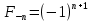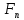

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

Числовая последовательность Фибоначчи имеет много интересных свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.

Одно из самых главных следствий этих свойств различных членов последовательности определяются следующим образом:

Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ), и мы поговорим о нем подробнее немного позже.
При делении каждого числа на следующее за ним через одно получаем число 0.382; наоборот – соответственно 2.618.
Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236. упомянем также 0.5 (1/2). Все они играют особую роль в природе, и в частности – в техническом анализе.
Интересно так же, что числа Фибоначчи периодичны, так например, каждое третье число четно, каждое четвертое число делится на 3, а каждое пятнадцатое оканчивается нулём.

Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.

Например, число 0.618 представляет собой постоянный коэффициент в так называемом золотом сечении (рис.1), где любой отрезок делится таким образом, что соотношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком. Таким образом, число 0.618 известно еще как золотой коэффициент или золотая середина. Такого типа пропорцию можно встретить абсолютно везде (рис.1).

Рис 1. Золотое сечение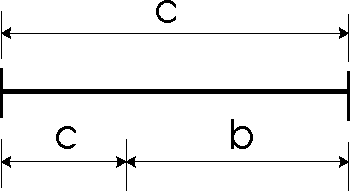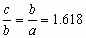

Золотое сечение.

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью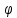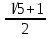

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» был введён в обиход Мартином Омом в 1835 году.

В математике пропорцией (лат. proportio) называют равенство двух отношений:a : b = c : d.

Отрезок прямой АВ можно разделить на две части следующими способами:

на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a : b = b : c или с : b = b : а.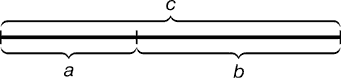

Рис.2. Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.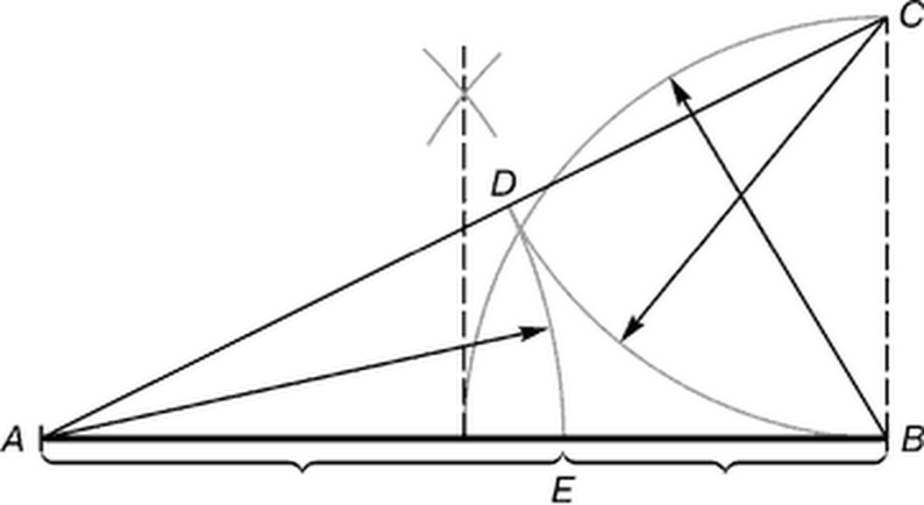

Рис. 3. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x² – x – 1 = 0.

Решение этого уравнения: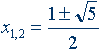

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.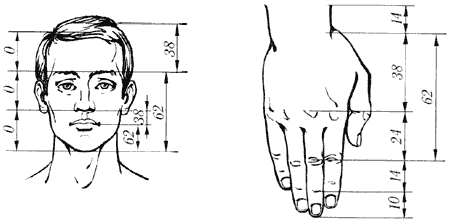

Рис. 4. Золотые пропорции в частях тела человека

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отнош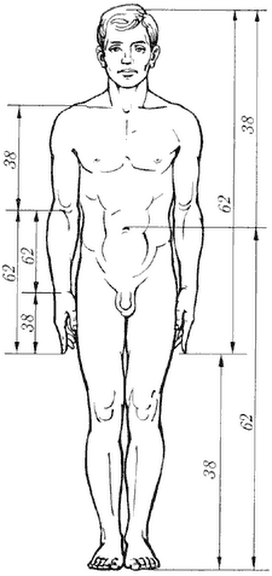

ения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Рис. 5. Золотые пропорции в фигуре человека

Примеры чисел Фибоначчи в природе.

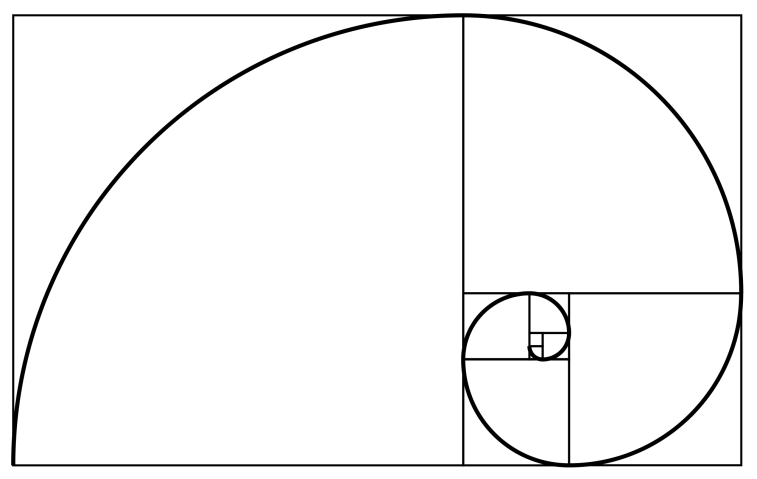Рис. 6. Спираль Фибоначчи

Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидных расположениях мелких частей мелких частей растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи.
Так взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие слева снизу направо вверх.

Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи. В семенах подсолнуха число спиралей равно 34 и 55, или 89 и 144.

Рис. 7. Семена Подсолнуха

Рис. 8.Шишка сосны.

Также числа Фибоначчи можно увидеть в размещении на побеге листьев тех или иных пород деревьев, то есть черенки листьев примыкают к стеблю по спирали, которая проходит между двумя соседнимилистьями, на пример, 1/3 полного оборота у орешника, 2/5 у дуба, 3/8 у тополя и 5/13 у ивы.

Даже развитие человека происходит по числам Фибоначчи, так на пример, в 1 год ребенок овладел ходьбой и осваивает ближайшее окружение, познаёт мир руками;в 2 года понимает речь и действует, пользуясь словесными указаниями; в 3 года действует посредством слова, задает вопросы; и т.д.

Более того спираль Фибоначчи можно увидеть в стихийных бедствиях, на пример, смерч.

Рис. 9. Смерч

Ураган тоже закручивается спиралью. Примером может быть и тысячелистник. Складывая его старые и новые ветви можно увидеть последовательность Фибоначчи.

Рис. 10. Ветви тысячелистника.

Если пересчитать лепестки некоторых наиболее распространенных цветов, - например, ириса с его 3 лепестками, первоцвета с 5 лепестками, крестовника с 13 лепестками, маргаритки с 34 лепестками и астры с 55 (и 89) лепестками, то и тут видна последовательность Фибоначчи. Спираль Фибоначчи можно увидеть даже в самых обычных морских раковинах. Но самый потрясающий пример находится прямо над нашей головой на расстоянии приблизительно в 100 000 световых лет - даже спирали галактик сформированы по абсолютно тому же принципу, как и та крошечная раковина...

Рис. 11. Солнечная система.

Есть предположение, что последовательность Фибоначчи - это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда.

Вывод: Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Глава 2. Практическая часть.

Задача о кроликах.

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Сколько пар кроликов в один год от одной пары рождается?

Решение:

1 месяц: 1+1=2

2 месяц: 2+1=3 (т.к.1 пара не может давать потомство)

3 месяц: 3+2=5 (т.к. 2 пары будут давать потомство)

4 месяц: 3+3+2=8 (т.к. 3 пары будут давать потомство)

5 месяц: 8+5=13(т.к. 5 пар будут давать потомство)

6 месяц: 13+8=21(т.к. 8 пар будут давать потомство)

7 месяц: 21+13=34(т.к. 13 пар будут давать потомство)

8 месяц: 34+21=55(т.к. 21 пара будет давать потомство)

9 месяц: 55+34=89(т.к. 34 пары будут давать потомство)

10 месяц: 89+55=144(т.к. 55 пар будут давать потомство)

11 месяц: 144+89=233(т.к. 89 пар будут давать потомство)

12 месяц: 233+144=377(т.к. 144 пары будут давать потомство)

Ответ: 377 пар кроликов будет через год

Задача о лестнице

Когда мы поднимаемся по лестнице, то каждый шаг мы делаем на следующую ступеньку или перешагнем через одну ступеньку. Сколькими способами мы можем поднятся на лестницу из 10 ступенек?

Решение:

Если у лестницы 1 ступенька, то 1 способ. Если 2 ступеньки, то 2 способа. Если 3 ступеньки, то 3 способа. 4 ступеньки, то 5 способов (т.к. на четвертую ступеньку можно встать либо со 2, либо с 3)  количество способов попасть на 4 ступеньку, складываются из кол-ва способов с 2 и 3 ступенек, т.е. кол-во способов, чтобы попасть на некоторую ступеньку равно сумме числа способов попасть на предыдущую и предпредыдущую ступеньку.

1ст. 2ст. 3ст. 4ст. 5 ст. 6 ст. 7ст. 8 ст. 9 ст. 10 ст.

1, 2, 3, 5, 8, 13, 21, 34, 55, 89сп.

Ответ: 89 способов.

Задача о золотом сечении.

Постройте золотое сечение отрезка АВ, длинной 22 см.

Заключение.

Целью курсовой работы было изучение последовательности чисел Фибоначчи и их свойств. Все задачи были реализованы. Мною были рассмотрены основные теоретические вопросы, касающиеся чисел Фибоначчи, были решены практические задачи.

В курсовой работе была показана связь чисел Фибоначчи с другими отраслями знаний.

Числа Фибоначчи являются фундаментальным фактом истории математики нашего времени, существенно сместился центр математических исследований в целом. В частности, утратила свои доминирующие позиции теория чисел, и резко повысился удельный вес экстремальных задач. В самостоятельную отрасль математики сложилась теория игр. По существу возникла вычислительная математика.

Числа Фибоначчи были исследованы многими учёными, по этой теме существует много публикаций, что, на мой взгляд, доказывает значимость этих чисел не только для математики, но и для других отраслей.

Список литературы:

Воробьев Н.Н "Числа Фибоначчи"/ Н.Н. Воробьев. - М.: "Наука", 1983г. – с. 7-11 и 94-101
Рошаль В.М. Энциклопедия символов / В.М. Рошаль – Москва: АСТ, 2006. – 107 с.
Савин А.П. Энциклопедический словарь юного математика/ А.П. Савин. – М., Педагогика, 1999г. – с. 322
Савин А.П., Станцо В.В., Котова А.Ю. Я познаю мир. Математика./ А.П. Савин, В.В. Станцо, А.Ю. Котова. – М., АСТ, 1998г. – с. 102
Якушева и др. Большая математическая энциклопедия/ Якушева и др. – М., ОЛМА-ПРЕСС, 2004г. – с. 197
Березин В. Филлотаксис и последовательность Фибоначчи/ В. Березин// Квант. -№5, 1979. – с. 53
Яглом И.М. Итальянский купец Леонардо Фибоначчи и его кролики/ И.М. Яглом // Квант. - №7, 1984. – с.15

Защита курсовой.

Цель: изучить последовательность чисел Фибоначчи и их свойства

Задачи: - познакомиться с литературой по данной теме

- найти примеры последовательности в реальной жизни

- решить ряд задач по данной теме

Итальянский купец Леонардо из Пизы (1180-1240), более известный под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
Наибольший интерес представляет сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течении нескольких следующих столетий. 1,1,2,3,5,8,13,21,34,55,89,144,233,377,
В честь автора этой задачи про кроликов вся последовательность при u1=u2=1 называется рядом Фибоначчи, а члены её - числами Фибоначчи.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

В которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи). Иногда число 0 не рассматривается как член последовательности.

Числовая последовательность Фибоначчи имеет много интересных свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.

Одно из самых главных следствий этих свойств различных членов последовательности определяются следующим образом:

Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ), и мы поговорим о нем подробнее немного позже.
При делении каждого числа на следующее за ним через одно получаем число 0.382; наоборот – соответственно 2.618.
Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236. упомянем также 0.5 (1/2). Все они играют особую роль в природе, и в частности – в техническом анализе.
Интересно так же, что числа Фибоначчи периодичны, так например, каждое третье число четно, каждое четвертое число делится на 3, а каждое пятнадцатое оканчивается нулём.

Где только не возникают числа Фибоначчи! У них есть красивые геометрические применения, важные приложения в биологии растений и т.д. особенно часто встречаются так называемые спирали Фибоначчи.

Прямоугольник с пропорциями золотого сечения называется идеальный прямоугольник или золотой прямоугольник. Если его разбить на более мелкие прямоугольники в точной последовательности Фибоначчи, а потом каждый из них разделить в таких пропорциях еще и еще, то получится система, которая называется спираль Фибоначчи.
Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи.

Есть предположение, что последовательность Фибоначчи - это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда.

Вывод: Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Задача о лестнице

Когда мы поднимаемся по лестнице, то каждый шаг мы делаем на следующую ступеньку или перешагнем через одну ступеньку. Сколькими способами мы можем поднятся на лестницу из 10 ступенек?

Решение:

Если у лестницы 1 ступенька, то 1 способ. Если 2 ступеньки, то 2 способа. Если 3 ступеньки, то 3 способа. 4 ступеньки, то 5 способов (т.к. на четвертую ступеньку можно встать либо со 2, либо с 3)  количество способов попасть на 4 ступеньку, складываются из кол-ва способов с 2 и 3 ступенек, т.е. кол-во способов, чтобы попасть на некоторую ступеньку равно сумме числа способов попасть на предыдущую и предпредыдущую ступеньку.

1ст. 2ст. 3ст. 4ст. 5 ст. 6 ст. 7ст. 8 ст. 9 ст. 10 ст.

1, 2, 3, 5, 8, 13, 21, 34, 55, 89сп.

Курсовая работа Числа Фиббоначи. курсовая Числа фиббоначчи. Числа Фибоначчи

Содержание

Введение ………………………………………………………………………………………..3