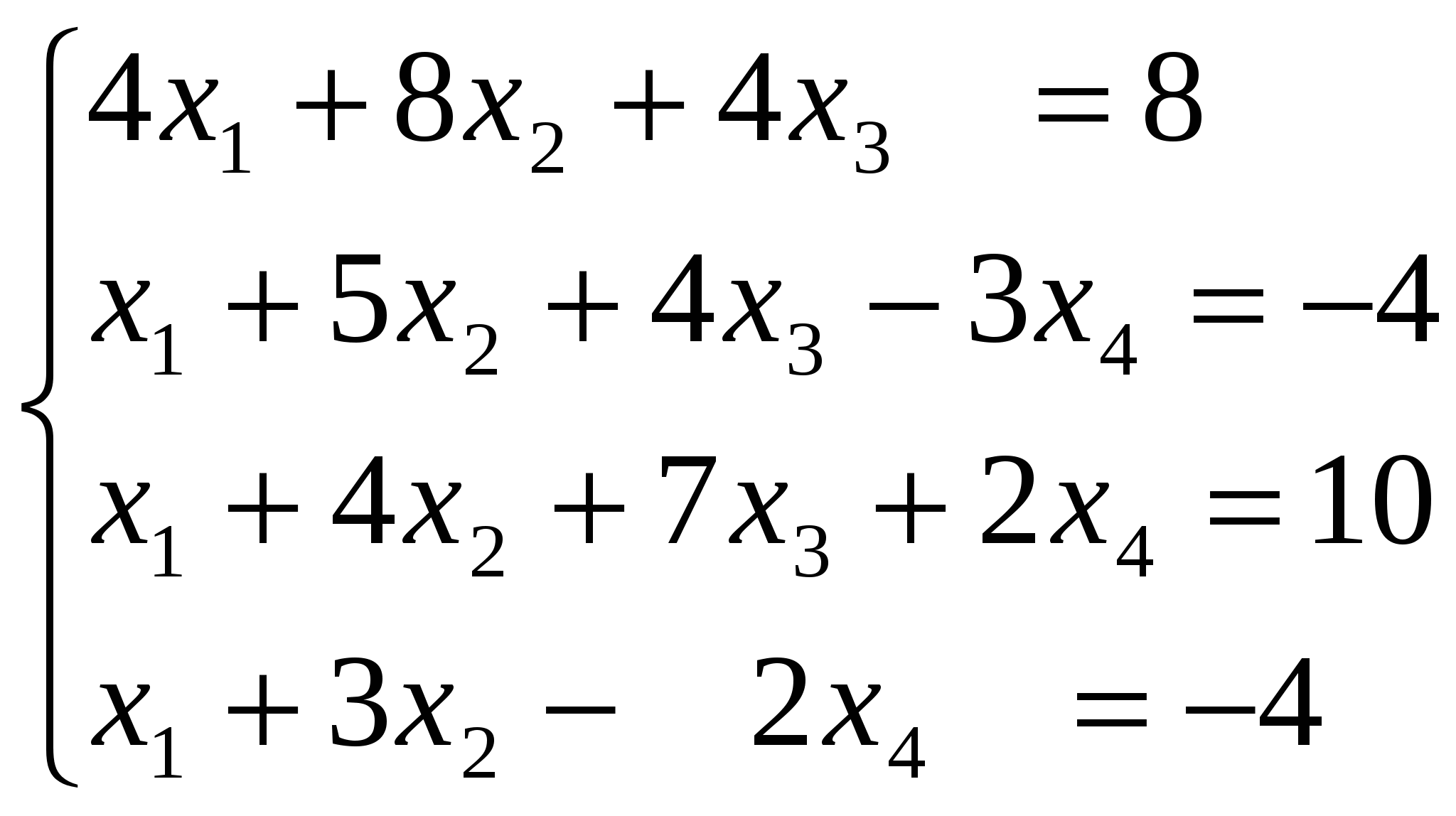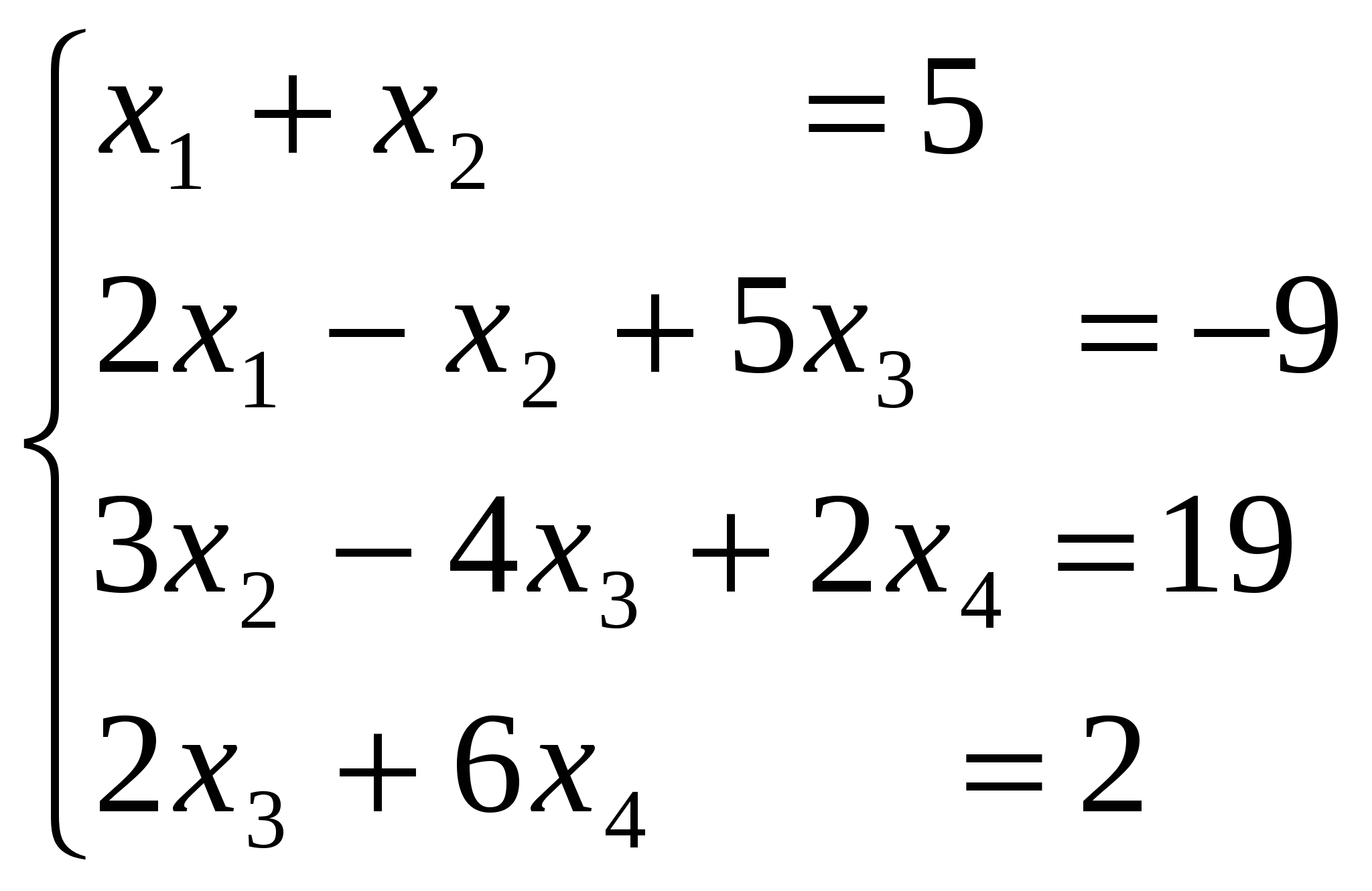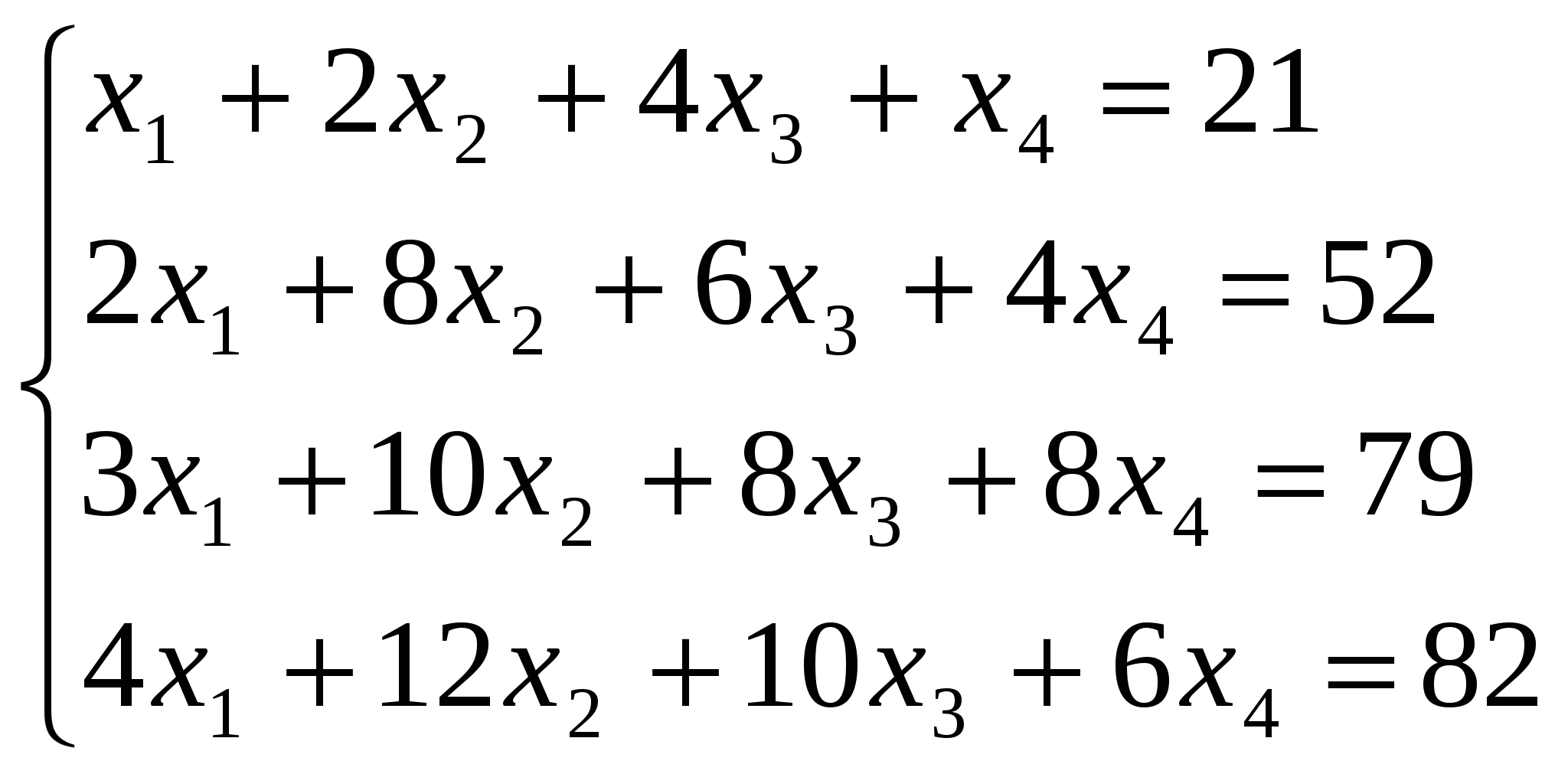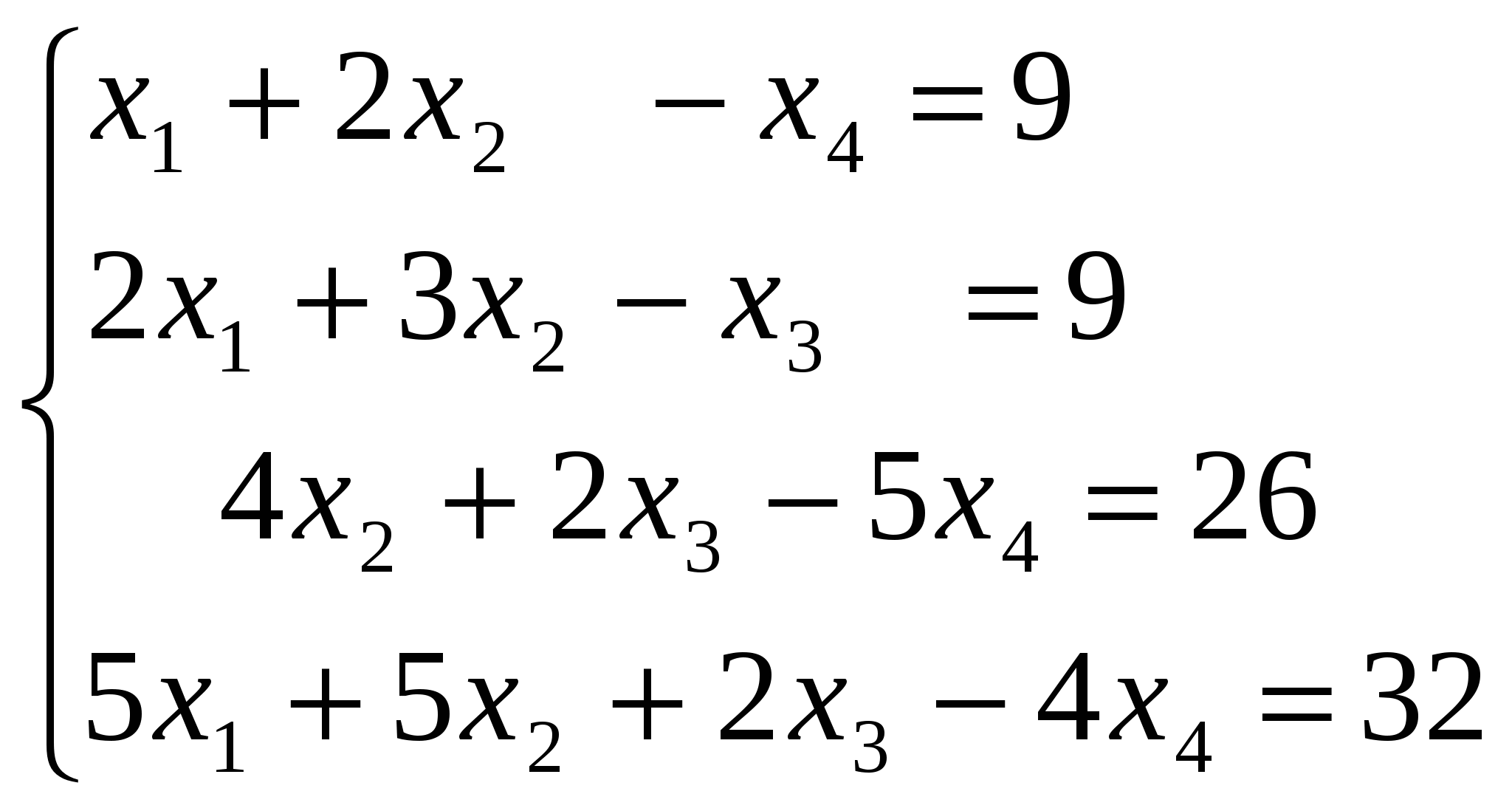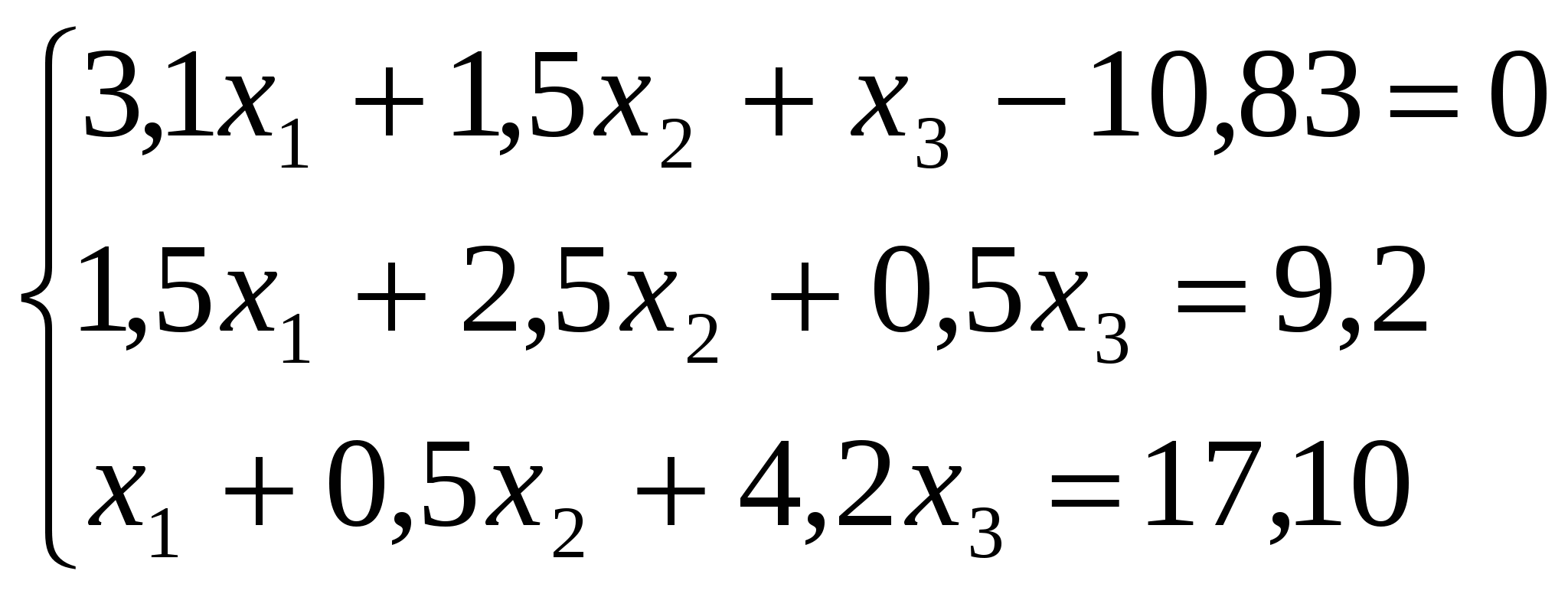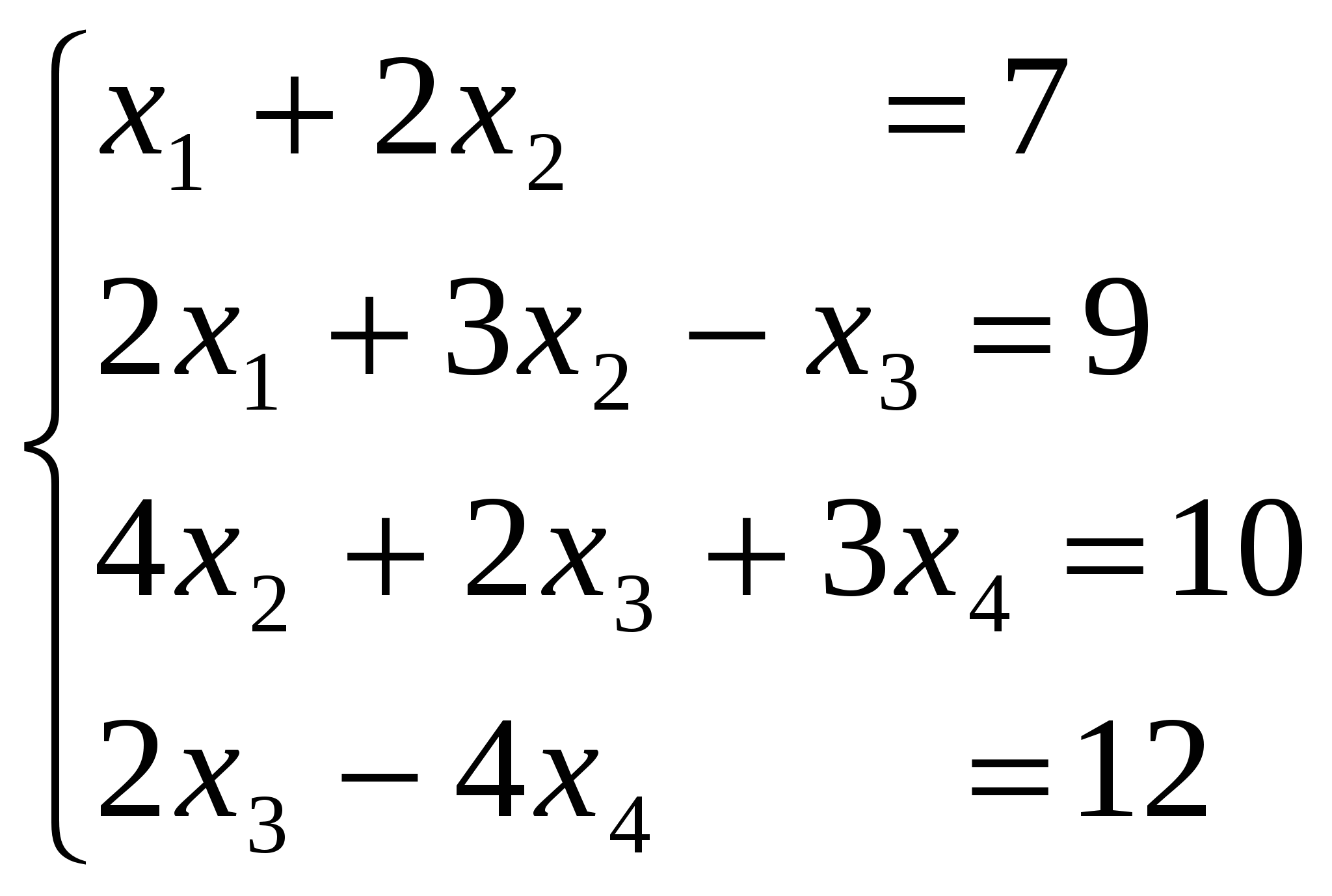Требования к выполнению контрольных работ
по дисциплине “Численные методы”
Номер варианта выбирается по последней цифре зачетной книжки.
Оформление работы допускается как в рукописном, так и в печатном виде.
Формулировки заданий переписываются, все вычисления сопровождаются пояснениями. Результаты вычислений оформляются в виде таблицы
В конце работы должен присутствовать список использованных источников, как бумажных, так и электронных – с полными выходными данными.
Задание 1. Найти значение выражения, используя метод границ
-
Вариант
|
Выражение
|
Значение a
|
Значение b
|
Значение с
|
1
|

|
2,523±0,002
|
7,325±0,003
|
27,32±0,0013
|
2
|
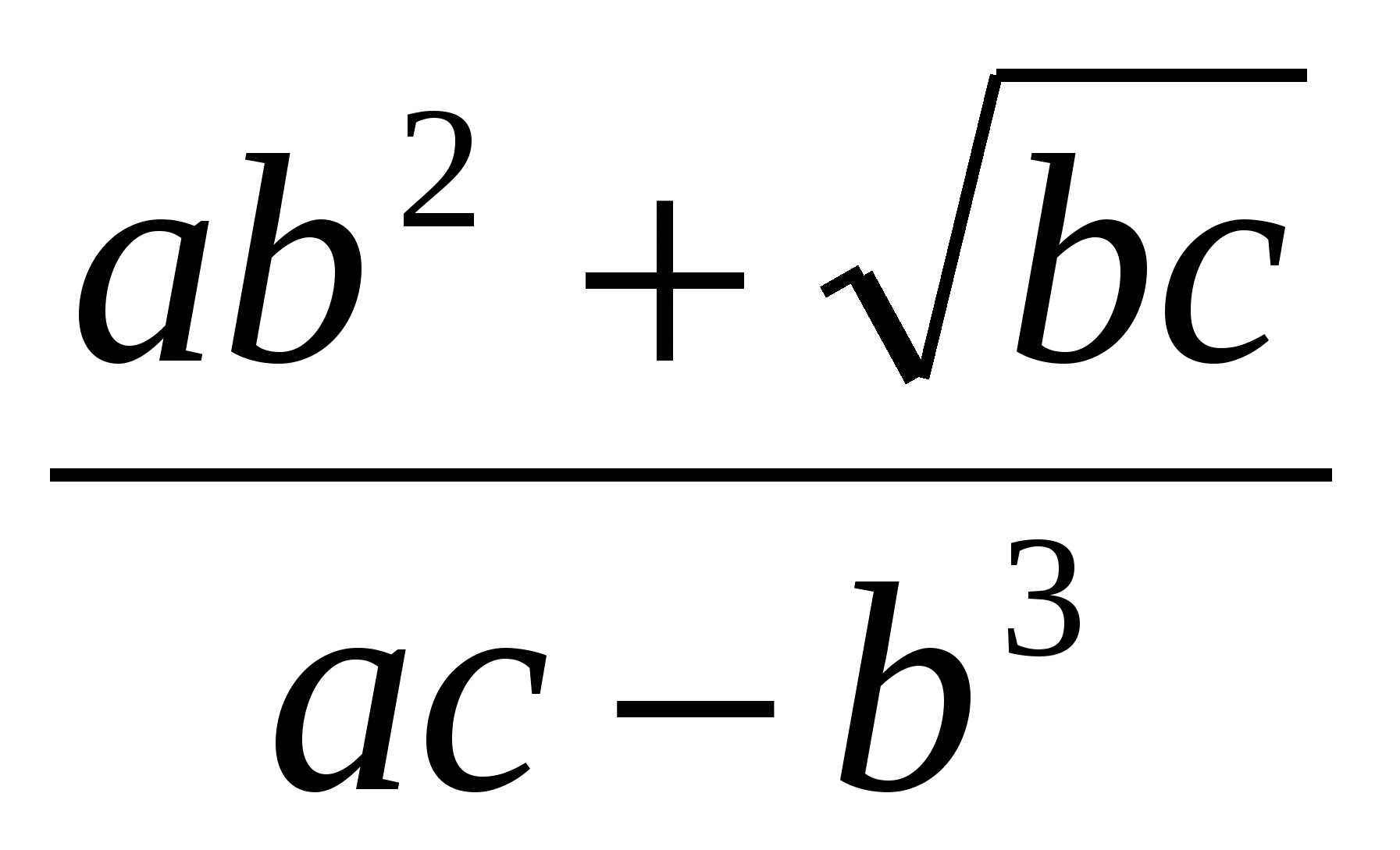
|
0,978±0,002
|
1,21±0,02
|
7,53±0,0012
|
3
|

|
0,927±0,001
|
3,421±0,002
|
16,51±0,0012
|
4
|

|
0,625±0,001
|
4,721±0,006
|
15,21±0,0013
|
5
|
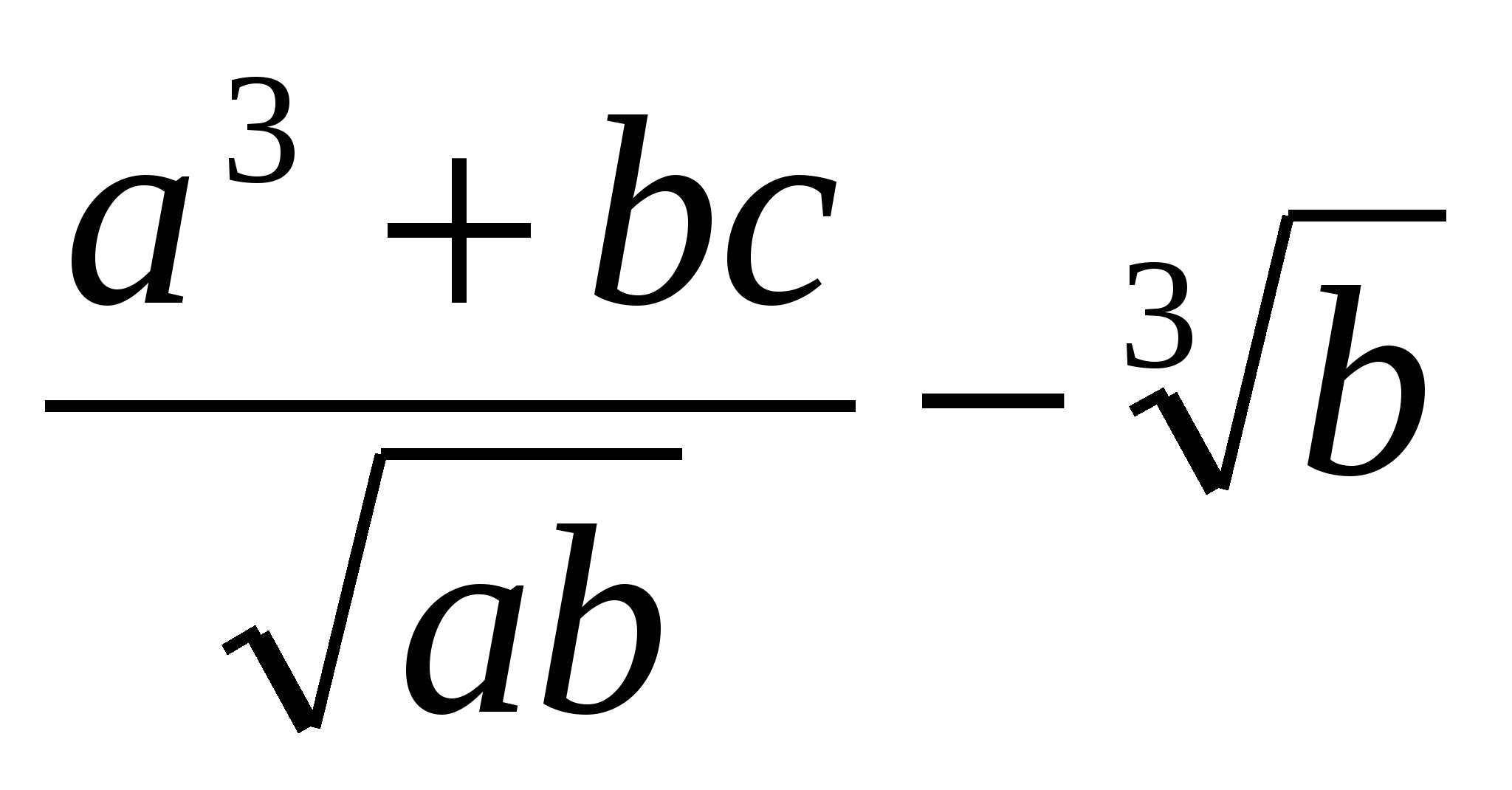
|
3,731±0,002
|
9,343±0,006
|
10,42±0,0012
|
6
|
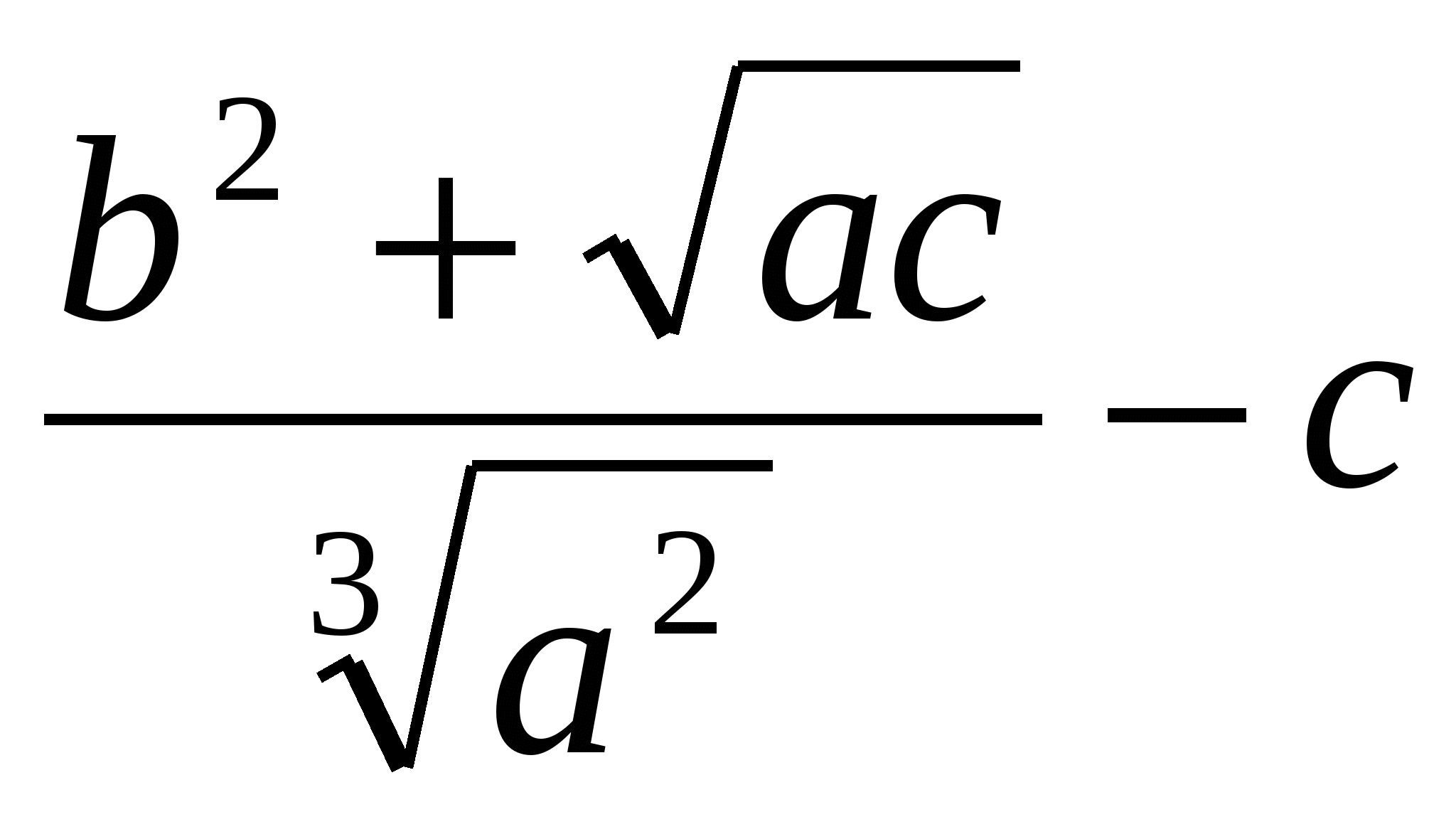
|
9,425±0,003
|
0,442±0,001
|
2,42±0,0011
|
7
|
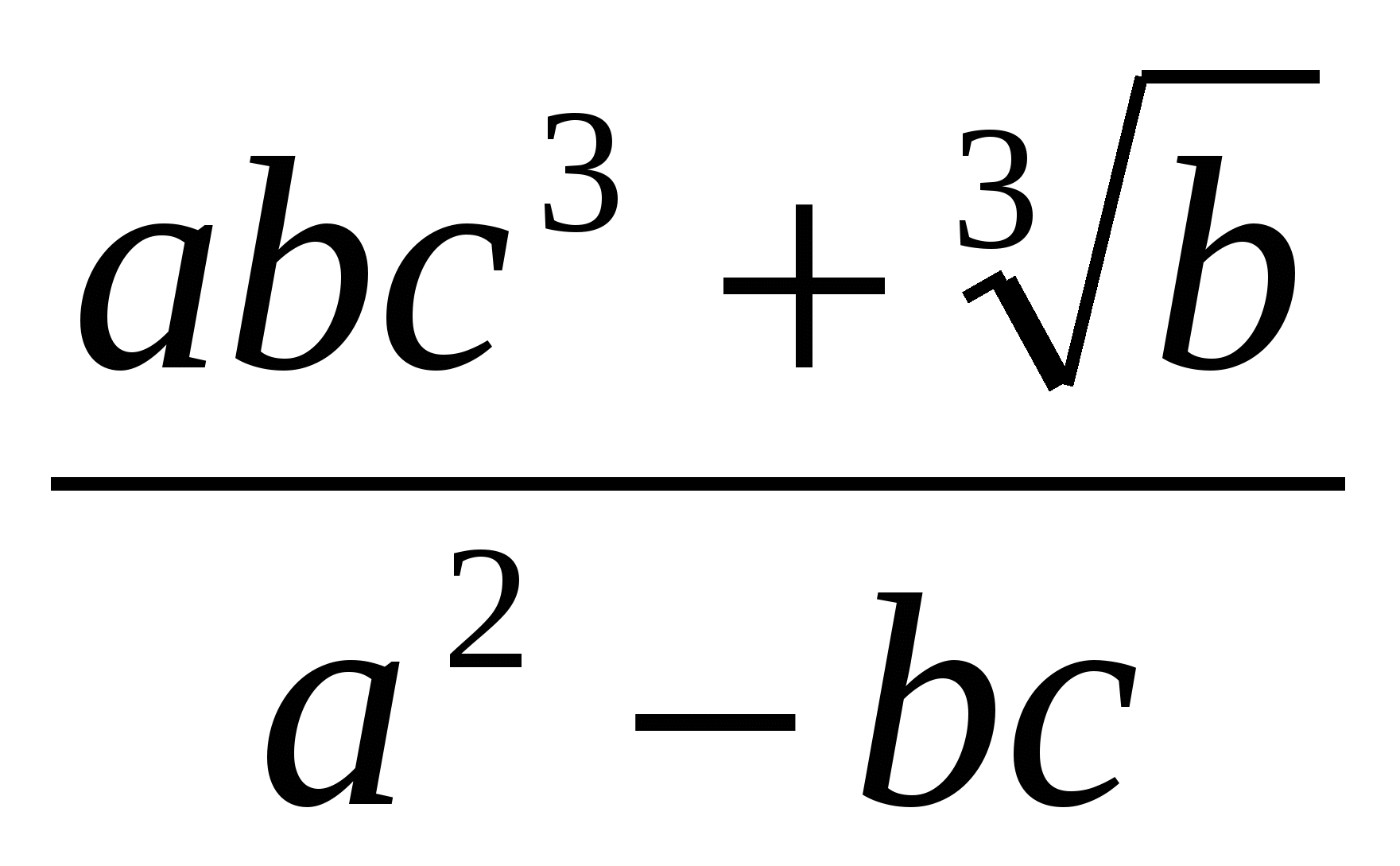
|
4,531±0,004
|
0,723±0,001
|
11,72±0,0012
|
8
|
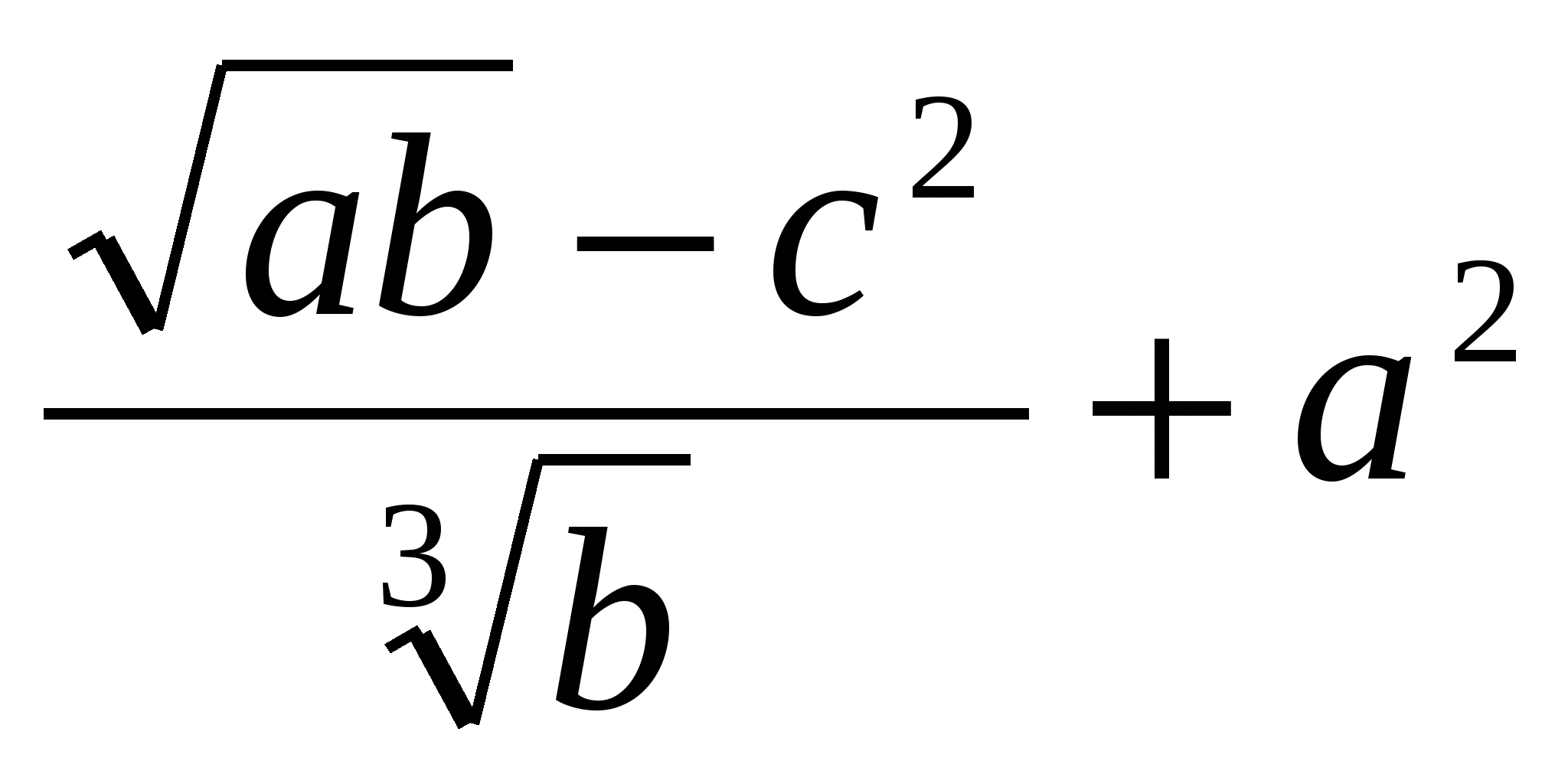
|
3,425±0,005
|
2,41±0,0012
|
10,442±0,006
|
9
|
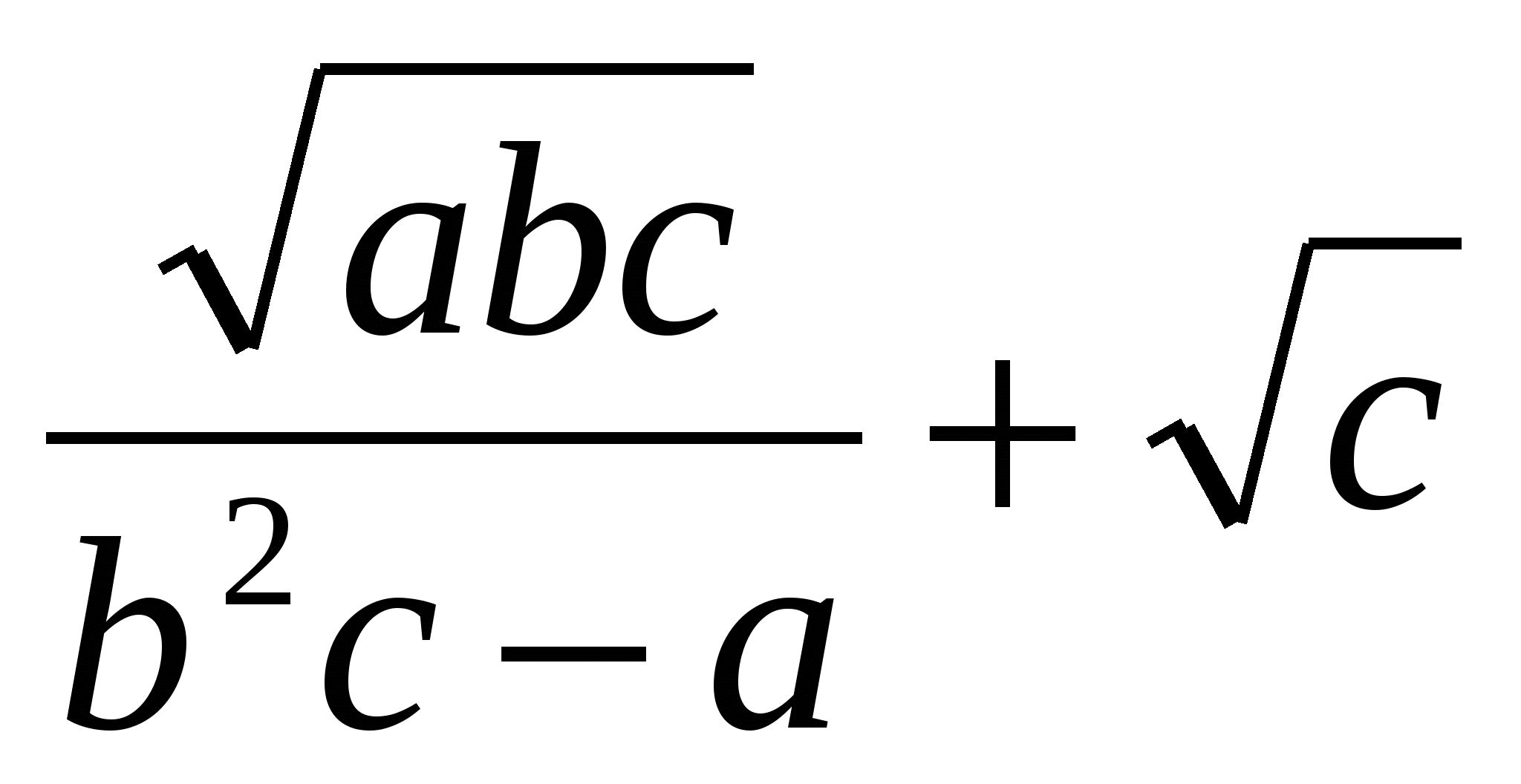
|
2,751±0,002
|
0,893±0,001
|
12,53±0,0014
|
10
|
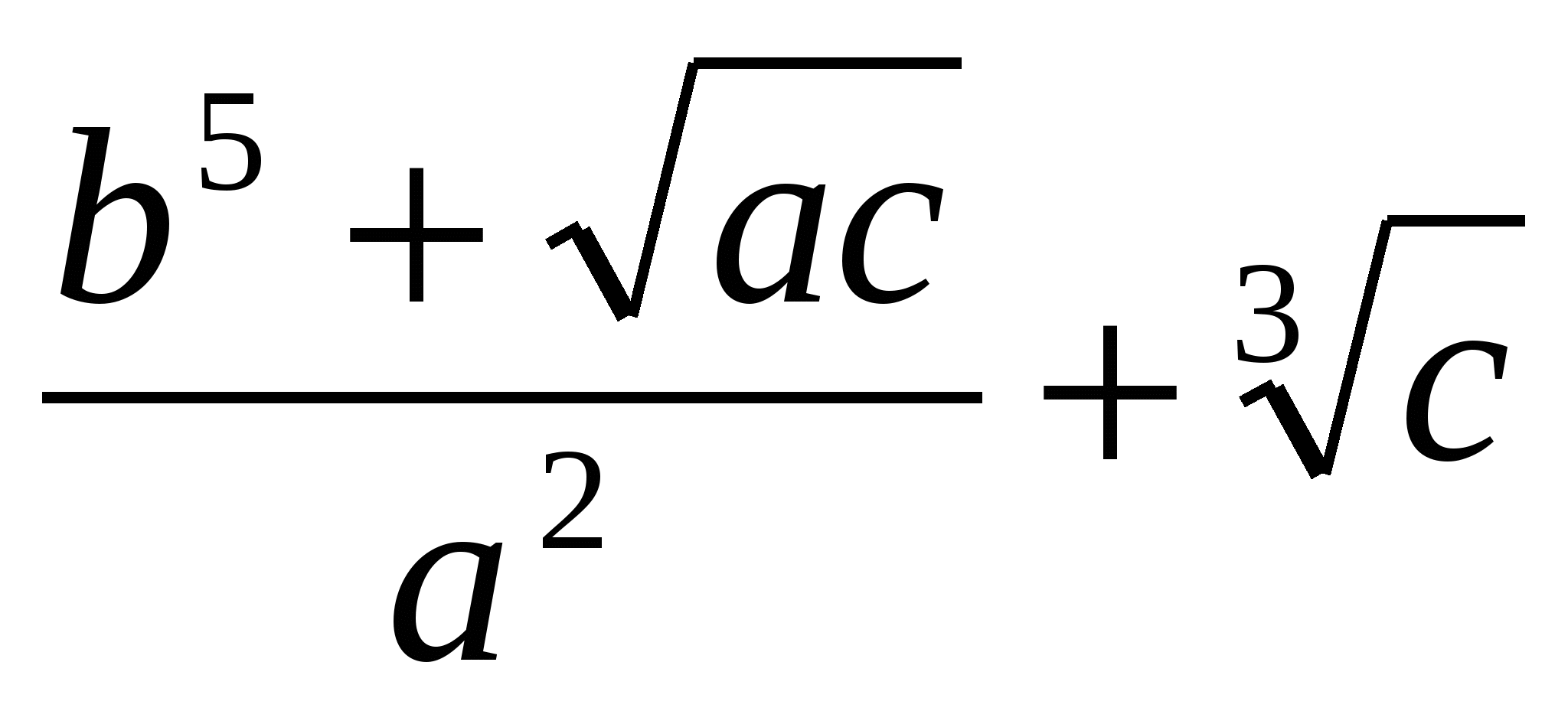
|
1,211±0,005
|
8,721±0,003
|
12,72±0,0011
|
Задание 2. Решить уравнение указанным методом с точностью 10-4
Несмотря на то, что отрезок локализации корня задан, рекомендуется предварительно провести процедуру отделение корней
-
Вариант
|
Уравнение
|
Отрезок локализации
|
Метод
|
1
|
х2 = ех
|
-2 х 2
|
Метод хорд
|
2
|
ln(x) = tg(x)
|
3.5 х 4.5
|
Метод касательных
|
3
|
sin(x) = 2 cos(x)
|
-2 х 2
|
Метод половинного деления
|
4
|
cos(x) +(1+x2)-1 = 0
|
-2 х 2
|
Метод простой итерации
|
5
|
(x-2)2 = ln(x)
|
0.5 х 4.5
|
Метод хорд
|
6
|
ln(x) = 4 – x2
|
1 х 2
|
Метод касательных
|
7
|
x5 + 2x = 8
|
1 х 1.5
|
Метод половинного деления
|
8
|
ln(x) = cos(x)
|
1 х 1.5
|
Метод простой итерации
|
9
|
cos(x) = sin(x2)
|
1 х 2
|
Метод хорд
|
10
|
sin(x) = cos(x2)
|
0.7 х 0.8
|
Метод касательных
|
Задание 3. Решить систему линейных алгебраических уравнений методом Зейделя.
-
Задание 4. Вычислить значение определенного интеграла по формуле трапеций и формуле Симпсона. Методом двойного просчета оцените точность вычислений.
1.  2. 2. 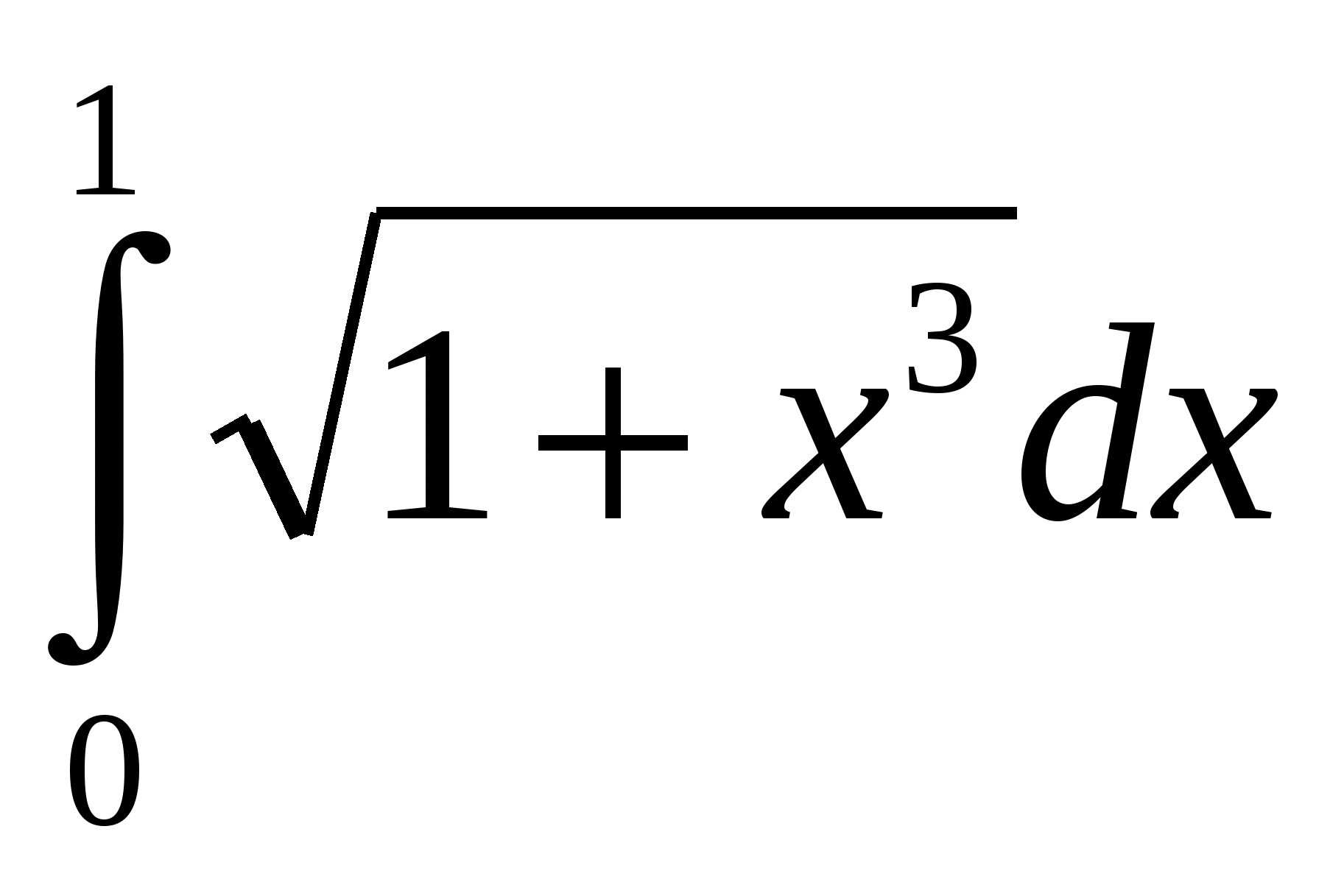
3. 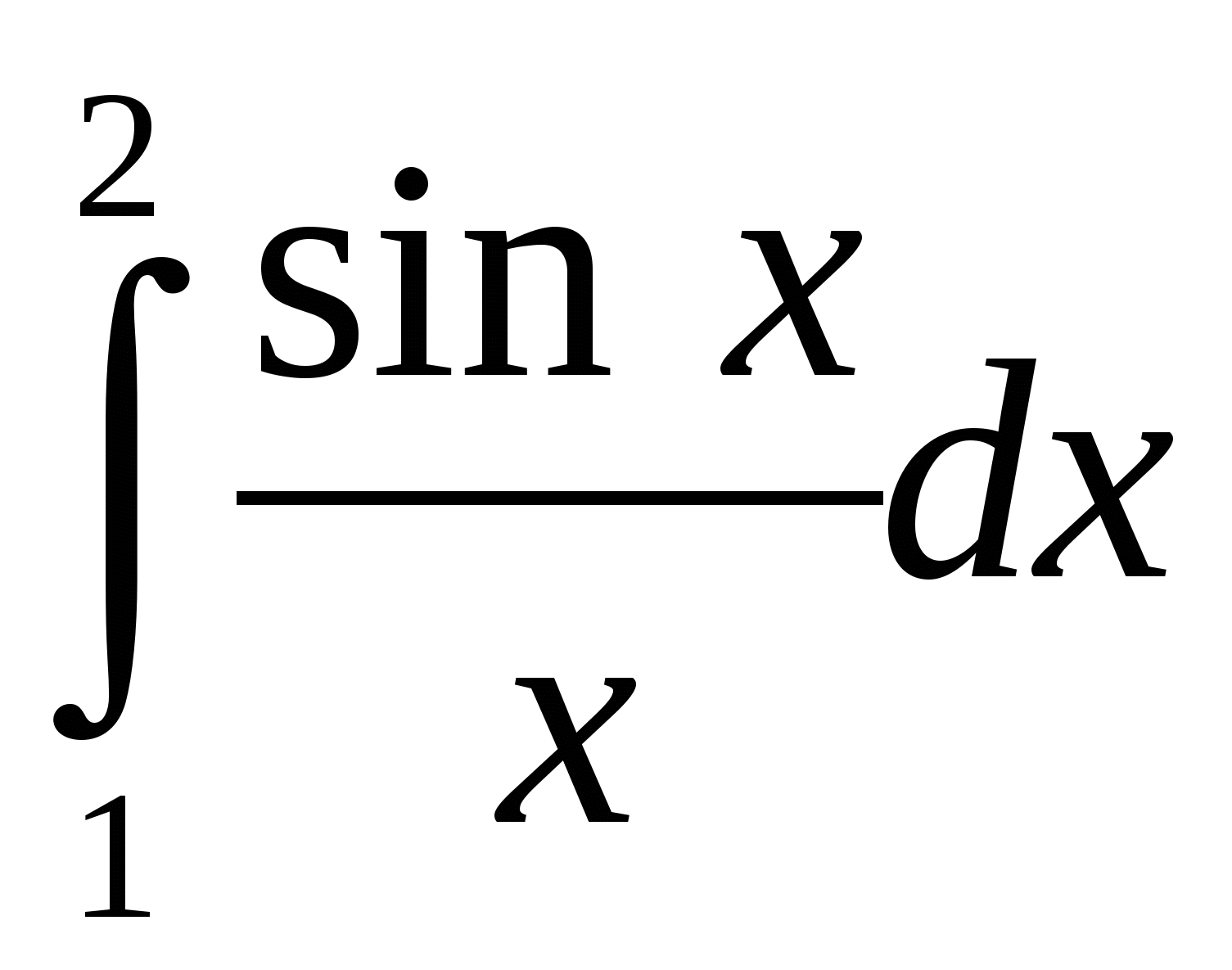 4. 4. 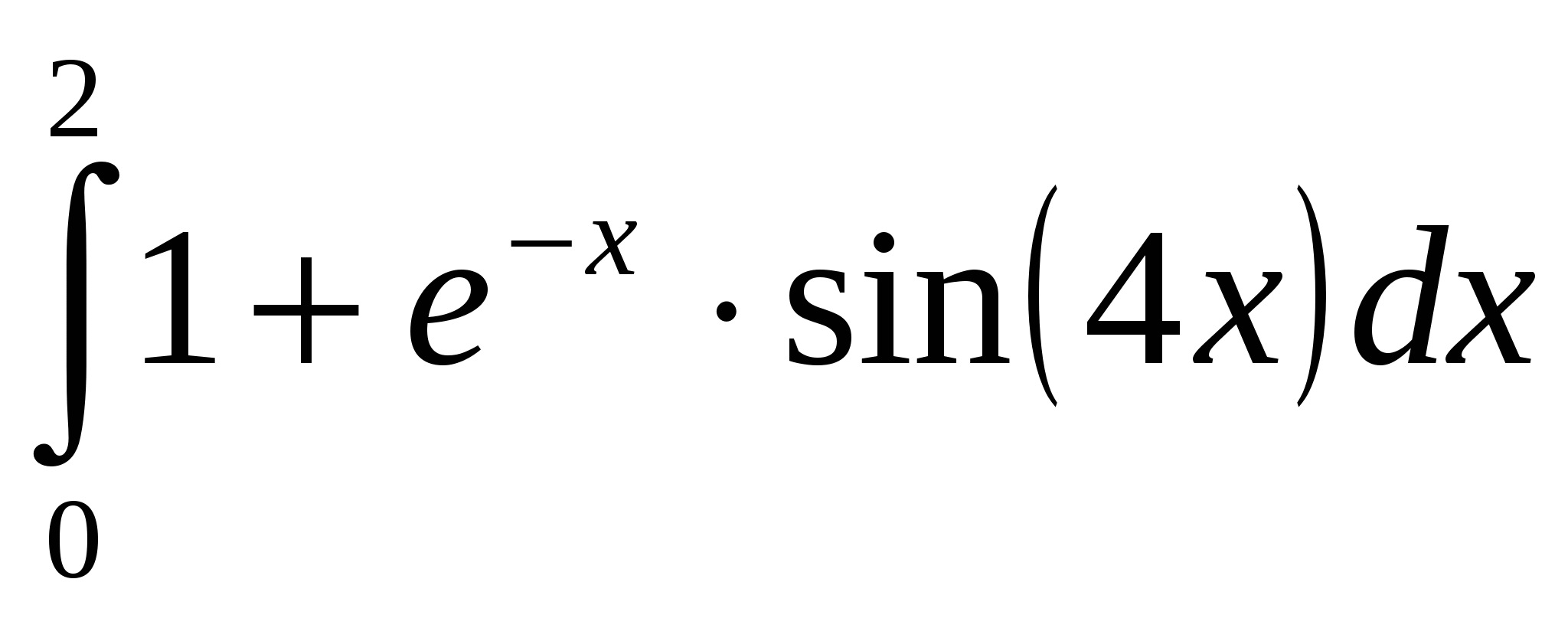
5.  6. 6. 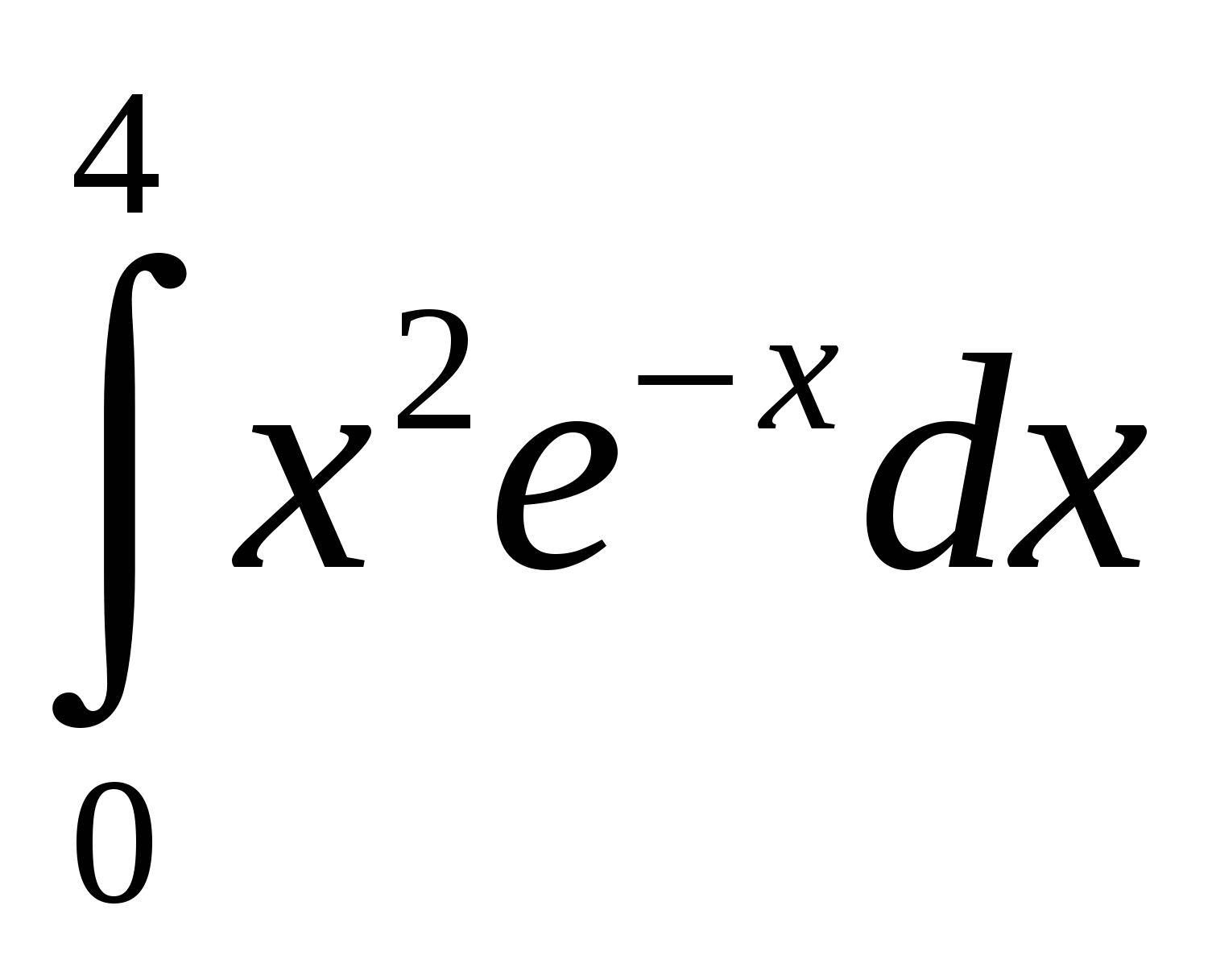
7. 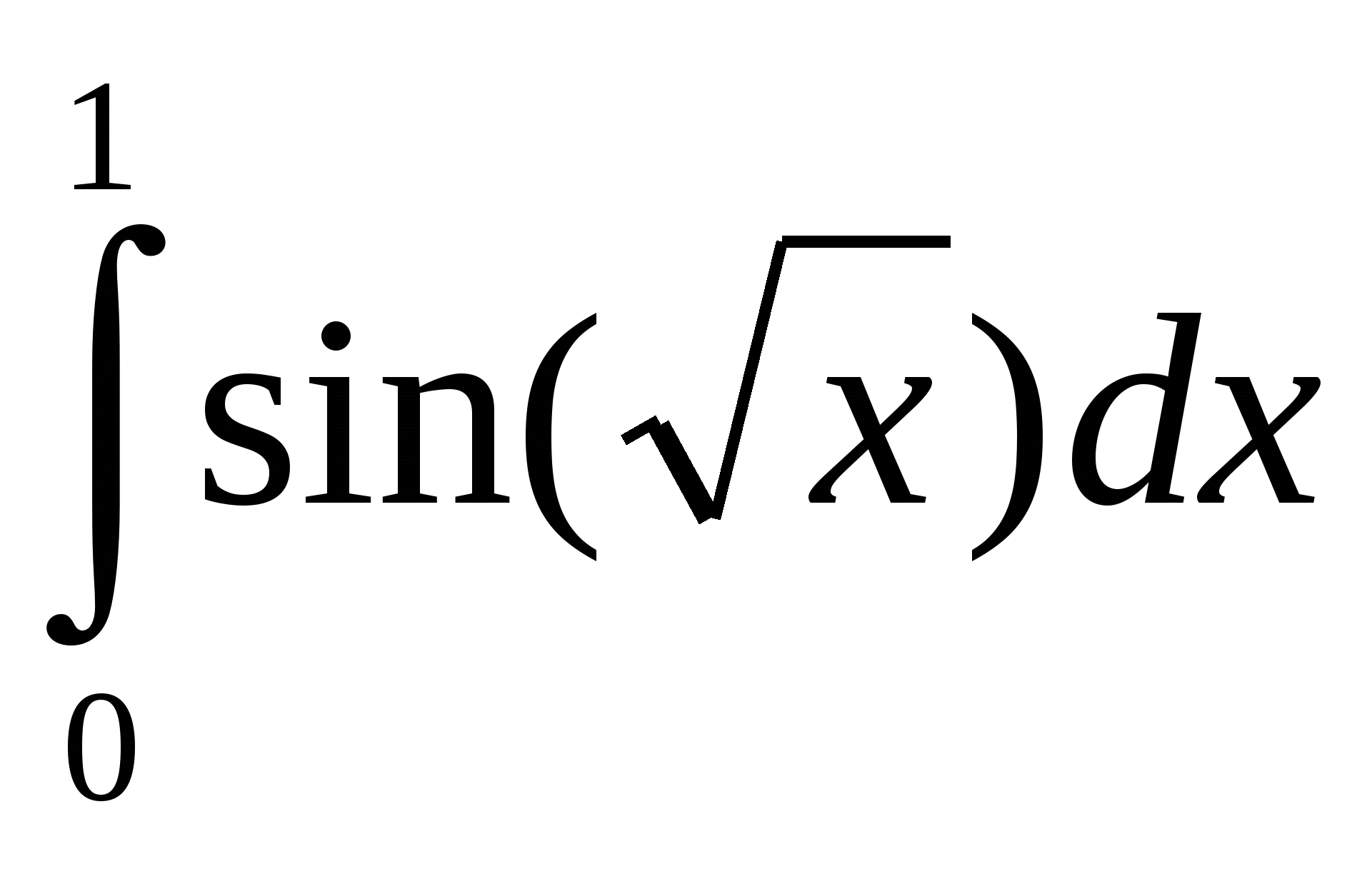 8. 8. 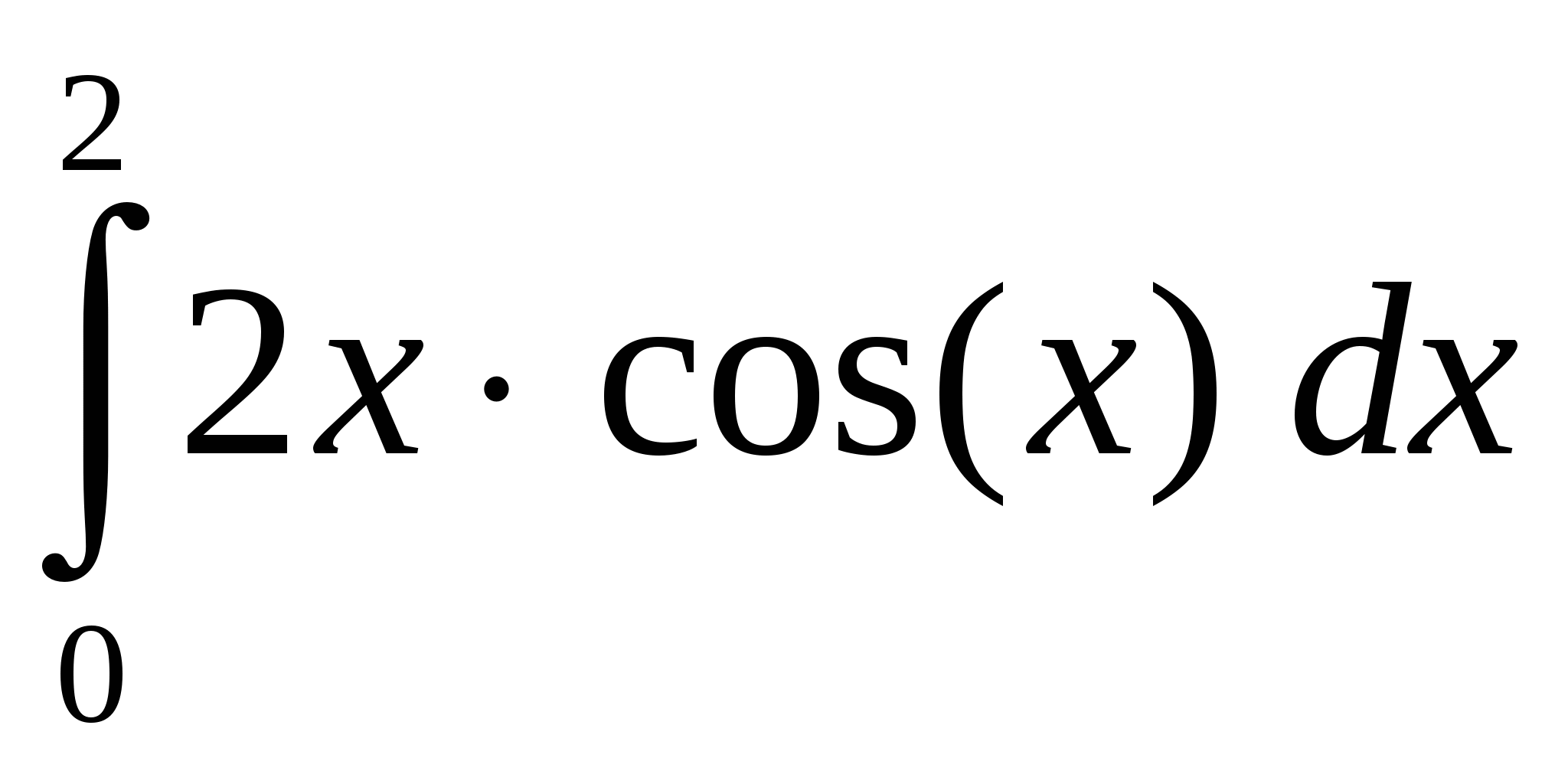
9.  10. 10. 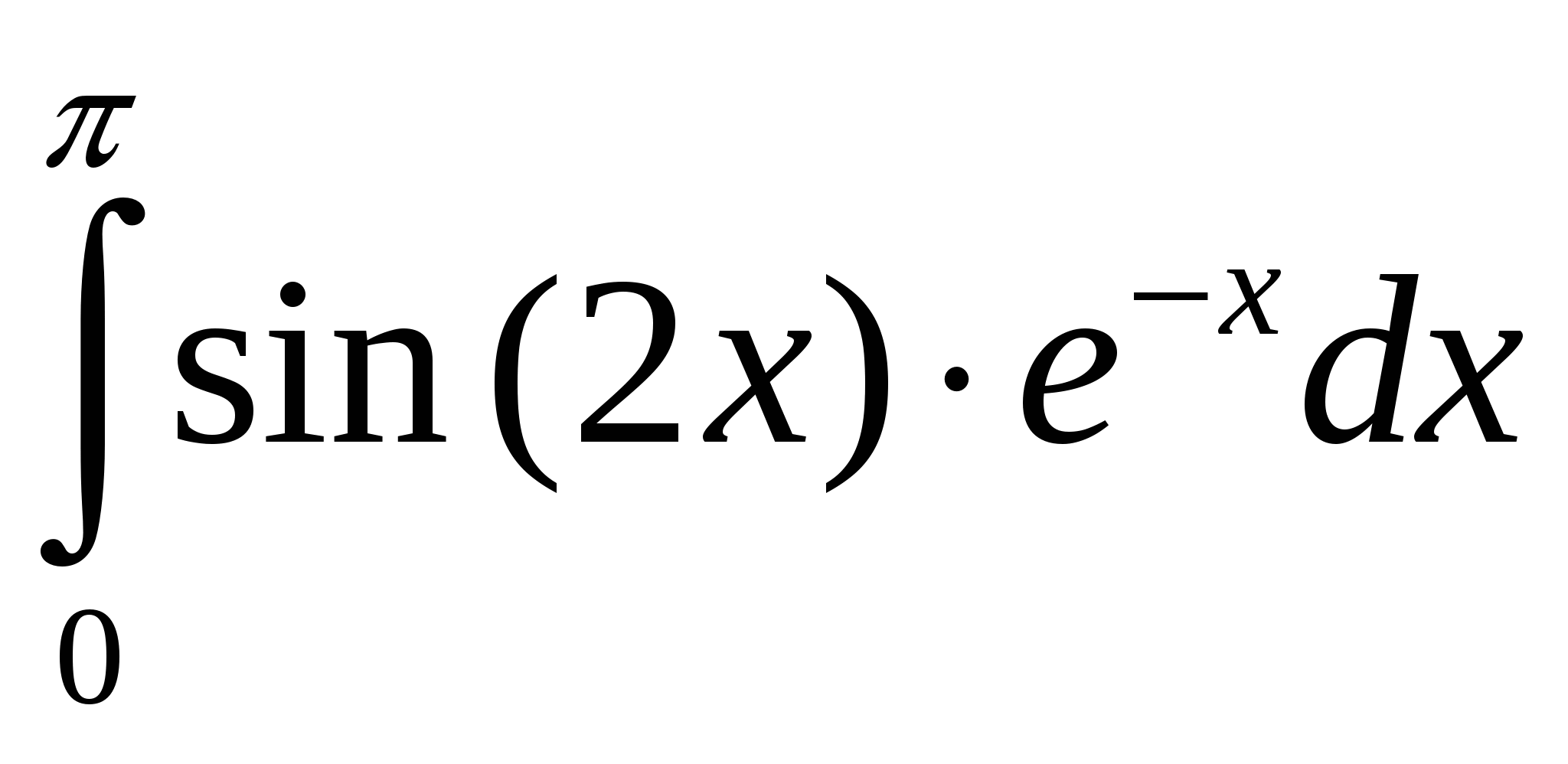
Задание 5. Решить задачу Коши методом Эйлера.
Вариант
|
Дифференциальное уравнение
|
Начальные условия
|
Интервал
|
1
|
Y' = (1-y2)1/2
|
Y(0) = 0
|
[0; /4]
|
2
|
Y' = (x-y)/2
|
Y(0) = 1
|
[0;3]
|
3
|
Y' = 0.12*y
|
Y(0) = 1000
|
[0; 5]
|
4
|
Y' = 0.02*y
|
Y(0) = 5000
|
[0; 5]
|
5
|
Y' = 32-0.032*y3/2
|
Y(0) = 0
|
[0;6]
|
6
|
Y' = 0.00003*y*(25000-y)
|
Y(0) = 250
|
[0; 60]
|
7
|
Y' = x2 - y
|
Y(0) = 1
|
[0; 5]
|
8
|
Y' = y=3*x-x2
|
Y(0) = 1
|
[0; 5]
|
9
|
Y' = -x/y
|
Y(1) = 1
|
[1; 1.4]
|
10
|
Y' = 2*x*y2
|
Y(0) = 1
|
[0; 0.95]
| |
 Скачать 118.5 Kb.
Скачать 118.5 Kb. 2.
2.