2 вариант кванты. Что такое волновая функция Требования, которым отвечает волновая функция

• Название: Что такое волновая функция Требования, которым отвечает волновая функция
• Дата: 16.10.2021
• Размер: 105.98 Kb.
• Имя файла: 2 вариант кванты.docx
• Тип: Документы; #248754

1. 
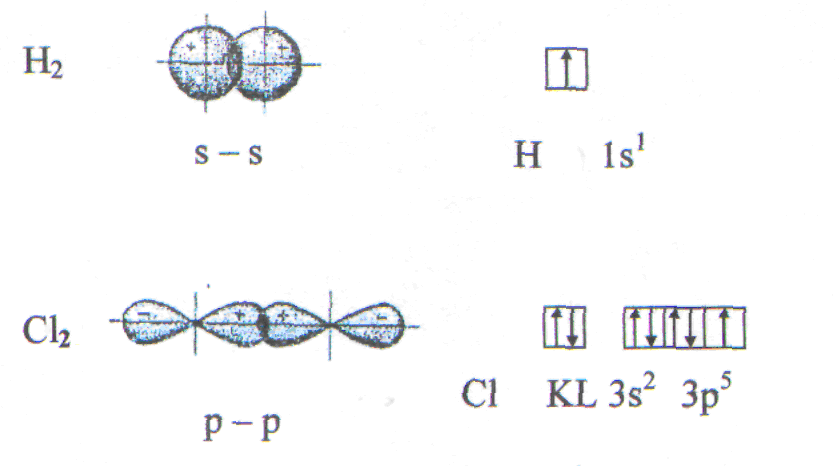
   Что такое волновая функция? Требования, которым отвечает волновая функция
   

Каждое состояние системы n частиц

полностью описывается функцией координат

частиц xi и времени t - волновой функцией

(x1, x2, …, xn, t)  ({x},t).

Требования к «идеальной» ВФ

• Конечна

• Однозначна

• Непрерывна и непрерывно

дифференцируема

• Нормирована

<| >  * rrdr 1

ВФ – функция координат всех частиц системы

и времени:

 (x1 , y1 ,z1 ,...,xn , yn ,zn ,t) (r1 ,...,rn ,t) (r ,t)

Если временной зависимости нет:

 (x1 , y1 ,z1 ,...,xn , yn ,zn ) (r1 ,...,rn ) (r)

2. 
   Запишите выражение для электронной волновой функции в приближении центрального поля. Поясните смысл входящих в него величин.
   

Потенциал 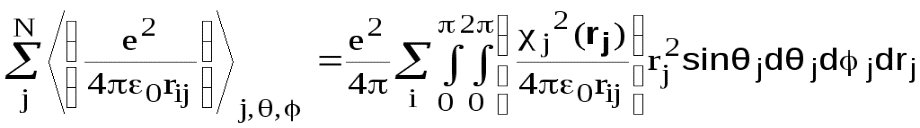  в (40) только в частных случаях (положительные одноэлектронные ионы, атомы инертных газов, атомы N, P и т.д.) является сферически симметричным, т.е. не зависит от углов  и  в сферической системе координат. Однако учет асферичности не улучшает заметно результат расчета. Поэтому обычно используют дополнительное усреднение потенциала в (40), интегрируя его по углам  и :

.

Это - приближение центрального поля: оно позволяет рассматривать ССП-решения для любого атома как модифицированные решения для одноэлектронного водородоподобного атома с потенциалом  .В этом случае потенциальная энергия зависит только от расстояния до ядра, т.е. сила притяжения к ядру носит центральный характер. Поэтому угловой момент электрона относительно ядра постоянен, а волновая функция является собственной функцией не только гамильтониана, но и операторов квадрата углового моментаL² и его проекции L_z . Тогда переменные в уравнении Шредингера в сферических координатах разделяются и волновые функции, описывающие состояния электронов атома в r-пространстве (атомные орбитали), имеют вид:

(r) = N(n,l) R_n,l ( r )Y_lm­ (,  ),

+где N(n,l) - нормировочный множитель, R_n,l ( r ) - радиальная функция, Y_lm­ (,  ) - угловая функция; n, l и m – главное, орбитальное и магнитное квантовые числа, соответственно.

3. 
   Приведите примеры эффективного (S ij>0) перекрывания атомных орбиталей s- , p- , d- типа при образовании химической связи
   

а) Положительное (эффективное) перекрывание. В области перекрывания волновые функции обоих электронов ( a и b) имеют одинаковый знак. При положительном перекрывании растет электронная плотность в зоне перекрывания и происходит образование связи.

4. 
   Запишите условие нормировки волновой функции.
   

Вероятность обнаружить частицу во всем бесконечном пространстве равна единице. Отсюда следует условие нормировки волновой функции:

 

Величина   является плотностью вероятности, или, что то же самое, плотностью распределение координат частиц